大学物理上复习总结 24页

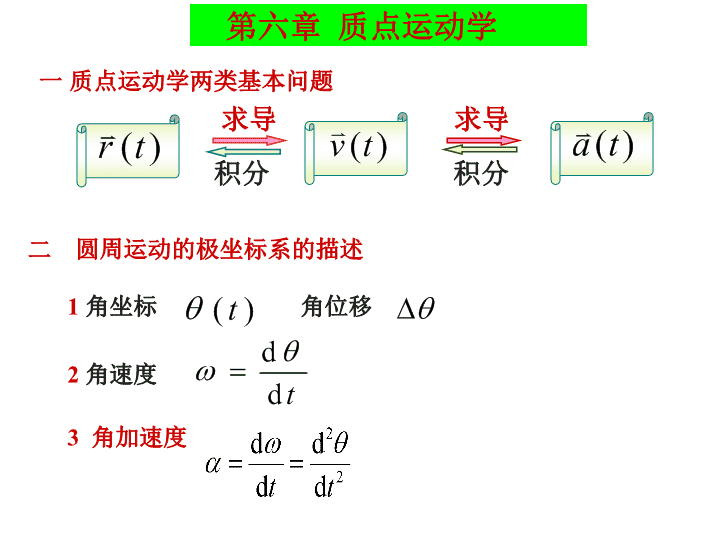
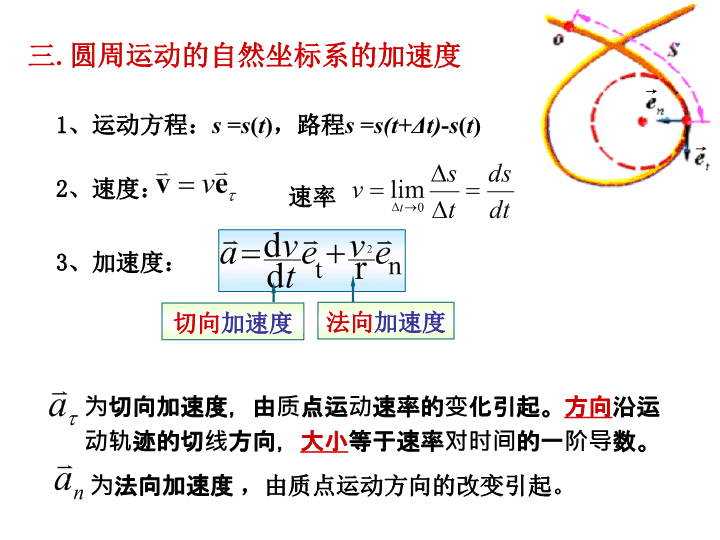
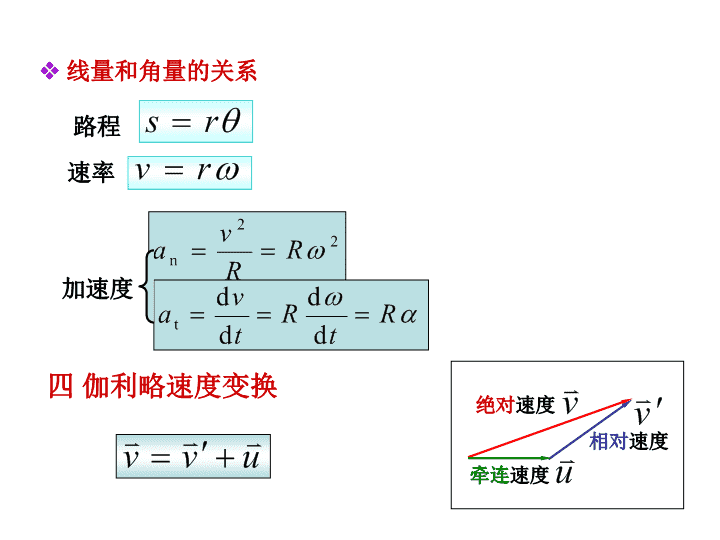
求导求导积分积分一质点运动学两类基本问题第六章质点运动学二圆周运动的极坐标系的描述1角坐标角位移2角速度3角加速度\n三.圆周运动的自然坐标系的加速度1、运动方程：s=s(t)，路程s=s(t+Δt)-s(t)2、速度：速率3、加速度：为切向加速度，由质点运动速率的变化引起。方向沿运动轨迹的切线方向，大小等于速率对时间的一阶导数。为法向加速度，由质点运动方向的改变引起。法向加速度切向加速度\n四伽利略速度变换绝对速度牵连速度相对速度速率线量和角量的关系加速度路程\n第七章质点动力学一、牛顿运动定律二、动量冲量动量定理动量守恒定律动量瞬时量冲量（矢量）过程量动量定理若质点系所受的合外力当时，可近似地认为系统总动量守恒．动量守恒定律则系统的总动量不变，则\n三、功动能定理保守力：如果力所做的功与路径无关，而只决定于物体的始末相对位置，这样的力称为保守力。四、保守力势能势能：质点在保守力场中某点的势能，在量值上等于质点从M点移动至零势能点M0的过程中保守力所作的功。\n五机械能守恒定律当时，有——只有保守内力作功的情况下，质点系的机械能保持不变．\n1.力矩大小：方向：由右手螺旋定则确定在定轴转动中，力矩的方向是沿着转轴的。3.转动定律2.转动惯量第八章刚体力学一力矩转动惯量转动定理\n◆应用转动定律求解定轴转动问题的一般步骤：（1）隔离物体（对象）；（2）对作平动的物体进行受力分析，应用牛顿第二定律列方程；对作转动的物体进行受力矩分析，应用转动定律列方程；（3）建立平动与转动之间的联系；如：（4）联立求解。\n对比：2、力矩对时间的积累效应——角动量定理2.角动量定理1.冲量矩：3、角动量守恒定律刚体绕定轴转动的角动量：1、角动量(动量矩):或积分形式：或对比冲量:对比动量定理:若M=0，则L=常量或对比动量定理:微分形式:二角动量角动量定理角动量守恒\n101力矩的功力矩的功率2转动动能3刚体绕定轴转动的动能定理绕定轴转动刚体在任一过程中动能的增量，等于在该过程中作用在刚体上所有外力所作功的总和——刚体绕定轴转动的动能定理三力矩的功转动动能定理\n（1）简谐运动的动力学方程（2）简谐运动的运动学方程弹簧振子一、简谐运动的方程和特征第九章机械震动\n二描述简谐振动的物理量1振幅2周期、频率弹簧振子周期周期频率圆频率3相位初相位对给定振动系统，周期由系统本身性质决定，振幅和初相由初始条件决定.\n自Ox轴的原点O作一矢量，使它的模等于振动的振幅A，并使矢量在Oxy平面内绕点O作逆时针方向的匀角速转动，其角速度与振动频率相等，这个矢量就叫做旋转矢量.三简谐运动的矢量图示法以为原点旋转矢量的端点在轴上的投影点的运动为简谐运动.\n1动能(以弹簧振子为例)四简谐运动的能量2势能3机械能守恒\n五两个同方向同频率简谐运动的合成两个同方向同频率简谐运动合成后仍为同频率的简谐运动加强减弱（1）相位差（2）相位差\n16一描述波动的物理量（波长周期频率波速）波传播方向上相邻两振动状态完全相同的质点间的距离（一完整波的长度）.或在波得传播方向上相位差为2π的振动质点之间的距离。如果从波得传播角度来定义，是一个周期内某振动状态（相位）传播的距离。波长描述了波得空间周期性。1波长2周期T波向前传播一个波长所需的时间，或一完整波通过波线上某点所需的时间.3频率单位时间内波向前传播的完整波的数目.（1内向前传播了几个波长）。一般情况下，振动在媒质中传播时频率不变，所以就等于波源的振动频率，自然波的周期也等于波源的振动周期。决定于介质的性质（弹性模量和密度）某一振动状态（相位）单位时间内传播的距离。4波速第10章机械波\n二.平面简谐波的波方程（1）导出波方程的思路◆已知波源的振动方程，当振动传到各质元时，各质元都以相同的振幅、频率来重复波源的振动。◆波源的振动状态以某一速度先后传播到各个质元，沿波的传播方向上的各质元振动的相位依次落后。（2）导出波方程步骤◆选定坐标并明确波的传播方向。◆给出波的传播方向上某点(参考点、波源)的振动方程。◆比较位于x处的任一点和参考点相位的超前和落后关系，由参考点的振动表达式即可得出波的表达式。\n可得波动方程的几种不同形式：质点的振动速度，加速度\n第11章气体动理论\n\n12章热力学基础\n热力学第一定律的应用\n热力学第一定律的应用\n