《大学物理习题》ppt课件 18页

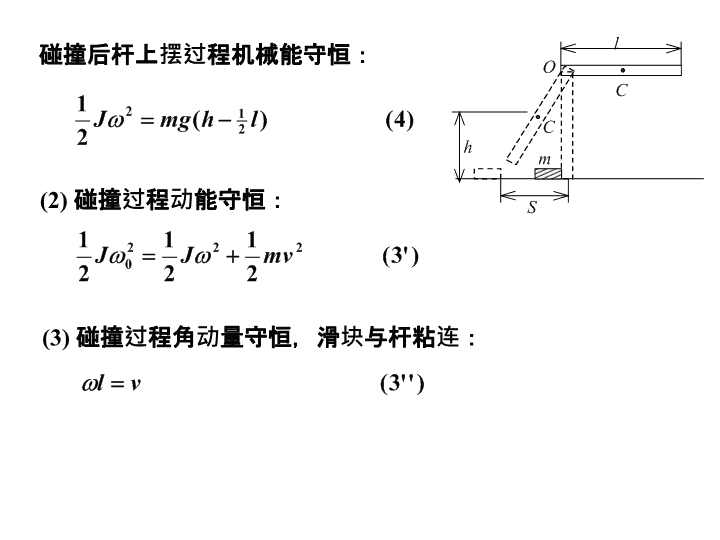
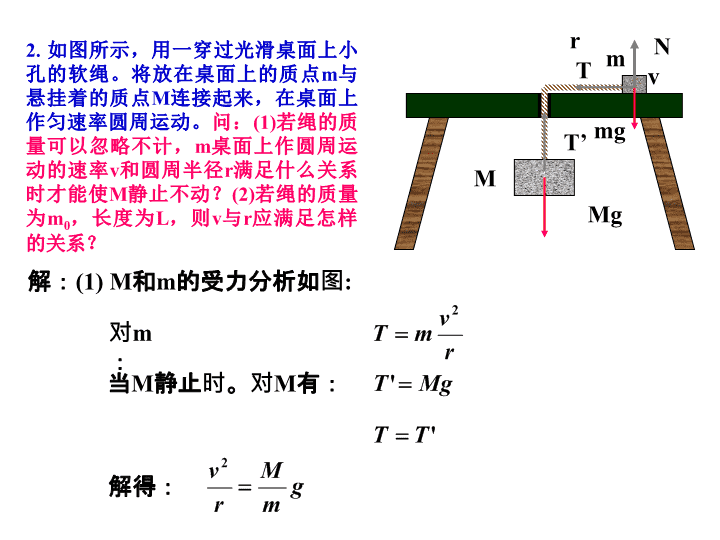
1.如图所示，一均匀细棒，长为l，质量为m，可绕过棒端且垂直于棒的光滑水平固定轴O在竖直平面内转动。棒被拉到水平位置从静止开始下落，当它转到竖直位置时，与放在地面上一静止的质量亦为m的小滑块碰撞，碰撞时间极短。小滑块与地面间的摩擦系数为μ，碰撞后滑块移动距离S后停止，而棒继续沿原转动方向转动，直到达到最大摆角。求：(1)碰撞后棒的中点C离地面的最大高度h。(2)若碰撞为完全弹性碰撞，h=?(3)若碰撞为完全非弹性碰撞，h=?解：(1)碰撞前杆的转速：碰撞过程角动量守恒：针对小滑块用动能定理：\n碰撞后杆上摆过程机械能守恒：(2)碰撞过程动能守恒：(3)碰撞过程角动量守恒，滑块与杆粘连：\n2.如图所示，用一穿过光滑桌面上小孔的软绳。将放在桌面上的质点m与悬挂着的质点M连接起来，在桌面上作匀速率圆周运动。问：(1)若绳的质量可以忽略不计，m桌面上作圆周运动的速率v和圆周半径r满足什么关系时才能使M静止不动？(2)若绳的质量为m0，长度为L，则v与r应满足怎样的关系？mMrvmgNT’MgT解：(1)M和m的受力分析如图:对m：当M静止时。对M有：解得：\n(2)若绳的质量不为0，则作圆周运动的绳也需要向心力，设绳的线密度为λ=m0/L距离圆心x处的长度为dx的一段绳质量为dm=λdx在水平方向上有：积分得：竖直绳的力平衡再代入T和T’，整理得dmTxT’xTxT’’T’’Mg(L-r)gT’xo\n3.如图：空心环B半径R，初始角速度ω0，对轴转动惯量为J0，可绕转轴自由旋转。求：小球A无摩擦滑到θ角时，环的角速度和球相对于环的速度各为多少？w0bO'RBAOacθ解：小球下落过程，球与环组成的系统对轴OO’角动量守恒：aθ:小球A在θ点的速率为下滑过程中，小球、环、地球为系统机械能守恒：aθ:\n4.长为l，质量为m的均匀杆，在光滑桌面上由竖直位置自然倒下，当夹角为θ时（见图），求：(1)质心的速度；(2)杆的角速度。解：(1)水平方向不受力，故质心在水平方向不产生加速度，质心原来静止，故质心水平方向的速度为零。只有竖直方向的速度。设任一时刻，质心的位置为：则：\n(2)在杆下滑过程中，只有重力作功，故机械能守恒，对任一夹角，有：由于：代入后:经整理，得：\n5.质量很小长度为l的均匀细杆，可绕过其中心O并与纸面垂直的轴在竖直平面内转动。当细杆静止于水平位置时，有一只小虫以速率v0垂直落在距点O为l/4处，并背离点O向细杆的端点A爬行。设小虫与细杆的质量均为m。问：欲使细杆以恒定的角速度转动，小虫应以多大速率向细杆端点爬行?解：小虫与细杆的碰撞视为完全非弹性碰撞，碰撞前后系统角动量守恒由角动量定理\n即考虑到\n6.一装沙车以速率v=3m/s从沙斗下通过，每秒钟落入车厢的沙为m=500kg，如果使车厢的速率保持不变，应用多大的牵引力？(设车与轨道的摩擦不计)解：设t时刻已落入车厢沙子的质量与沙车的质量之和为m，dt时间内即将落入的沙子质量为dm。以m和dm为研究系统t+dt时刻的动量为t时刻水平总动量为动量的增量为根据动量定理\n7.如图，斜面固定在地面上，不计所有摩擦，求斜面与A间，A与B间的作用。A木块：牛二律的矢量式的形式投影式(代数式)解：以地面为参照系（惯性系）的受力图A木块：\n取向下为正方向，投影式(代数式）为运动学规律联立求解，运算及结果略。B木块：牛二律的矢量式的形式\n因木块A相对地面加速运动，故为非惯性系，取A木块为参照系，本题也可在非惯性系内求解。在非惯性系内的牛二律形式木块B的受力图为在非惯性系内的牛二律形式此时，木块A的受力图为取向下为正方向，投影式(代数式）为在竖直方向B相对B无运动。计算略。\n8、8、唱机的转盘绕着通过盘心的固定竖直轴转动，唱片放上去后将受转盘摩擦力的作用而随转盘转动,如图3所示。设唱片为半径为R、质量为m的均匀圆盘，唱片和转盘间的摩擦系数为µk，转盘以角速度w匀速转动。求：（1）唱片刚被放到唱盘上去时受到的摩擦力矩为多大？（2）唱片达到角速度w需要多长时间？在这段时间内，转盘保持角速度w不变，驱动力矩共做了多少功？唱片获得了多大的动能？解：唱片的面密度为m/(πR2)。在唱片上取如图8所示的面积元ds，其面积为dS=rdθdr。小质元的质量可以写为dm=mrdθdr/(πR2)\n该面元所受摩擦力对转轴的力矩为：dM=rdf＝µkrdmg＝µkmgr2dθdr/(πR2)唱片上各质元所受的力矩方向相同，所以整个唱片受到的摩擦力矩的大小为（2）唱片受到摩擦力矩作用，做匀角加速转动，角速度增大，直至达到转盘的角速度为止。这段时间内，其角加速度的值由转动定律求得rdrO图8习题8解答用图\n唱片达到角速度w需要的时间为转盘保持角速度w不变，驱动力矩的功为A＝M·Dq＝M·wt＝唱片获得的动能为rdrO图8习题8解答用图θ\n9.质量为m1半径为R水平圆盘绕竖直轴以角速度ω0转动。圆盘上有一质量为m2玩具汽车从t=0时刻沿它的一条半径由中心向边缘行驶，如图9所示。现将玩具汽车视为质点，且它相对于盘的速率v恒定。已知m1=2kg,m2=1kg,R=1m,ωo=20rad/s,v=1m/s，求:玩具汽车行至圆盘边缘时,圆盘转了多少圈?图9习题9用图解圆盘与玩具汽车组成的系统角动量守恒，得到方程解方程得：圆盘转动惯量为\n车在t时刻位于距轴r处时的转动惯量为圆盘在0→t时间间隔内的角位移为将已知条件代入上式得:圆盘在0→t时间间隔转动的圈数N为