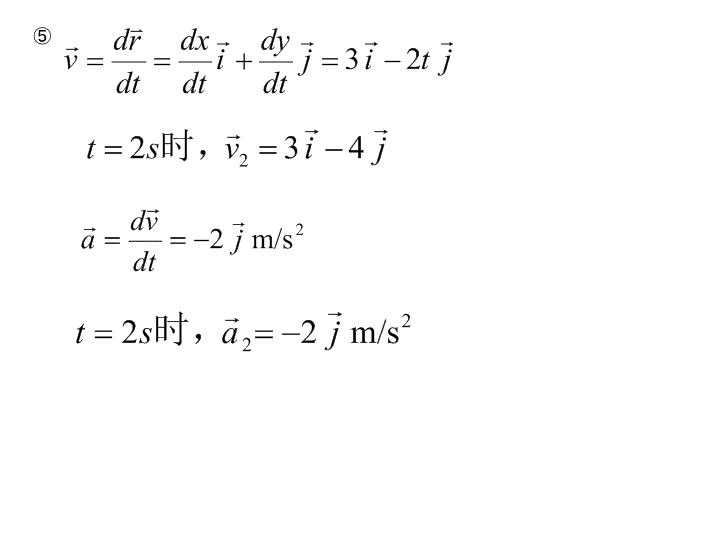《大学物理作业》PPT课件 129页

第一章作业\n指导：P7例1-1．一质点坐平面曲线运动，已知其运动方程为(m)。求：①质点运动的轨迹方程；②3s时的位置矢量；③第2内的位移和平均速度；⑤2s时的速度和加速度；解：①消去时间t得轨迹方程:②③\n⑤\nP18：1一质点在平面内运动，其运动方程为(SI)(1)写出质点位置矢量的表达式；(2)轨迹方程；(3)在时刻的位置矢量；计算在1～2s这段时间内质点的位移、平均速度(4)t时刻的速度表达式；(5)计算在1～2s这段时间内质点的平均加速度；在1s,2s瞬时加速度。解：（2）（1）消去时间t得轨迹方程:（3）\n（4）（5）\nP18：5，初速度为5．质点沿x轴运动，已知其加速度为，式中为大于零的常数。在时刻质点的坐标为，求质点的速度公式及运动方程。解：\nP18：6质点作半径为R的圆周运动，其经过的路程s和时间t的关系为其中b和c是大于零的常数，从t=0开始到切向加速度和法向加速度大小相等时所经历的时间。解：\nP18:7(1)(3)m的圆周作逆时针方向的圆周运动，在时刻质点的角速度及角加速度；(3)在一质点沿半径为时刻质点处在点，如图1-11所示，质点在0～这段时间内所经过的路程为(SI)求：(1)在s时刻的加速度。解：（1）（3）\nP21：2一汽车在半径R=400m的圆弧弯道上减速行驶。设在某时刻，汽车的速率为v=10m/s，切向加速度的大小为at=0.2m/s2。求汽车的法向加速度和总加速度的大小和方向？解：\n教材：P22:1-5质点在xy平面上运动，运动方程为（式中x,y以m计，t以s计）。（1）以时间t为变量，写出质点的位置矢量表达式；（2）描画质点的运动轨道；（3）求t=1s和t=2s时的位置矢量，计算只一秒内质点的位移；（4）求t=4s时质点的速度和加速度。解：（1）（2）抛物线一部分（如图示）（3）\n（3）\n教材：P22:1-7质点沿直线运动，加速度如果t=3s时，x=9m，v=2m/s2,求质点的运动方程。解：将t=3s时，x=9m，v=2m/s2代入得：\n教材P23：1-13一质点作半径为10m的圆周运动，其角加速度β=πrad/s2，若质点由静止开始运动，求质点第一秒末的（1）角速度，（2）法向加速度和切向加速度，（3）总加速度的大小和方向解：（1）（2）（3）与切线方向夹角：\n教材：P23：1-14一质点沿半径为0.1m的圆周运动，其角坐标可用下式表示：试问（1）在t=2s时，法向加速度和切向加速度各是多少？（2）当θ等于多少时，其总加速度与半径成45度角？解：（1）t=2s：（2）\n选择题：P16：11．下列说法正确的是：A）加速度恒定不变时，质点的运动方向也不变；B）平均速率等于平均速度的大小；C）当质点的速度为零时，其加速度必为零；D）质点作曲线运动时,质点速度大小的变化是因为有切向加速度，速度方向的变化是因为有法向加速度。一般情况：同A（D）\nP16：2质点作曲线运动，某时刻的位置矢量为，速度则瞬时速率是__，切向加速度的大小_，总加速度大小_。A）B）C）D）E）F）BFEP17：4一质点从静止出发绕半径R的圆周作匀变速圆周运动，角加速度为β，当该质点走完一周回到出发点，所经历的时间为：A）；B）；C）；D）条件不够不能确定。\nP17：6已知质点的运动方程为则它的加速度的大小和方向分别为：A）B）C）D）AP17：7一质点在平面上作曲线运动，设t时刻的瞬时速度为瞬时速率为V，0～t这段时间内的平均速度为，平均速率为它们之间有如下的关系：A）B）C）D）C\nP19:11．一质点作定向直线运动，下列说法正确的是：A）质点位置矢量的方向一定恒定，位移方向一定恒定；B）质点位置矢量的方向不一定恒定，位移方向一定恒定；C）质点位置矢量的方向一定恒定，位移方向不一定恒定；D）质点位置矢量的方向不一定恒定，位移方向不一定恒定。BP19:22．质点沿轨道AB作曲线运动，速率逐渐减小，如图所示，问哪一个图表示了在C处的加速度？c\nP19:44．已知半径为R＝1ｍ的圆作圆周运动，其角位置则在ｔ＝2ｓ时它的速度的大小为A）20m/sB）18m/sC）9m/sD）12m/sB填空题：P17:11．质点以初速度4米/秒沿x方向作直线运动，其加速度和时间的关系为a=3+4t，则t=3秒时的速度大小为____。\nP17:55．一质点在平面内运动,其，；、为大于零的常数，则该质点作。匀加速圆周运动P17：66．一质点在水平面上作匀速率曲线运动，其轨迹如图1-10所示，则该质点在点的加速度值最大，在该点的切向加速度的值为。B0\nP17：77．质点沿轴作直线运动，其运动方程为(SI)，则质点在时刻的速度=，。加速度为零时，该质点的速度\n第二章作业\n教材：P632-1MgNR’mgRxy如图中，质量为M的斜面装置，可在水平面上作无摩擦的滑动，斜面倾角为α，斜面上放一质量为m的木块，也可作无摩擦的滑动。先要保证木块m相对与斜面静止不动，为对M需作用的水平力F0有多大？此时m与M间的正压力为多大？M与水平面间的正压力为多大？解：对M：对m：\n\n指导：P4511．将质量为的小球挂在倾角的光滑斜面上，沿如图所示方向运动时，求绳中的张力及小球斜面的正压力。(2)当斜面的加速度至少多大时，小球对斜面的正压力为零？如图2-22所示，(1)当斜面以加速度解：压力为0时\n教材：P43例2-10θdθdsmgFT一个质量为m的小球系在细线的一端，线的另一端固定在天花板上的钉子上，线长为L，先拉动小球使线保持水平静止，然后松手使小球下落。求细线从水平位置摆下θ角时小球的速率。（用动能定理求解）解：\n教材：P652-8质量为1.5Kg的物体被竖直上抛，初速度为60m/s，物体受到的空气阻力数值与其速率成正比，即求物体升达最高点所需的时间及上升的最大高度。解：设竖直向上为y轴正向，物体受力代入初始条件t=0时，v=v0:当物体达到最高点时，v=0,所需时间：\n两边积分得：代入初始条件，t=0时，y=0:代入t=0.68得：\n解法二：\n教材：P662-18小球在外力的作用下，由静止开始从A点出发作匀加速运动，到达B点时撤销外力，小球无摩擦地冲上竖直的半径为R的半圆环，到达最高点C时，恰能维持在圆环上作圆周运动，并以次为速度抛出刚好落到原来的出发点A处。试求小球在AB段运动的加速度。解：因为小球到C点处恰能维持在圆环上作圆周运动，所以轨道对小球作用力为0，小球只受重力作用。B，C两点处机械能守恒，取B处为重力势能零点。从C到A的时间从A到B过程\n指导：P45：5劲度系数为的弹簧，一端固定在A点，另一端连一质量为的物体，靠在光滑的半径为的圆柱体表面上，弹簧原长为AB，作用下，物体极缓慢地沿所作的功。如图2-24所示。在变力表面从位置B移至C，求力解：V=0\n指导：P45：9解：设竖直向上为y轴正向，水面处为原点O一人从10米深的井中把10千克的水提上来，由于水桶漏水，每升高1米要漏去0.2千克水。问要把水匀速地从水面提到井口，人作功多少?\n指导：P49：4如图2-32所示，质量为的物体以从点沿斜面下滑，它与。到达点后压缩弹簧，压缩了后又被弹出。试求：弹簧的倔强系数；物体最后又沿斜面弹回多远？（设A、B间的距离为S，θ）斜面间的滑动摩擦系数为xsx0mgfN解：对m运用动能定理从A到B到弹簧被压缩到x0对于整个过程\n指导：P38例2-102-10．一质量为m=4kg的物体在力作用下由原点从静止开始运动，试求：①前2s内此力的冲量。②第2s末物体的速度。解：①由冲量的定义可得②由质点的动量定理得\n指导：P382-11例2-11如图2-11所示，质量分别为和两木块并排静止于光滑的水平面上，现有一子弹水平穿过两木块，所用时间分别为和，设每木块对子弹的阻力F相同，求子弹穿过后两木块的速度大小。解：子弹没进入木块B前，两木块以相同速度共同前进。设刚离开木块A时的速度为，取两木块为系统，有动量定理得：子弹进入B后，两木块分离，设木块B速度单独取木块B为系统，应用动量定理\nP45:66．质量10千克的物体静止于坐标原点，受到x方向力F的作用开始运动，问①在力(N)作用下运动3秒，其速度和加速度各为多少?(N)作用下移动3米，其速度和加速度各为多少？②在力解:(1)(2)\nP45:8一力作用于质量为（1）在开始（2）如果物体的初速度是，若物体受到的冲量后，物体速度达多少？的物体上。求：内，此力的冲量是多少？解:(1)(2)\nP48:22．如图2-31所示，光滑的水平面上，物体与劲度系数为k的轻质相靠系统静止。现突然放手，弹簧推动两物体运动，到达某位置时，、分离，求：①两物体分离时的速度②分开后，向前运动的最大距离。弹簧相连，物体而压缩弹簧，压缩量为b，整个解:(1)两物体在弹簧原长时分离（之后，m1将减速，m2将加速）（2）分开后系统机械能守恒\nP49:1010．一小船质量为100kg，船头到船尾共3.6m。现有一质量为50kg的人从船尾走到船头时，船头将移动多少距离？（设船和水之间的摩擦可忽略不计）解:船和人作为一系统，水平方向动量守恒以人的运动方向为正：代入上式：\n第三章作业\n教材：P1023-3m1MT2T1m1gRm2m2gN2NMg如图所示，两物体的质量分别为m1,m2滑轮的转动惯量为J，半径为r。（1）如m2与桌面间的摩擦系数为μ，求系统的加速度及绳中的张力（绳与滑轮间无相对滑动）（2）如m2与桌面间为光滑接触，求系统的加速度及绳中的张力。解：对m1对m2对滑轮\n（2）将代入上式得:\n教材：P102:3-6mMmRTmgMgN如图所示，质量为m的物体与绕在定滑轮上的轻绳相连，定滑轮质量M=2m，半径R，转轴光滑，设t=0时，v=0，求（1）下落速度v与t的关系。（2）t=4s时，m下落的距离。（3）绳中的张力。解：（１）（２）（３）\n教材：P102:3-7如图所示，有一飞轮，其转轴成水平方向，轴的半径为ｒ＝２ｃｍ，其上饶有一根细长的绳，在自由端先系以质量ｍ１＝２０ｇ的轻物，此物能匀速下降，然后改系一质量ｍ２＝５Ｋｇ的重物，则此物从静止开始，经过１０ｓ下降了４００ｃｍ。若略去绳的质量和空气的阻力，并设ｇ＝９．８ｍ／ｓ２．（１）求飞轮主轴与轴承之间的摩擦阻力矩的大小，（２）飞轮转动惯量的大小，（３）绳上张力的大小。mTmgrx解（1）挂m1时（2）挂m2时\n（3）\n指导：P66:1有一个长为L的均匀细杆，质量为m。求绕通过距其一端L/4处、并与杆相垂直的定轴的转动惯量。解：由于过质心的转动惯量为：由平行轴定理得：\n指导：P66:33.如图所示，一根细绳绕过两个定滑轮A和B，在绳的两端分别系两个物体m1=3kg和m2=1kg。若定滑轮A的质量MA=2kg，RA=0.2m；定滑轮B的质量MB=1kg，RB=0.1m。求两个滑轮之间绳中的张力和物体的加速度大小。m1gT1T1‘m2gT2T2‘T3T3’解\n教材：P1053-14om1m2A质量为m1=1.0Kg的匀质细棒，置于水平桌面上，榜与桌面间的滑动摩擦μ=0.2.棒一端O通过一垂直桌面的固定光滑轴。有一质量为m2=20g的滑块沿桌面垂直撞上棒的自由端A，碰撞时间极短，碰撞前后m2的速度分别为，且，求棒从开始运动到停下来所需的时间解：取滑块和棒为一系统，碰撞前后系统对O点的角动量守恒，取垂直纸面向外为正向。有棒运动时对O点的摩擦力矩为棒开始运动到停止所用的时间为t，由角动量定理得：代入数据得：t=0.122s\n教材：P105:3-15如图所示，刚体由长为l，质量为m的匀质细杆和一质量为m的小球牢固连接在杆的一端而成，可绕杆的一端O点的水平轴转动。先将杆拉至水平然后让其自由转下。若轴处摩擦可忽略，求（1）刚体绕O轴的转动惯量。（2）当杆与竖直线成θ角时，刚体的角速度。θ解：当杆在水平位置时，系统动能为零，杆摆到θ角位置时重力矩对系统做功为由功能原理得：\n教材：P105:3-16一长为l=0.4m的均匀木棒，质量M=1Kg，可绕水平轴O在竖直平面内转动，开始时棒自然地竖直悬垂。今有质量m=8g的子弹以v=200m/s的速率从A点射入棒中，假定A点与O点的距离为3l/4，求：（1）棒开始运动时的角速度，（2）棒的最大偏转角度。解：（1）以子弹、木棒为系统，因为，角动量守恒，即：\n（2）以子弹、木棒、地球为系统，木棒达最大偏角时，系统动能为零，重力势能增加了由机械能守恒：\n指导：P6622.如图所示，一根长为a、质量为m的均匀细杆可绕通过其一端的光滑水平轴o转动，另一端接有一质量为m的质点。现让该杆和质点系统从水平位置由静止开始自由下落，试用刚体定轴转动的理论求任意位置θ处杆和质点系统的角速度和角动量。解：解法二θ\n指导：P6777.一长为L的均匀直棒可绕其一端与棒垂直的水平光滑固定转动。抬起另一端使向上与水平面成600，然后无初速地将棒释放。己知棒对轴的转动惯量为1/3mL2，其中m和L分别为棒的质量和长度。求：（1）放手时棒的角加速度；（2）棒转到水平位置时的角加速度。600解：（1）（2）\n指导：P67:1010.一质量为M1长为L的均匀直杆，可绕通过其中心O且与杆垂直的光滑水平固定轴在竖直平面内转动。当杆停止于竖直位置时，质量为M的子弹沿水平方向射入杆的下端且留在杆内，并使杆摆动，若摆动的最大角为θ0，试求：（1）子弹入射前的速率V0，（2）在最大偏角θ时，杆摆动的角加速度。O解：（1）碰撞时角动量守恒上升过程，杆、子弹和地球系统机械能守恒\n（2）\n第六章电荷与电场\n小结1.真空中两个静止点电荷的库仑定律2.电场两个点电荷之间通过交换场量子而发生相互作用。场具有质量、能量和动量等。电磁场的场量子是光子。3.电场强度方向：与+q0受力方向相同。是矢量，单位：NC-1或Vm-14.电场强度的计算a.点电荷的电场b.点电荷系电场c.连续带电体电场d.电场分布具有对称性的带电体通常适用于无限长均匀带电直线、无限大均匀带电薄板、均匀带电球面和均匀带电球体。\n例6-6、求均匀带电球体(q、R)的电场分布。R解：对称性分析作以O为中心,r为半径的球形面S，S面上各点彼此等价，大小相等，方向沿径向。以S为高斯面：由高斯定理：令—体电荷密度\n例6-7、计算带电球层(R1,R2,)的电场分布。解：选一半径为r的球形高斯面SSr由高斯定理\n例6-8、求无限长均匀带电直线()的电场。解：对称性分析：P点处合场强垂直于带电直线,与P地位等价的点的集合为以带电直线为轴的圆柱面。高斯面：取长L的圆柱面，加上底、下底构成高斯面S。=0=0由高斯定理\n例6-9、求无限大均匀带电平面的电场(电荷面密度)。解：方向垂直于带电平面，离带电平面距离相等的场点彼此等价。选择圆柱体表面为高斯面，如图：σS=0根据高斯定理得——均匀电场，其方向由σ的符号决定。对称性分析：\n电势的计算(两种方法)1.场强积分法(由定义求)(1)首先确定分布;(2)选零势点和便于计算的积分路径;常选无穷远或地球电势为零。(3)由电势定义计算例6-10.求点电荷q场中的电势分布。解：令沿径向积分\n例6-11.求均匀带电球面电场中任一点处的电势。设球面半径为R，总带电量为q。解：已知其场强分布为选取无限远处为电势零点，在球壳外任一点P距球心O为r在球壳内任一点Q距球心O为r\n2.叠加法(一)—利用均匀带电球面的电势例6-12.求如图所示的结构电场中任一点的电势。已知大、小球面带电分别为q1、q2，半径分别为R1、R2解：带电球面的电势分布为r>R1R2>r1)，当大环以变角速度ω绕垂直于环面的中心轴旋转时，求小环中的感应电流及其方向。解：w(t)r1r2Oλ顺时针逆时针\n例8-9.某空间区域存在垂直向里且随时间变化的非均匀磁场B=kxcost。其中有一弯成角的金属框COD，OD与x轴重合。一导体棒沿x方向以速度v匀速运动。设t=0时x=0，求框内的感应电动势。vCODxBy解：设某时刻导体棒位于l处l任取xdxdS根据法拉第电磁感应定律：\n例8-11.长为l的螺线管，横断面为S，线圈总匝数为N，管中磁介质的磁导率为。求自感系数。解：线圈体积：\n例8-12.一电缆由两个“无限长”的同轴圆桶状导体组成，其间充满磁导率为的磁介质，电流I从内桶流进，外桶流出。设内、外桶半径分别为R1和R2，求：单位长度的一段导线的自感系数。解：两圆柱面间磁场为rdr\n例8-13.设在一长为1m、横断面积S=10cm2、密绕N1=1000匝线圈的长直螺线管中部，再绕N2=20匝的线圈。(1)计算互感系数；(2)若回路1中电流的变化率为10As-1，求回路2中引起的互感电动势；(3)M和L的关系。解：(1)设回路1通有电流I，磁场为：通过回路2的全磁通为：(2)(3)\n教材P3492如图所示，铜棒AB长为L，处在方向垂直纸面向内的匀强磁场B中，沿逆时针方向绕O轴作匀速运动，角速度为ω，求A，B两点的电势差。解：·aABLdllO\n教材P3493如图所示，一长直导线，通有电流I=5.0A，在与其相距d=5.0cm处放有一矩形线圈，共1000匝，线圈以速度v=3.0cm/s，沿垂直于长导线的方向向右运动时，线圈中的动生电动势多大？设线圈长l=4.0cm，宽a=2.0cm。解：\n教材P3494若上题的线圈不动，而长直导线通以交变电流(A)。线圈中的感生电动势是多少。I解：建立坐标系Ox，如图,x处的磁感应强度为：xO如图，取dS=ldxxdx根据法拉第电磁感应定律得根据楞次定律可知\n教材P3495在两平行导线所在的平面内，有一矩形导线框如图所示，如导线中电流随时间变化（即），试计算线圈中的感生电动势。解：\n教材P3495在两平行导线所在的平面内，有一矩形导线框如图所示，如导线中电流随时间变化（即），试计算线圈中的感生电动势。解：\n教材P3495在两平行导线所在的平面内，有一矩形导线框如图所示，如导线中电流随时间变化（即），试计算线圈中的感生电动势。解：