《大学物理波动》PPT课件 59页

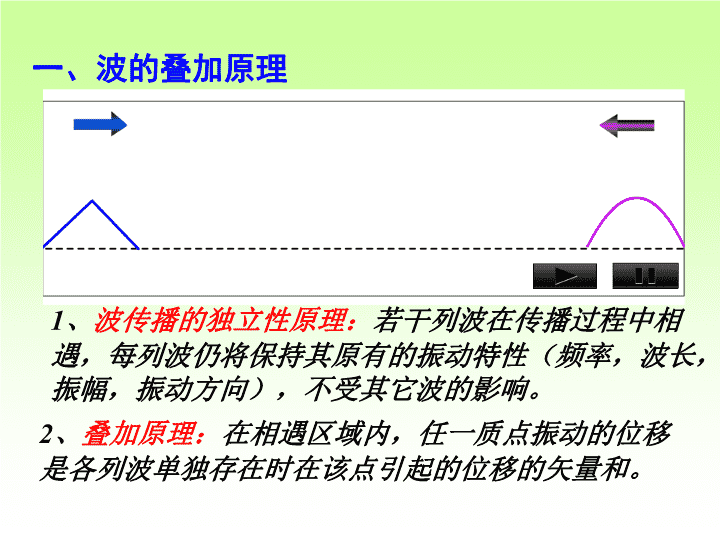
11－8波的叠加波的干涉驻波\n一、波的叠加原理1、波传播的独立性原理：若干列波在传播过程中相遇，每列波仍将保持其原有的振动特性（频率，波长，振幅，振动方向），不受其它波的影响。2、叠加原理：在相遇区域内，任一质点振动的位移是各列波单独存在时在该点引起的位移的矢量和。\n波源振动方程：S1S2PP点的相位差：二、同(振动)方向同频率的两列平面谐波的叠加\n振幅：初相：加强减弱\n三、波的干涉干涉：两列波在空间相遇（叠加），以至在空间的某些地方振动始终加强，而在空间的另一些地方振动始终减弱或完全消失的现象。干涉条件：1、两列波的频率相同2、振动方向相同3、有恒定的位相差相干波：能产生干涉现象的波S1S2\n相位差（1）当干涉相长（2）当干涉相消1）、合振幅加强和减弱的讨论（3）当相长相消\n讨论相长相消从能量上看，当两相干波发生干涉时，在两波交叠的区域，合成波在空间各处的强度并不等于两个分波强度之和，而是发生重新分布。这种新的强度分布是时间上稳定的、空间上强弱相间具有周期性的一种分布。2）、干涉后波的强度特征\n干涉现象的强度分布\n例题、如图AB为两相干波源，振幅均为5cm，频率为100Hz，波速为10m/s。A点为波峰时，B点恰为波谷，试确定两列波在P点干涉的结果。解：15mABP20m设A比B超前反位相P点静止\n例：相干波源位于同一媒质中的相距30m的A、B两点振幅相等，频率皆为100Hz,B超前A。波速为400m/s求AB连线上因干涉而静止的各点的位置。PAB30m解：设P为AB连线上一点分三种情况：\n（2）P在A左侧AB30mP结论：无论P在A左侧任何位置振动始终加强（1）P在B右侧AB30mP结论：无论P在B右侧何位置振动始终加强\nAB30mP（3）P在AB连线上x0建坐标系如图干涉静止干涉静止AB连线上因干涉而静止的各点是距A为\n1、形成条件：两列振幅相同的相干波沿相反方向传播叠加而成。四、驻波2、驻波方程驻波方程：Ox\n3、驻波波形的分析坐标：（2）波腹位置坐标：相邻两波节间距：（1）波节位置相邻波腹间距：1)、振幅分布\n波节波腹x驻波方程：相位两相邻波节之间的各点振动位相相同2)、相位分布\n结论：两相邻波节之间的各点振动位相相同，在一个波节的两侧（相邻两段）的各振动点反位相。相位x波节波腹0\n3)、能量分布波节：波腹：波节波腹x波节波腹0x最大位移平衡位置x波节波腹0波腹波节\n结论：在两波节之间波段进行动能势能的转化，能量在波节与波腹之间转移，在一个波长范围内无能量流出或流入x波节波腹04、弦线上的驻波\n弦上形成驻波的条件：（n=1,2,3,…)基频x波节波腹0\n\n讨论：LLL\n千斤码子如图二胡弦长，张力.密度频率波速基频谐频弦两端为固定点，是波节.\n波密媒质：密度与波速u的乘积u较大的媒质波疏媒质：密度与波速u的乘积u较小的媒质实验表明：当波从波疏媒质垂直入射到波密媒质时，反射点为波节；反之，波由波密媒质垂直入射到波疏媒质时，则反射点处形成波腹。四、入射波与反射波1、半波损失对于弦线上的驻波,如果反射端固定，则反射点为波节，如果反射端开放，则反射点为波腹。有半波损失无半波损失\n波疏媒质波密媒质：半波损失条件：反射点为波腹（无半波损失）反射点为波节（有半波损失）波疏媒质波密媒质：当波从波疏媒质垂直入射到波密媒质时对于弦波：当反射点固定时，有半波损失当反射点为自由，无半波损失当波从波疏介质传播到波密介质，分界面反射点是波节，表明入射波在反射点反射时有的位相突变相当于在波程上突变。这一现象称为半波损失。\n波密介质较大波疏介质较小当波从波疏介质垂直入射到波密介质，被反射到波疏介质时形成波腹.入射波与反射波在此处的相位相反，即反射波在分界处产生相位的突变.\n当波从波密介质垂直入射到波疏介质，被反射到波密介质时形成波腹.入射波与反射波在此处的相位相同，即反射波在分界处不产生相位突变.\n入射波方程：Ⅱ无半波损失反射波方程：有半波损失反射波方程：xyxⅠL波疏媒质波密媒质Ⅱ2、反射波ⅠⅠxLyx波疏媒质波密媒质O\n例题、已知驻波方程：求：（1）波速。（2）节点间的距离。（3）t=2.010-3秒时，位于x=5.0m处质点的速度。解：（1）标准方程：（2）节点间的距离（3）\n例题、平面简谐波振幅为A，以波速u入射到P点反射，以后形成驻波。设反射点存在半波损失，在o点t=0时，y=0，且向下运动。求驻波方程以及D点的振动方程。（DP=/6）解：oPxD入射波方程：反射波方程：\n反射波方程：入射波方程：oPxD驻波方程：\n驻波方程：D点的振动方程：（DP=/6）oPxD\n例题、有一简谐波，其表达式为：为了形成驻波，还应有一简谐波，并且在x=0处为一波节求其表达式解：设反向波因为x=0处为波节\n例设入射波的波动方程为在x=0处发生反射，反射点为一节点，求：（1）反射波的波动方程；（2）合成波（驻波）的波动方程；（3）指出各波腹和波节的位置坐标。解：（1）由题意，反射波方程为ⅡⅠⅠyx\n（2）驻波方程为ⅡⅠⅠyx\n（3）波节位置：所以即波腹位置：所以即ⅡⅠⅠyx\n驻波的应用辐射光源X射线驻波技术应用于金属原子纵深Z方向空间结构的探针，原子层所处的样品可以是凝固相的也可以是液相的，纵深空间探测范围可达100nm,分辩率可达0.1nm,灵敏度可达1012atom/cm2,并具有元素选择性。驻波管用于测量材料的声学特性，如材料的吸声系数、声阻抗等。在建筑声学设计中，设计师需要知道各种材料的声学特性，以便计算室内的混响时间；在汽车设计中，工程师用车内材料的声学特性计算车内降噪的效果。驻波管被广泛应用在新材料的研究中。\n发射频率接收频率人耳听到的声音的频率与声源的频率相同吗？讨论只有波源与观察者相对静止时才相等.§11-9多普勒效应\n波源的频率是波源在单位时间内振动的次数，或在单位时间内发出的“完整波”的个数接收器接收到的频率是接收器在单位时间内接收到的振动次数或完整波数波的频率是介质质元在单位时间内振动的次数，或通过介质中某点的“完整波”的个数\n因波源或观察者相对波传播的介质运动，致使观察者接收的波的频率发生变化的现象。一、多普勒效应二、多普勒效应的定量研究观察者OS波源u设波相对介质的传播速度为u(波速），波源的速度为周期频率分别为观察者速度：接收器接受到的频率为\n1波源与观察者均相对媒质静止t时刻的波前t+1秒时刻的波前u观察者接收的频率就是波源振动的频率\n2波源不动，观察者相对介质以速度运动\n接收频率提高！A）观察者朝向波源运动ut+1秒时刻的波前t时刻的波前\nB）观察者远离波源运动接收频率降低了！t+1秒时刻的波前ut时刻的波前\n3观察者不动，波源相对介质以速度运动\n波源运动时，波的频率不再等于波源的频率。这是由于当波源运动时，它所发出的相邻的两个同相振动状态是在不同地点发出的，这两个地点相隔的距离为VSTS，TS为波源的周期。yy\nA）波源朝向观察者以速度运动ut时刻的波前t+1秒时的波前接收频率增高了！yy\nt时刻的波前ut+1秒时刻的波前B）波源远离观察者以速度运动接收频率降低了！…….(4)yy\n4波源与观察者同时相对介质运动ut时刻的波前t+1秒时刻的波前接收频率增高了！…….(5)A）波源与接收者相互靠近\nB）波源与接收者相互远离ut时刻的波前t+1秒时刻的波前接收频率降低了！…….(6)\n公式归一：其中：波源静止观察者静止二者相互靠近二者相互远离取正值代入取负值代入。\n三、光波的多普勒效应特点：由光速不变原理，取决于波源与探测器之间的相对速度；由此可见，当光源远离接收器运动时，接收到的频率变小，因而波长变长，这种现象叫“红移”，即在可见光谱中移向红色一端。相反，则发生“紫移”。接近远离\n1）测量天体相对地球的视线速度远处星体发光有红移现象---宇宙大爆炸由红移可得恒星的退行速度四、多普勒效应的应用2）技术上，测量运动物体的视线速度如飞机接近雷达的速度、汽车的行驶速度、人造卫星的跟踪、流体的流速。\n警察用多普勒测速仪测速\n超声多普勒效应测血流速\n五冲击波（激波)当波源向接收器运动时，接收器接收的频率比波源的频率大，但当波源的速度等于波的速度，波源总在波阵面上。能量聚集区声障\n如果波源的速度等大于波的速度，波源总在波阵面前面。冲击波马赫角ut马赫数=飞机冲破声障时将发出巨大声响，造成燥声污染\n超音速的子弹在空气中形成的激波（马赫数为2）\n例、车上一警笛发射频率为1500Hz的声波,该车以20m/s的速度向某方向运动，某人以5m/s的速度跟踪其后，已知空气声速为330m/s。求该人听到的警笛发声频率以及在警笛后方空气中声波的波长。解：由已知条件得人听到的频率为：\n警笛后方的空气不随波前进，即有。空气中波长：解毕。