大学物理题集 14页

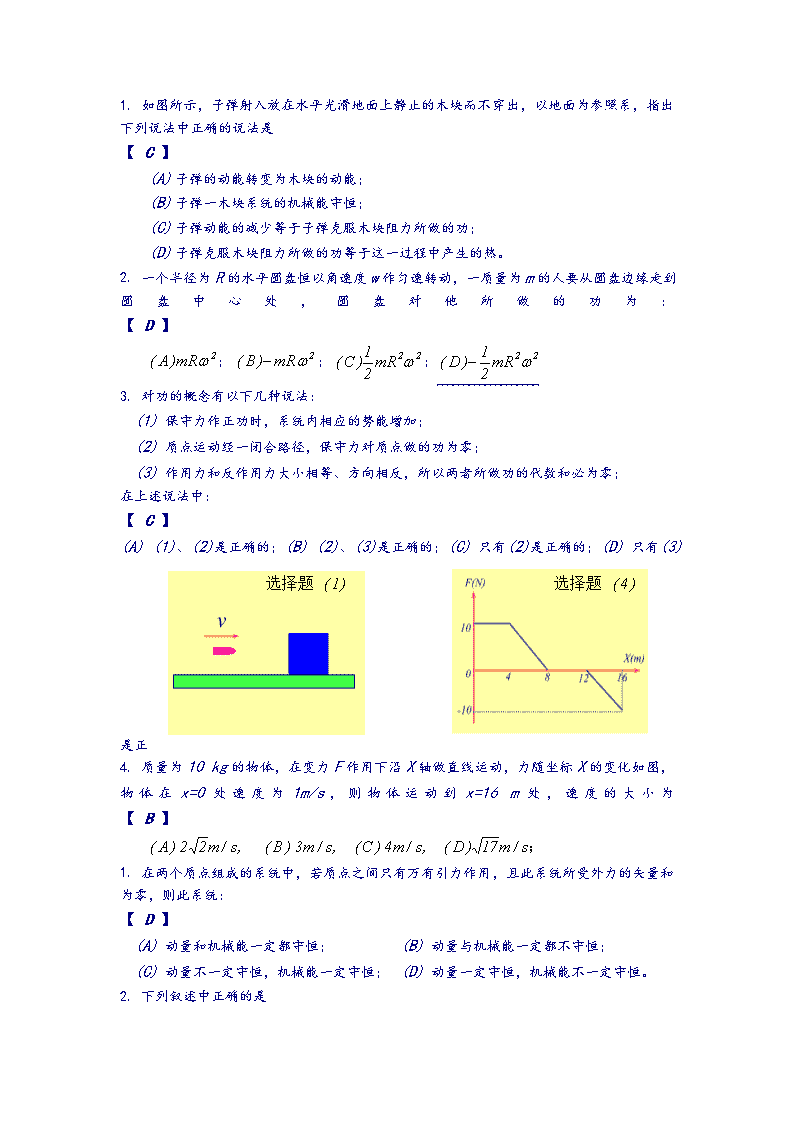
2.一物体在1秒内沿半径R=1m的圆周上从A点运动到B点，如图所示，则物体的平均速度是：【A】(A)大小为2m/s，方向由A指向B；(B)大小为2m/s，方向由B指向A；(C)大小为3.14m/s，方向为A点切线方向；(D)大小为3.14m/s，方向为B点切线方向。3.某质点的运动方程为x=3t-5t3+6(SI)，则该质点作【D】(A)匀加速直线运动，加速度沿X轴正方向；(B)匀加速直线运动，加速度沿X轴负方向;(C)变加速直线运动，加速度沿X轴正方向;(D)变加速直线运动，加速度沿X轴负方向4.一质点作直线运动，某时刻的瞬时速度v=2m/s，瞬时加速率a=2m/s2则一秒钟后质点的速度:【D】(A)等于零(B)等于-2m/s(C)等于2m/s(D)不能确定。1.一质点在平面上运动，已知质点的位置矢量为(a，b为常数)则质点作:【B】(A)匀速直线运动；(B)变速直线运动；(C)抛物线运动；(D)一般曲线运动。2.质点作曲线运动，表示位置矢量，S表示路程，at表示切向加速度，下列表达式中，【D】(1)；(2)；(3)；(4)。(A)只有(1)、(2)是对的；(B)只有(2)、（4）是对的；(C)只有(2)是对的；(D)只有(3)是对的。3.某人骑自行车以速率v向正西方向行驶，遇到由北向南刮的风(风速大小也为v)则他感到风是从【C】(A)东北方向吹来；(B)东南方向吹来；(C)西北方向吹来；(D)西南方向吹来。4.在相对地面静止的坐标系内，A、B两船都以的速率匀速行驶，A船沿X轴正向，B船沿y轴正向，今在A船上设置与静止坐标系方向相同的坐标系(x，y方向单位矢量表示)，那么从A船看B船它相对A船的速度(以为单位)为【B】\n1.如图所示，子弹射入放在水平光滑地面上静止的木块而不穿出，以地面为参照系，指出下列说法中正确的说法是【C】(A)子弹的动能转变为木块的动能；(B)子弹一木块系统的机械能守恒；(C)子弹动能的减少等于子弹克服木块阻力所做的功；(D)子弹克服木块阻力所做的功等于这一过程中产生的热。2.一个半径为R的水平圆盘恒以角速度w作匀速转动，一质量为m的人要从圆盘边缘走到圆盘中心处，圆盘对他所做的功为：【D】；；；3.对功的概念有以下几种说法:(1)保守力作正功时，系统内相应的势能增加；(2)质点运动经一闭合路径，保守力对质点做的功为零；(3)作用力和反作用力大小相等、方向相反，所以两者所做功的代数和必为零；在上述说法中:【C】(A)(1)、(2)是正确的；(B)(2)、(3)是正确的；(C)只有(2)是正确的；(D)只有(3)是正4.质量为10kg的物体，在变力F作用下沿X轴做直线运动，力随坐标X的变化如图，物体在x=0处速度为1m/s，则物体运动到x=16m处，速度的大小为【B】1.在两个质点组成的系统中，若质点之间只有万有引力作用，且此系统所受外力的矢量和为零，则此系统：【D】(A)动量和机械能一定都守恒；(B)动量与机械能一定都不守恒；(C)动量不一定守恒，机械能一定守恒；(D)动量一定守恒，机械能不一定守恒。2.下列叙述中正确的是\n【A】(A)物体的动量不变，动能也不变；(B)物体的动能不变，动量也不变；(C)物体的动量变化，动能也一定变化；(D)物体的动能变化，动量却不一定变化。3.在由两个物体组成的系统不受外力作用而发生非弹性碰撞的过程中，系统的【C】(A)动能和动量都守恒；(B)动能和动量都不守恒；(C)动能不守恒，动量守恒；(D)动能守恒，动量不守恒。4.一子弹以水平速度v0射入一静止于光滑水平面上的木块后，随木块一起运动，对于这一过程正确的分析是【B】(A)子弹、木块组成的系统机械能守恒；(B)子弹、木块组成的系统水平方向的动量守恒；(C)子弹所受的冲量等于木块所受的冲量；(D)子弹动能的减少等于木块动能的增加。5.质量为m的小球，以水平速度v与固定的竖直壁作弹性碰撞，设指向壁内的方向为正方向，则由于此碰撞，小球的动量变化为【D】(A)mv(B)0(C)2mv(D)-2mv1.一刚体以每分钟60转绕Z轴做匀速转动(w沿转轴正方向)。设某时刻刚体上点P的位置矢量为，单位，以为速度单位，则该时刻P点的速度为：【B】2.将一轻绳绕过一滑轮边缘，绳与滑轮之间无滑动，若(1)将重量为P的砝码挂在绳端;(2)用一恒力为F=P向下拉绳端，如图所示，分别用表示两种情况下滑轮的角加速度，则(1)两滑轮所受力矩方向是垂直纸面向里;滑轮转动方向为顺时针方向转动。(2)的关系是：【C】；；；1.花样滑冰运动员绕自身的竖直轴转动，开始时臂伸开，转动惯量为J0角速度为w0，然后她将两臂收回，使转动惯量减少为。这时她转动的角速度变为【C】\n2.如图所示，一质量为m的匀质细杆AB，A端靠在光滑的竖直墙壁上，B端置于粗糙水平地面而静止，杆身与竖直方向成q角，则A端对墙壁的压力大小为【B】(A)0.25×mg×cosq(B)0.5×mg×tgq(C)mg×sinq(D)不能唯一确定3.如图所示，一个小物体，置于一光滑的水平桌面上，一绳其一端连结此物体，另一端穿过桌面中心的孔，物体原以角速度w在距孔为R的圆周上转动，今将绳从小孔缓慢往下拉。则物体【D】(A)动能不变，动量改变;(B)动量不变，动能改变;(C)角动量不变，动量不变;(D)角动量不变，动量、动能都改变。1.对一个作简谐振动的物体，下面哪种说法是正确的？【C】(A)物体处在运动正方向的端点时，速度和加速度都达到最大值；(B)物体位于平衡位置且向负方向运动时，速度和加速度都为零；(C)物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D)物体处在负方向的端点时，速度最大，加速度为零。2.一沿X轴作简谐振动的弹簧振子，振幅为A，周期为T，振动方程用余弦函数表示，如果该振子的初相为，则t=0时，质点的位置在：【D】(A)过处，向负方向运动；(B)过处，向正方向运动；(C)过处，向负方向运动；(D)过处，向正方向运动。3.将单摆从平衡位置拉开，使摆线与竖直方向成一微小角度q，然后由静止释放任其振动，从放手开始计时，若用余弦函数表示运动方程，则该单摆的初相为：【B】(A)q；(B)0；(C)p/2；(D)-q5.一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的：\n【C】(A)竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动；(B)竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动；(C)两种情况都可作简谐振动；(D)两种情况都不能作简谐振动。6.一谐振子作振幅为A的谐振动，它的动能与势能相等时，它的相位和坐标分别为：【C】1.频率为100Hz ，传播速度为300m/s的平面简谐波 ，波线上两点振动的相位差为，则此两点相距：【C】(A)2m;(B)2.19m;(C)0.5m;(D)28.6m2 .一平面余弦波在时刻的波形曲线如图所示 ，则O点的振动初位相为：【D】3.一平面简谐波 ，其振幅为A ，频率为 ，波沿x轴正方向传播 ，设时刻波形如图所示 ，则x=0处质点振动方程为：【B】5.在简谐波传播过程中 ，沿传播方向相距为，（l为波长）的两点的振动速度必定：【A】(A)大小相同 ，而方向相反 ；(B)大小和方向均相同 ；(C)大小不同 ，方向相同；(D)大小不同 ，而方向相反 。\n8.一平面简谐波在弹性媒质中传播 ，在媒质质元从最大位移处回到平衡位置过程中：【C】(A)它的势能转换成动能；(B)它的动能转换成势能 ；(C)它从相邻的一段媒质质元获得能量 ，其能量逐渐增加；(D)它把自己的能量传给相邻的一段媒质质元 ，其能量逐渐减小 。9.一平面简谐波在弹性媒质中传播时 ，在传播方向上媒质中某质元在负的最大位移处 ，则它的能量是：【B】(A)动能为零 ，势能最大；(B)动能为零 ，势能为零；(C)动能最大 ，势能最大；(D)动能最大 ，势能为零 。1、分别以、S、和表示质点运动的位矢、路程、速度和加速度，下列表述中正确的是[B]A、；B、；C、a=；D、=v。1、质点在平面内运动时，位矢为(t)，若保持dv/dt=0，则质点的运动是[D](A)匀速直线运动；(B) 变速直线运动；(C) 圆周运动；(D) 匀速曲线运动。2、下列说法正确的是[D]A、质点作圆周运动时的加速度指向圆心；B、匀速圆周运动的加速度为恒量；C、只有法向加速度的运动一定是圆周运动；D、只有切向加速度的运动一定是直线运动。3、质点沿半径为Ｒ的圆周作匀速率运动，每转一圈需时间t，在3t时间间隔中，其平均速度大小与平均速率大小分别为[B](A) ,；(B) 0，；(C) 0，0；(D) ，0.4、质点作曲线运动，下列说法中正确的是[B]A、切向加速度必不为零；B、法向加速度必不为零（拐点除外）；C、由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零；D、如质点作匀速率运动，其总加速度必为零；E、如质点的加速度为恒矢量，它一定作匀变速率运动。1、质量为M的斜面静止于水平光滑面上，把一质量为m的木块轻轻放于斜面上，如果此后木块能静止于斜面上，则斜面将[B](木块能静止于斜面上说明两者运动速度相同.\n故动量守恒,两者水平速度必为零.)A、向右匀速运动；B、保持静止；C、向右加速运动；D、向左加速运动。2、某物体受水平方向的变力F的作用，由静止开始作无磨擦的直线运动，若力的大小F随时间t变化规律如图所示。则在0--8秒内，此力冲量的大小为[C]（A）0；（B）20N.S；（C）25N.S；（D）8N.S。(5x4/2+5x(6-4)+5x(8-6)/2=25)1、质点在恒力（N）作用下，从（m）运动到（m）处，则在此过程中该力做的功为[C]恒力是保守力,故做功与路径无关,取直线路径积分:A、67J；B、-67J；C、94J；D、17J。1、关于机械能守恒条件和动量守恒条件有以下几种说法，其中正确的是：[c]   A. 不受外力作用的系统，其动量和机械能必然同时守恒；(非保守内力做功未必为零)   B. 所受合外力为零，内力是保守力的系统，其机械能必然守恒；(外力做功未必为零)   C. 不受外力，而内力都是保守力的系统，其动量和机械能必然同时守恒；   D. 外力对一个系统做的功为零，则该系统的机械能和动量必然同时守恒。(合外力未必为零,非保守内力做功未必为零)3、对于一个物体系在下列条件中，哪种情况下，系统的机械能守恒[C]   (A)合外力为0，不存在非保守内力；(B)合外力不作功；(C)外力和非保守内力都不做功；(D)外力和保守内力都不做功。1、飞轮在电动机的带动下作加速转动，如电动机的功率一定，不计空气阻力,则下列说法正确的是[B]A、飞轮的角加速度是不变的；B、飞轮的角加速度随时间减少；[N=FV=Mω,ω↑,M↓,b↓]C、飞轮的角加速度与它转过的转数成正比；D、飞轮的动能与它转过的转数成正比。2、\n今有半径为R的匀质圆板、圆环和圆球各一个，前二个的质量都为m，绕通过圆心垂直于圆平面的轴转动；后一个的质量为m/2，绕任意一直径转动，设在相同的力矩作用下，获得的角加速度分别是β1、β2、β3，则有[D](J圆板=mR2/2J环=mR2J球=)A、β3＜β1＜β2B、β3＞β1＜β2C、β3＜β1＞β2D、β3＞β1＞β221、一自由悬挂的匀质细棒AB，可绕A端在竖直平面内自由转动，现给B端一初速v0，则棒在向上转动过程中仅就大小而言[B]力矩增大,角加速度大小不断增加(但为负值!).A、角速度不断减小，角加速度不断减少；B、角速度不断减小，角加速度不断增加；C、角速度不断减小，角加速度不变；D、所受力矩越来越大，角速度也越来越大。2、一长为，质量为m的匀质细棒，绕一端作匀速转动，其中心处的速率为v，则细棒的转动动能为[B]EK=Jw2/2=(1/2)(ml2/3)(2v/l)2=2mv2/3A、mv2/2B、2mv2/3C、mv2/6D、mv2/241、一质量为M，半径为R的飞轮绕中心轴以角速度ω作匀速转动，其边缘一质量为m的碎片突然飞出，则此时飞轮的[D][角动量守恒:Jω=(J-mR2)ω1+mR2ω1,ω1=ω;Ek=(J-mR2)ω2/2]A、角速度减小，角动量不变，转动动能减小；B、角速度增加，角动量增加，转动动能减小；C、角速度减小，角动量减小，转动动能不变；D、角速度不变，角动量减小，转动动能减小。2.对一个绕固定水平轴O匀速转动的圆转盘,沿图示的同一水平线射来两个方向相反,速率相等的子弹,并停留在盘中,则子弹射入后转盘的角速度[B].(Jω1+rmv–rmv=(J+2mr2)ω2↓)A.增大;B.减小;C.不变;D.无法确定\n1、两木块A、B的质量分别为m1和m2，用一个质量不计，倔强系数为k的弹簧连接起来，把弹簧压缩x0并用线扎住，放在光滑水平面上，A紧靠墙壁，如图所示，然后烧断扎线，正确的是[B]A.弹簧由初态恢复到原长的过程中，以A、B、弹簧为系统动量守恒。(有墙壁的外力作用)B.在上述过程中，系统机械能守恒。C.当A离开墙后，整个系统动量守恒，机械能不守恒。(机械能守恒)D.当A离开墙后，整个系统的总机械能为kx02/2，总动量为零。(总动量不为零)×2、在下列说法中：正确的结论[D]A.一个力的功，一对力（作用力与反作用力）的功，动能均与惯性参考系的选择无关。B.一个力的功，一对力的功，与参考系选择有关，而动能与参考系无关。C.动能、一对力的功与参考系有关，而一个力的功与参考系无关。D.一个力的功、动能与参考系有关，而一对力的功与参考系无关。(一对作用力与反作用力的功与参考系无关:F1×D(R+r1)+F2×D(R+r2)=F1×Dr1+F2×Dr2)3、质点系的内力可以改变[B]A、系统的总质量；B、系统的总动能C、系统的总动量；D、系统的总角动量。1、下列几个说法中哪一个是正确的？A、电场中某点场强的方向就是将点电荷放在该点所受电场力的方向；B、在以点电荷为中心的球面上，由该点电荷所产生的场强处处相同；C、场强方向可由定出，其中为试验电荷的电量，可正可负，为试验电荷所受的电场力；D、以上说法都不正确。[C]1、点电荷Q被曲面S所包围，从无穷远处引入另一点荷q至曲面外一点，如图所示，则引入前后：[D]（A）曲面S上的电通量不变，曲面上各点场强不变。（B）曲面S上的电通量变化，曲面上各点场强不变。\n（C）曲面S上的电通量变化，曲面上各点场强变化。（D）曲面S上的电通量不变，曲面上各点场强变化。2、关于高斯定理的理解有下面几种说法，其中正确的是[C](A)如果高斯面内无电荷，则高斯面上处处为零；(B)如果高斯面上处处不为零，则该面内必无电荷；(C)如果高斯面内有净电荷，则通过该面的电通量必不为零；(D)如果高斯面上处处为零，则该面内必无电荷。3、有两个点电荷电量都是+q，相距为2a。今以左边点电荷所在处为球心，以a为半径作球形高斯面，在球面上取两相等的小面积S1和S2，如图所示，设通过S1和S2的电通量分别为Φ1，Φ2，通过整个球面的电场强度通量为Φ3，则[D]A、Φ1＞Φ2,Φ3=q/ε0；B、Φ1＜Φ,Φ3=2q/ε0C、Φ1=Φ2,Φ3=q/ε0；D、Φ1＜Φ2,Φ3=q/ε0。1、在点电荷+q的电场中，若取图中p点处电势为零点，则M点的电势为[D](jM-jP=-=-,jM=-)A、B、C、D、2、半径为R的均匀带电圆环，其轴线上有两点，它们到环心距离分别为2R和R，以无限远处为电势零点，则两点的电势关系为(圆环电势:V=Q/(4pe0r)=Q/(4pe0r)\nA、B、C、D、[B]1、两个均匀带电的同心球面，半径分别为R1、R2(R1Eb>Ec；(B)EaUb>Uc；(D)UaF2)（A）向左平移；（B）向右平移；\n（C）向上平移（D）向下平移。2、一圆电流I,与它同心共面取一圆形回路L(如图所示),则磁感强度沿L的环流为[D](A)0，因为L上B处处为零；(B)，因为L上B处处与垂直；（C），因为L包围电流且绕向与dl流向相反；（D），但L上B处处不为零。3、对于安培环路定理的理解,正确的是[B]（A）若0,则必定L上B处处为零;（B）若0,则L包围的电流的代数和为零;（C）若0,则必定L不包围电流;（D）若0,则L上各点的B仅与L内电流有关。4、如图，匀强磁场中有一矩形通电线圈，它的平面与磁场平行，在磁场作用下，线圈发生转动，其方向是：[A]()(A)边转入纸内，边转出纸外；(B)边转出纸外，边转入纸内；(C)边转入纸内，边转出纸外；(D)边转出纸外，边转入纸内。4、一根很长的电缆线由两个同轴的圆柱面导体组成，若这两个圆柱面的半径分别为R1和R2（R1