(理学)大学物理 统计物理 46页

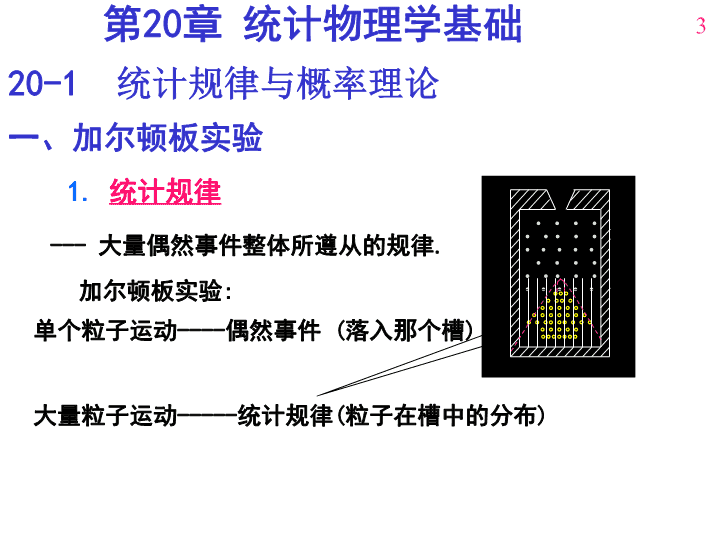
热是人类最早发现的一种自然力，是地球上一切生命的源泉。—恩格斯1\n宏观物体是由大量不停地运动的分子组成。用牛顿力学求解每个质点的运动，实际上不可能。热现象：与宏观物体的冷热状态相联系的自然现象研究热现象的性质和规律—热学实验模型普遍性和可信性热力学宏观理论热力学三大定律统计物理微观理论统计方法逻辑推理统计规律揭示本质，受模型局限知其然而不知其所以然涨落2\n1.统计规律---大量偶然事件整体所遵从的规律.加尔顿板实验:单个粒子运动----偶然事件(落入那个槽)大量粒子运动-----统计规律(粒子在槽中的分布)第20章统计物理学基础20-1统计规律与概率理论一、加尔顿板实验3\n单个粒子遵循牛顿定律;大量粒子遵从统计规律--牛顿运动定律无法说明2.统计规律特点:(2)是与单个粒子遵循的动力学规律有本质区别的新规律.(3)与系统所处宏观条件有关.(4)存在起伏(涨落).实验总观测次数为N,其中出现结果A的次数为NA事件A出现的概率(1)对大量偶然事件有效,对少量事件不适用。不矛盾3.概率的基本性质4\n(1)W=0为不可能事件;W=1为必然事件.(2)A,B为互斥事件,不可能同时出现,则出现A或B的总概率:---概率叠加原理归一化条件:对所有可能发生的事件的概率之和必定为1.或(3)J,K为相容事件(可同时出现），则同时发生J和K的概率.----概率乘法定理5\n热力学系统宏观量表征系统整体性质的物理量（如体积、压强)微观量广延量：有累加性(如质量、体积)宏观量是微观量的统计平均值外界热力学所研究的具体对象系统边界以外的部分，环境描写单个微观粒子运动状态的物理量（如分子速度、能量)强度量：无累加性(如温度、压强)孤立系统、闭合系统、开放系统20-2温度与压强6\n平衡态任何一个孤立系统，只要经过足够长的时间，必然将达到一个平衡态稳定态平衡态驰豫时间状态参量描述系统平衡态的宏观参量状态方程状态参量之间的函数关系一组态参量一个平衡态描述对应热力学参量：在不受外界影响的条件下，系统宏观性质不随时间改变的状态热动平衡7\n1)思路:压强由大量气体分子不断碰撞容器壁而产生；建立理想气体微观模型利用牛顿运动定律处理单个粒子的运动；利用统计规律处理大量粒子的行为；得到理想气体压强公式(1)气体分子看成质点；(2)除碰撞外,忽略其它力；(3)完全弹性碰撞；(4)分子的运动遵从经典力学规律压强为大量气体分子在单位时间内作用在器壁单位面积上的平均冲量。理想气体压强公式理想气体分子微观模型：8\n步骤1：速度为的某一个分子与ds碰撞一次后的动量变化为v'ivivi=2vixviv'idsxvidsxvixdt步骤2：求dt时间内,的所有分子施于ds的冲量。速度为步骤3：求dt时间内,各种速度分子对ds的总冲量。该分子施于ds的冲量为dt时间内,能与ds相撞的只能是位于底面积为ds,高为vixdt的斜柱体内的分子,该分子数为这些分子作用于ds冲量为：2)公式推导9\n步骤4：代入压强公式为分子的平均平动动能dt内各种速度分子对ds的总冲量为:其中n=N/V分子数密度步骤5：求统计平均值10\n3)推导中关于分子集体的统计性假设:①每个分子运动速率各不相同，而且通过碰撞不断发生变化；讨论:②平衡态时，每个分子的位置处在容器内空间任何一点的概率是一样的，或者说，分子按位置的分布是均匀的。③在平衡状态时，每个分子指向任何方向的概率都是一样的，或者说，分子速度按方向的分布是均匀的压强公式将宏观量p和微观量的统计平均值联系在一起。11\n2.气体分子平均平动动能与温度关系温度是气体分子平均平动动能的量度,具有统计意义。12\n例在容积V=4×10-3m3的容器中，装有压强p=5×102pa的理想气体，则容器中气体分子的平动动能总和为多少？解：13\n例下列各式中那一式表示气体分子的平均平动动能？解气体分子的平均平动动能为答案(A)14\n例:（1）在一个具有活塞的容器中盛有一定的气体。如果压缩气体并对它加热，使它的温度从270C升到1770C，体积减少一半，求气体压强变化多少？（2）这时气体分子的平均平动动能变化多少？解：15\n16\n例一容器中贮有理想气体，压强为0.010mmHg高。温度为270C，问在1cm3中有多少分子，这些分子动能之总和为多少？解：分子平均平动动能为故N个分子总动能：17\n一等概率假设处在平衡态的孤立体系,其可能的微观态出现的几率相等----平衡态统计理论的基础如果可能微观态总数为，则系统的任意微观态出现的概率均为1/:系统自发趋向于最概然分布求经典粒子（例：气体分子）按能量的最概然分布的思路:(1)求将N个粒子按的各种量子态中去的可能占据的方式数Ω分别放到能量为（2）求Ω取最大值的分布,即最概然分布(3)求在最概然分布下,每个能级上的粒子数20.3麦克斯韦气体分子速率分布律（预备知识）18\n能级上每个量子态被占据的概率讨论过程中要用到等概率假设和约束条件约束条件:孤立体系(1)求将N个粒子按的各种量子态中去的可能占据的方式数Ω分别放到能量为（2）求Ω取最大值的分布,即最概然分布(3)求在最概然分布下,每个能级上的粒子数19\n二.麦克斯韦--玻尔兹曼统计(M-B分布)经典粒子彼此可以区分,每个量子态中的粒子数不受限制.2个经典粒子在3个量子态中的可能分布（共9种)(M-B分布)哈尔滨飞机火车汽车飞机火车汽车北京上海共有种方案（2个不同粒子放入3个盒子，分2步完成。）2个不同色子扔下，先扔1个，再扔另1个，共62种状态20\n(2)个粒子分别占用能级的个量子态的占据方式为因而N个可区分粒子，分为个粒子的组合方式为(3)(1)Ni个经典粒子分布在能级的个量子态上的占据方式为21\n(2)为使Ω极大,令利用斯特令公式因而y123x22\n由宏观约束条件（3）由宏观约束条件确定由拉格朗日乘子法原理23\n最后可得由可得经典粒子按能级的最概然分布M-B分布理论和实验证明24\n20.4麦克斯韦气体分子速率分布律1.麦克斯韦分子速度分布律利用M-B分布可导出在没有势场情况下，理想气体按速度的分布规律。对理想气体，在温度T的平衡态下:分子速度在的概率25\n利用26\n2.麦克斯韦分子速率分布律如果不考虑分子速度的方向，只考虑速度大小,由并对由在T的平衡态下，理想气体分子速率在v--v+dv范围内的概率速率分布函数----概率密度麦克斯韦速率分布函数满足归-化条件:ovzvxvyv*扩大为27\n0vf(v)........。银蒸汽真空麦克斯韦速率分布实验银相对厚度28\nvv2vpv~v+dvf(vp)of(v)v1讨论:(1)f(v)曲线下面积的物理意义寛度为dv的窄条面积:曲线下总面积:V1-V2区间的面积:29\n（3）最概然速率（最可几速率）---f(v)-v曲线极大值所对应的速率vpvp的物理意义：vp附近概率密度最大（同样速率间隔dv,速率在vp--vp+dv的分子数最多)由及vv2v~v+dvof(v)v1（2）由同理，30\nvof(v)3三种速率平均速率方均根速率最概然速率vp可以看出前面说明是合理的31\n玻尔兹曼能量分布律等温气压公式外力场中,粒子在速度在的分子数对所有速度积分,由速度分布函数的归一化条件,得得体积元dxdydz内的总分子数:气体分子按能量的分布规律（玻尔兹曼能量分布律）32\n用空间粒子数密度表示:n0为Ep=0处的粒子数密度重力场中重力场中粒子按高度的分布--恒温气压公式33\n空气密度气体压强可以看作单位面积上空气柱重量由重力场中粒子按高度的分布另一种推导方法：34\n20.5能量均分定理理想气体的内能自由度:气体分子：单原子（看作质点）3个平动自由度双原子3个平动自由度(质心),2个转动自由度(联接方式)刚性5个自由度（无振动）非刚性6个自由度(1个振动自由度)确定一个物体的空间位置所需的独立坐标数oxyzC(x,y,z)多原子3个平动自由度,3个转动自由度，若干个振动自由度oxyzC(x,y,z)35\n能量均分定理:在温度为T的平衡态下,分子每一个可能的自由度都占有相同的能量kT/2.设分子有t个平动自由度,r个转动自由度,s个振动自由度,由于每个振动自由度又占有振动动能和振动势能2份能量,该分子的平均能量为:理想气体(刚性分子),S=0,则单原子双原子多原子(i=t+r+2s)常温下例：粒子的平均平动动能36\n理想气体内能:1mol理想气体分子数为NA,内能为:质量为m的理想气体内能为:分子的平均能量为:(i=t+r+2s)37\n分子热运动踫撞示意图20.7分子平均碰撞次数和平均自由程1.分子平均踫撞频率dddu分子平均踫撞频率38\n由于分子向各个方向运动的概率相同,所有两分子运动方向的平均夹角将是0°至180°之间的平均值90°因此所以即每秒内一个分子要发生几十亿次踫撞.分子平均踫撞频率常温常压下,数量级为例：H2常温常压39\n2.平均自由程平均自由程:分子在连续两次踫撞间所通过的自由路程的平均值将p=nkT代入上式得分子平均踫撞频率约为分子直径10-10米的1000倍40\n物理意义？速率大于V1的速率平均值由例141\nⅠⅡvf(v)温度T相同，哪个是H2?哪个是O2?都个是H2,温度不同，哪个温度高？Vp1Vp20例242\n用简化运算例343\n例4：求300K时，空气中速率在vp附近和10vp附近单位速率区间的分子数占总分子数的百分比各是多少？解：44\n例5已知：N个粒子的速率分布函数为（C为待定常数）{求：平均速率解：由45\n例6一瓶气体由N个分子组成。试证不论分子速率分布函数如何，总有证：46