大学物理课件 (9) 29页

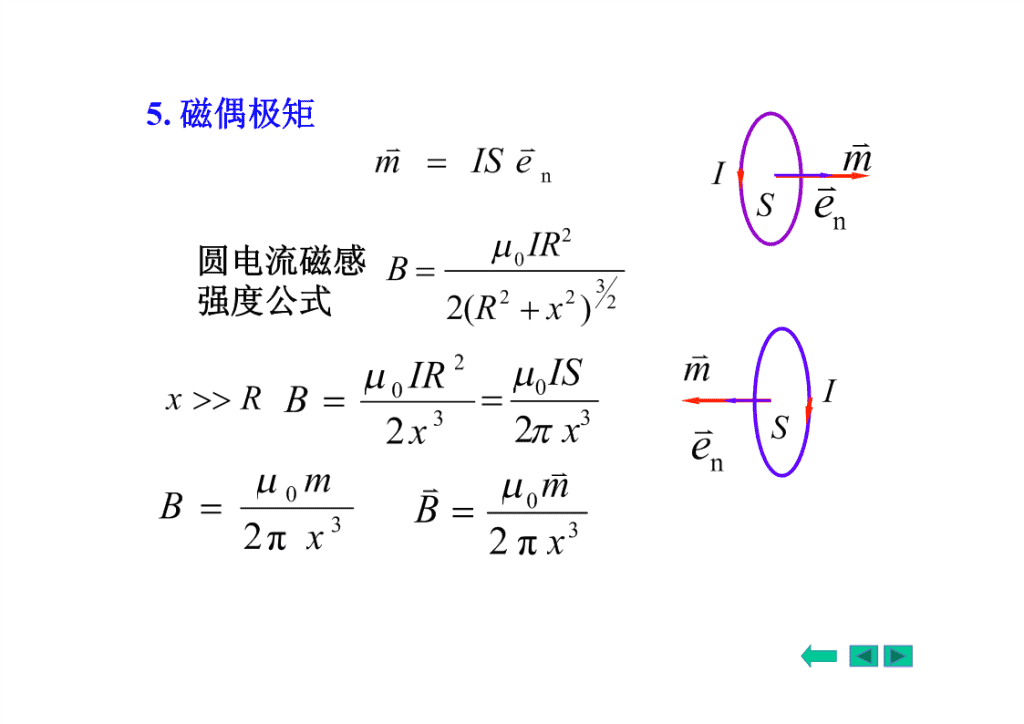
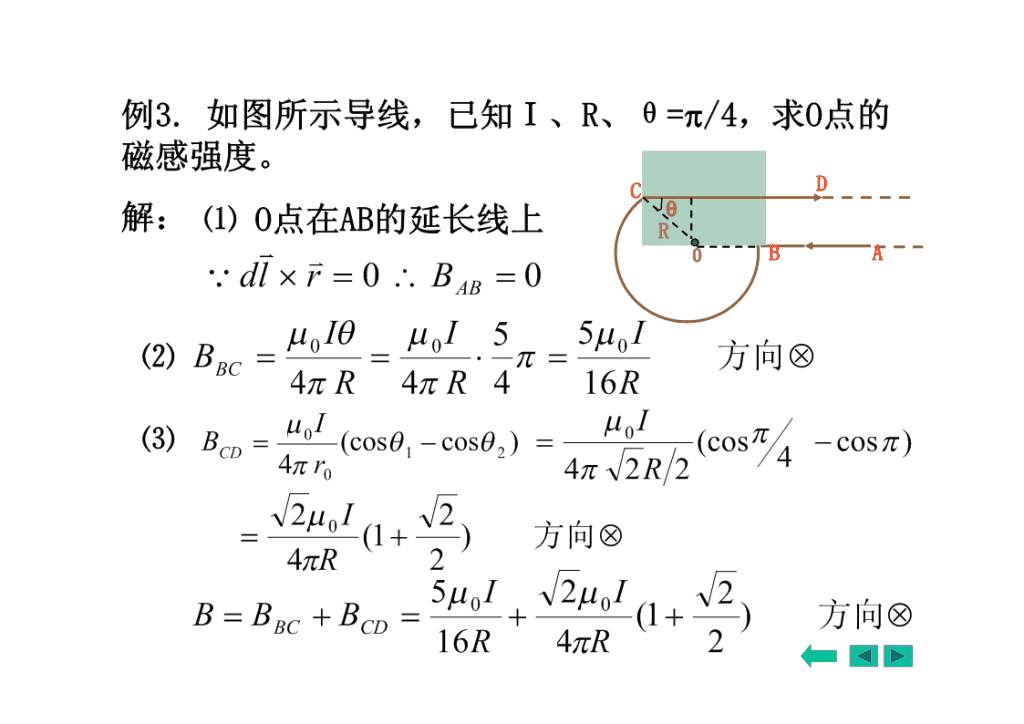
2zIR0BdB3z2(R2z2)2dBp•讨论：2N0IRzdB1.N匝线圈Br32222(Rz)0yRIIdl02.z0B(圆心处)2Rx2IRIS003.zRB332z2z4.一段圆弧导线圆心处的磁感强度IdlIdIdB00B024R4R4Rθ─圆弧所对圆心角，用弧度表示。\n5.磁偶极矩mISemnISen2IR圆电流磁感B03强度公式2(R2x2)22mxRB0IR0ISmI2x32x3Sen0mmBB0332πx2πx\n例3.如图所示导线，已知Ｉ、R、θ=/4，求O点的磁感强度。CDθ解：⑴O点在AB的延长线上R0BAdlr0B0ABII55I000⑵B方向BC4R4R416R0I0I⑶B(coscos)(coscos)CD1244r042R22I20(1)方向4R25I2I200BBB(1)方向BCCD16R4R2\n例4.如图所示导线，求0点的磁感强度。II0I0B0BB(圆心处)P2R4R4πr（1）（4）RI0B0xBI0IoB04πd02Rd（2）I×*oRB0I（5）×0RRo4RI12（3）I•*oIB0IIIR0B000×8R04R4R4πRo211\n例5.均匀密绕直螺线管轴线上的磁场。已知R、Ｉ、、、单位长度的匝数n。12解：由圆形电流磁场公式R12IR2B0Px223/2xdx（2xR）dInIdxl22RnIdxnIRdx00dBpBdB32232(R2x2)22(Rx)222222xRctgdxRcscdRxRcsc2nI00BnIsind(coscos)21122\nnI0BcoscosR21122Px讨论：l（1）P点位于管内轴线中点1π2l/2cos1cos2cos222l/2RnIl0BnIcos021/2222l/4R若lRBnI0\nRnI1B0coscos221Px2012l无限长螺线管轴线中部BnI0（2）半无限长螺线管轴线上端点π1,0或π,BnI12120222nIB010nI2Ox-L/2L/2\n例7.如图所示，电流I均匀流过宽为2d的无限长薄金属板，试求通过板的中线并与板面垂直的平面上一点的磁感强度。ydB解：把薄片分成许多宽为dxPIdB的无限长载流直导线dIdx2dIdII00dBdxdBy0ryr2r4drIyx0dxBBdBdBcosdx0xxx4drr222rysecdd2xytgdxysecdI0Iarctgdy0IdB0d0darctg4d04darctgd2dyy\nIarctgd0IdB0ydarctg4darctgdy2dyddBy讨论：⑴y<>d，arctyyydd—无限长载流直导线IdIB00Barctg2dy2yB\n三运动电荷的磁场j电流密度0IdlrIelSdBjnqvIjdS4r3SSdlIdljSdlnqSvdlnqSdlvr0jdB3nSdlndVdN4rSdB0qvr0qver+++Bv32+dN4r4r++qvsin大小：B04r2vv+-方向：正电荷vr的方向;rrB负电荷vr的反方向×B\n例8.设半径为R的带电圆盘的电荷面密度为，并以角速度绕通过盘心垂直盘面的轴转动，求盘心处磁感应强度和圆盘的磁矩。解一：dI2rdrR2O=rdrrdIdr0dB2rR10BdBdrR0202R1224mdmrdIrrdrR04\n解二：0qverB2R4rOdqvr0rdB34rdrdqv0dB24rdq2rdrvrdB0dr20R1BdBdrR0022方向垂直纸面向外\n§7-5磁通量磁场的高斯定理一磁感线1.规定：曲线上每一点的切线方向就是该点的磁感强度B的方向，曲线的疏密程度表示该点的磁感强度B的大小.III\nIISSNN2.磁感线的性质：⑴磁感线不会相交。⑵磁感线是围绕电流的闭合曲线。\n二磁通量磁场的高斯定理1.磁感线的密度规定：磁场中某点处垂直B矢量的单位面积上通过的磁感线数目等于该点B的数值.BSNBS2.磁通量（）n通过磁场中某一曲面的磁感线数。均匀磁场的磁通量：BBScosBS\nn非均匀磁场的磁通量：BdBcosdSBdSdSBcosdBdSSS3.闭合曲面的磁通量：BdS1BcosdBdSBSS1B1/2为正，S磁感应线穿出B2/2为负，2磁感应线穿入dS2则SBcosdSBdS0\n4.磁场的高斯定理：SBdS0通过任意闭合曲面的磁通量必等于零。5.稳恒磁场和静电场高斯定理的比较1nEdSqi—有源场电场线不闭合Soi1SBdS0—无源场磁感应线闭合6.单位：B的单位—特斯拉（Ｔ）2的单位—韦伯（Ｗｂ）1Wb1T1m\n例1.如图载流长直导线的电流为I,试求通过矩形面积的磁通量.解:先求B，对变磁场给出dΦ,后积分求ΦI0BB//SB2πxIdΦBdS0ldx2πxIxdxlΦBdS0Ild2dxd1Sdd2π1x2o0Ild2xΦln2πd1\n§7-6安培环路定理一安培环路定理的表述：在真空中，磁感应强度B矢量沿任何闭合曲线L的线积分，等于闭合曲线所包围电流的代数和的倍。onIBBdloIiLi1dl二安培环路定理的验证oR（1）圆形环路包围电流l0IIIBBdl0dl0dl2πRl2πR2πRlBdlI(回路l与I成右螺旋)0l\nIB若回路绕向为顺时针时，则Idl0Bdldl0IoRl2πRll（2）任意环路包围电流IoBdlcosrdI2rLBBdlBcosdldLLrII2dloorddIL0o2r2\n（3）电流在环路之外dlcosrdIBdBdlcosrdrdl´rdlIIooBB2r2rBdlBdlBdlcosBdlcosIIoordrd02r2r结论：Bdl0L\n（4）环路包围多根载流导线I4IIIBBBB32112nLBdlBBBdlLL12nBdlBdlBdlL1L2LnnoI1oI2oInoIii1\n三讨论：1.电流I为代数量当电流方向与积分路径的绕行方向构成右手螺旋关系时电流为正，反之为负。2.环流Bdl由闭合曲线所包围的电流决定，L与回路外的电流及回路大小形状无关。3.安培环路定理表达式中的磁感应强度B是闭合曲线内外所有电流产生的磁感应强度。4.稳恒磁场和静电场环路定理的比较BdloI—非保守场（有旋场）LLEdl0—保守场5.利用环路定理可求电流对称分布情况的磁感强度。\n*磁感应强度是轴矢量•镜像反射的变化规律–极矢量：与镜面平行分量不变，垂直分量反向•dl、r、v、F、E–轴矢量：与镜面垂直分量不变，平行分量反向–两个极矢量叉乘＝轴矢量•由毕奥－萨筏尔定律决定dlr–B是轴矢量推论：镜面对称的载流系统在镜面处产生的磁感应强度垂直于镜\n四安培环路定理的应用例1.载流长直螺线管内的磁场无穷远处•密绕，L>>R；磁场为0•B是轴矢量，垂直于镜面；•论证管外B=0–管外即使有磁场也是沿轴向的；–作回路如a，可以证明p点B=0;•求管内任意P点的磁场nIaBdlIBa0i0LS内BdlBdlBdlBdlBdlB0nILP长载流螺线管内部磁场处处相等,外部为零.\n例2.螺绕环内的磁感应强度。设电流为I，匝数为N。解：对称性分析，密绕的螺绕环内磁感线为同心圆，同I一圆环上B的大小相等，环····B··外B为零，取回路L。·r·L··BdloI···LdB2rNIoNINonBnIB2r2ro当2rd时，螺绕环内可视为均匀场.\n例3.无限长载流圆柱形导体的磁场分布。设半径R，电流I均匀分布在截面上。R解1）对称性分析2）选取回路rrLrRBdl0IlII02πrBIB02πr.dBI×πr2dI0rRBdlI0lπR2BB20r0Ir2πrBIB22R2πRRr\n讨论：无限长载流圆柱面的磁场L1rBIRLr2oRr解：0rR,Bdl0B0lIrR,0BdlIB0l2πr\n例4.无限大薄导体板均匀通过电流的磁场分布。dB1解1)对称性分析2）选取回路dBP设：电流密度为jdcdBBdlI2Looo2BLojLBjL2ab两侧为均匀磁场，与离板的距离无关讨论：两无限大平行载流平面，电流密度为j，求两平面之间和之外空间的磁感强度11Bjjj内00022•×××ו11Bjj0外0022