大学物理实验数据处 47页

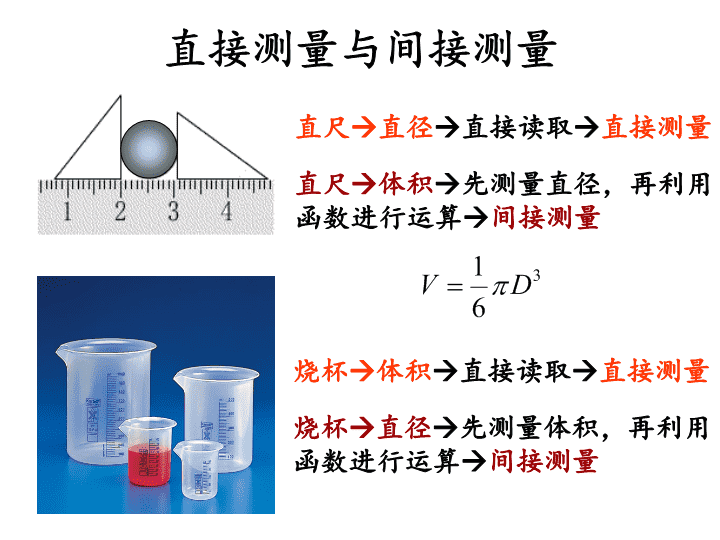
大学物理实验数据处理基础知识教师：高明向9/9/2021时间：2011.9.7，2011.9.8，18:30-21:30地点：5-401班级：航海1001-1007，物联网1001-1002\n一测量的概念测量就是以确定被测量对象的量值为目的的所有操作。同时记录测量结果的大小和单位，二者缺一不可。大学物理实验中,如果没另加说明,对一个物理量的多次测量，都必须在相同的实验条件下进行，这称为等精度测量。\n直接测量与间接测量直尺直径直接读取直接测量直尺体积先测量直径，再利用函数进行运算间接测量烧杯体积直接读取直接测量烧杯直径先测量体积，再利用函数进行运算间接测量\n测量值、平均值（最佳估计值）测量值：通过测量所获得的被测物理量的值。平均值（最佳<估计>值）：在相同条件下，对某物理量进行n次测量，这n个测量结果x1,x2,x3…xn,称为一个测量列，取这n次独立测量值的算术平均值，记为。即\n真值与测量误差真值：被测量物理量所具有的客观、真实的量值，用x0表示，它不能通过测量得到。在处理测量数据时常用物理量的平均值代替其真值(称为约定真值)。当测量次数趋于无穷，最佳值将无限接近真值。(绝对)误差：即测量值与真值之差，记为εε=xi-x0相对误差：用E表示，定义为绝对误差真值相对误差=×100%\n二测量不确定度的概念与计算每次所得的测量值总是在真值[最佳值]附近一定的范围内，当把范围扩大时，测量值出现在次范围内的几率大，反之则小。这种与一定的（测量值存在于真值[最佳值]附近的）几率相联系的、真值[最佳值]附近的一定范围，就是测量的不确定度,用u表示。相应的几率称为置信率，这个范围称为置信区间。例如：在对某物体长度测量的实验后得到，P=68%，表明该物体长度的测量值落在下列区间的几率为68%：\n扩展不确定度一般来说，被测量的测量值落在区间的概率大约只有68%，为了提高置信率，常将不确定度u乘以一个扩展因子m，即得扩展不确定度，用U表示。在物理实验课程中，扩展因子m=2，即此时置信率约为95%。\n正确理解不确定度不确定度可以根据实验、资料、经验等进行评定，从而可以定量确定。表示合理赋予的测量列的分散性。u越大，表示测量列的分散性越大.反之，越小。如：测量一物体的长度，得到两个测量列：3.01，3.02，3.00，2.99，2.98…(分散性小)3.05，2.95，2.98，3.00，3.10…(分散性大)与误差的区别。测量不确定度的大小可以定量确定，而误差是个确定的值，但是无法计算出来（因无法知道被测量的真值）。\n直接测量量的A类和B类不确定度按不确定度的数值评定方式，可分为两类：A类不确定度：用统计方法确定的量B类不确定度：用其他方法确定的量使用此式时,测量次数n应充分多,要求n≥6。1.根据经验确定。2.如果已知被测量的测量值xi分散区间的半宽为a，且落在区间的概率为100%，通过对其分布规律的估计可得出B类不确定度为：k是包含因子，取决于测量值的分布规律.\nB类不确定度的计算物理实验中没有特别说明时，使用矩形分布(平均分布)计算B类不确定度，此时。包含因子k的确定分散区间半宽度的确定1.如果检定证书、说明书等资料明确给出了不确定度U(x)及包含因子k时，则a=U(x)，B类不确定度为例题校准证书上给出标称值为1kg的砝码质量m=1000.00032g，包含因子k=3，不确定度为U=0.24mg，由此可确定砝码的B类不确定度\n2.在缺乏任何信息的情况下，一般使用均匀分布，，而a则取仪器的最大允许误差(误差限)△(x)，所以B类不确定度为例题知道某游标卡尺的仪器最大允许误差为Δ=0.05mm，使用矩形分布计算不确定度。B类不确定度的计算\n1仪器的示值误差限通常可以在仪器说明书或技术标准中查到，讲义中第13页列出了几种常用仪器的示值误差限，需要时可查阅。2电测量指示仪表的最大允许误差与仪表的准确度级别有关。电测量仪表的准确度级别分为七级：0.1，0.2,0.5，1.0，1.5，2.5，5.0。由仪表的准确度级别与所用量程可以推算出仪表的示值误差限：△=量程×准确度等级/100电学仪表的准确度等级通常都刻写在度盘上，使用时应记下其准确度等级，以便计算。仪器最大允许误差（误差限）的确定方法\n2.5级△=5×2.5/100=0.125V\n3.数字显示仪表在缺乏说明的情况下，取其最小分度值作为其仪器的示值误差限。△＝0.01mA\n4.未加说明的仪器，如果无法得知其误差限，一般取仪器最小分度的一半作为其仪器误差限。△=0.5mm\n直接测量量的合成不确定度A类和B类不确定度的合成不确定度uc(x)：说明：当进行的测量只有1次时，取则如果一个测量量的B类不确定度有多个部分构成，则B类不确定度的合成不确定度为\n例题用螺旋测微计测某一钢丝的直径，6次测量值分别为：0.249,0.250,0.247,0.251,0.253,0.250;单位mm，已知螺旋测微计的仪器误差为Δ仪=0.004mm，请给出测量的合成不确定度。解：测量最佳估计值A类标准不确定度B类标准不确定度合成不确定度\n间接测量量的不确定度间接测量量，其中为直接测量量Y的估计值y的不确定度，要由X1,X2,X3,…Xn的不确定度适当合成求得，称为估计值y的合成不确定度,记为uc(y)。\n间接测量量的不确定度计算（续）对于形如的函数形式（和差关系）,合成标准不确定度的计算方法为:【例题】某实验的测量式为Y=4X1+3X2，X1,X2为直接测量量，其中u(x1)=0.03g,u(x2)=0.05g,则间接测量量的合成不确定度为\n间接测量量的不确定度计算（续）对于形如的函数形式（积商关系），则先求其相对合成不确定度：说明：对于被测量Y的平均值，按如下方式计算：合成不确定度\n间接测量量的不确定度计算（续）【例题】圆柱体的体积公式为。设已经测得，，写出体积的相对合成不确定度表达式。解：此体积公式形如其中，，，。体积的相对合成不确定度表达式为根据\n三测量结果的表达物理实验中，用扩展不确定度报告测量结果单位单位下列形式是错误的：单位单位\n四物理实验中的有效数字及其运算规则仪器的读数规则首先读出能够从仪器上直接读出的准确数字，对余下部分再进行估计读数。即将读数过程分为直读和估读。01234567直读——准确数字7.4cm——可靠数字估读——余下部分约为0.03cm——存疑数字物体的长度即为7.43cm有效数字：物理实验中的有效数字是针对测量中的数据定义的概念,是一个有单位的数据,由若干位可靠数字及末尾一位存疑数字组成。7\n正确理解和使用有效数字1.实验中的数字与数学上的数字是不一样的。如数学的8.35=8.350=8.3500实验的8.35≠8.350≠8.35002.有效数字的位数与被测量的大小及仪器的精密度有关。3.第一个非零数字前的零不是有效数字，第一个非零数字开始的所有数字都是有效数字。如2.327kg有4位有效数字,其中7是存疑数字;220v有3位有效数字,其中0是存疑数字;0.002cm有1位有效数字,其中2是存疑数字;0.00mm有1位有效数字,其中末位0是存疑数字.\n4.单位的变换不能改变有效数字的位数。如2.327kg=2.327×10-3t=2327g=2.327×106mg5.实验中要求尽量使用科学计数法（小数点前仅写出一位非零数字）表示数据。数学上改变了有效数字的位数科学计数法不改变有效数字的位数\n有效数字运算规则1.采用四舍五入法对有效数字进行取舍.2.加减法:结果的可疑位与参与运算数据中存疑位数量级最高的对齐.例如:2.327+10.8=13.1272.327+10.8=13.13.乘除法:结果的有效数字的位数与参与运算数据中有效数字位数最少的相同.例如：2327×108=2513162327×108=2.51×1054.π、g等或者在公式中出现的常数可视为无穷多位，使用时所取的位数不少于参与运算数据中位数最少的。例如：S=πD2/4=3.142×2.3272÷4或者=3.1416×2.3272÷4\n直接测量量有效数字的确定如:1/50mm的游标卡尺的游标分度值0.02mm,因此,记录测量结果时,最后一位有效数字应记录到1/100mm位.1．游标类量具，有效数字最后一位与游标分度值对齐.\n2．数显仪表及有十进步式标度盘的仪表（电阻箱、电桥、电位差计、数字电压表等）一般应直接读取仪表的示值。\n3.米尺、指针式仪表这类的刻度式仪器，估读到最小分度值的1/10（不能估读到0.1分度以下，即不能估读到0.01分度）.5.737mm\n4.如下图，尺子只标出整刻度和半刻度线时,则认为半刻度线没有标出，仍然按照3中的方式估读。因为图中的最小分度值为1，红色部分的长度估读为1.1或1.2都可以。123\n测量结果有效数字的取舍对于测量结果（单位）的有效数字，要先确定不确定度的有效数字，再确定最佳估计值的有效数字。按国家技术规范,测量不确定度的有效数字最多不超过2位。在学生实验中，由于测量次数有限及其它因素，结果的准确性有限，故可以只取1位有效数字，多余数字按照1/3(3舍4入)法则进行取舍。如：扩展不确定度U为0.324mm，保留两位有效数字，U=0.33mm；保留一位有效数字，U=0.3mm1.不确定度的有效数字\n2.最佳估计值的有效数字最佳估计值的最后一位必须和不确定度的末位对齐。多余的数字，按4舍5入规则进行取舍。如：V=5836.340lmm3，U=4.2mm3则最后结果的表达式应为3.作为中间计算结果时，直接测量量的不确定度，可以取不少于3位有效数字或者全部保留,以避免积累舍入误差。\n五综合举例【例题】用单摆测重力加速度的公式为。现用最小读数为1/100s的电子秒表测量周期T五次，其周期的测量值为2.001，2.004，1.997，1.998，2.000（单位：s）；用Ⅱ级钢卷尺测摆长L一次，L=100.00cm。试求重力加速度g及合成不确定度，并写出结果表达式。注：每次周期值是通过测量100个周期获得，每测100个周期要按两次表，由于按表时超前或滞后造成的最大误差是0.5s；Ⅱ级钢卷尺测量长度L的示值误差为（L是以米为单位得到的数值），由于卷尺很难与摆的两端正好对齐，在单次测量时引入的误差极限为±2mm。\n1.计算直接测量量的最佳估计值T的估计值：L的估计值：2.计算间接测量量g的最佳估计值\n3.计算直接测量量的不确定度（1）计算摆长L的测量不确定度相应的不确定度为测量时卷尺不能对准L两端造成的仪器误差相应的不确定度为L的合成不确定度为仪器的示值误差L的相对不确定度摆长只测了一次，只考虑B类不确定度,有两个分量。\n（2）计算周期T的测量不确定度T的A类不确定度T的B类不确定度有两个分量，一个与仪器误差对应，一个与按表超前或滞后造成的误差对应因比小得多，可略去，故合成不确定度为T的相对不确定度分别是\n扩展不确定度为4.计算间接测量量g的不确定度由于是积商关系，根据相对合成不确定公式有g的不确定度为5.写出结果表达式或\n六记录实验数据的基本要求使用表格记录实验数据——列表法要在表的上方注明表的名称；结构要尽量简单，表格线条要清晰，便于记录运算和检查；要注明各物理量的符号和单位；数据的有效数字要能正确反映测量的误差。数据表格一般需要自己设计。序号12345678910U/V0.01.02.03.04.05.06.07.08.09.0I/mA0.02.04.06.17.99.711.813.816.017.9表一电阻伏安特性数据表\n七处理实验数据的几种方法作图法伏安曲线要求：1.正确标注数据点一般同一条曲线上的数据点用同一种符号标注，不同曲线上的坐标点选用不同的符号，如“×、○、+”等。2.要有图名和说明应在图纸上标出图的名称，有关符号的意义和特定实验条件。3.可以使用一些数学、统计软件进行作图。\n12120在进行测量电阻实验时，测得数据中电压和电流的最大值均不超过2，其中有一组数为U=1.81V，I=1.52mA。要求作出电阻的I~U曲线，并给你如下一张坐标纸。如何充分、合理地利用坐标纸？如何正确地表示这一组U，I值？I(mA)U(V)+1.81.5+I~U曲线\n2112U(V)I(mA)0(1.81,1.52)\n逐差法就是将2q(q≥2)个测量数据按如下的方式分为前后两组：x1,x2,…xq；xq+1,xq+2…x2q然后相隔q项求差值：yj=xj+q-xj最后求平均值：逐差法逐差法的适用条件：1.物理量y与x间的函数关系是线性的；2.自变量是等间距变化的；3.要有偶数个测量数据。\nX(g)1.002.003.004.005.006.007.008.009.0010.00Y(cm)2.004.016.057.859.7011.8313.7516.0217.8519.94iXii+5Xi+5△X11.0066.005.0022.0077.005.0033.0088.005.0044.0099.005.0055.001010.005.00iYii+5Yi+5△Y12.00611.839.8324.01713.759.7436.05816.029.9747.85917.8610.0159.701019.9410.24下表记录了测量弹簧倔强系数的数据，试用逐差法求算弹簧的倔强系数。表中X代表砝码质量，Y代表弹簧的伸长量。逐差法举例1）对X进行分组并求逐差2）对Y进行分组并求逐差\n5.009.9581.99163）求倔强系数逐差法举例\n八实验报告常见问题\n\n