大学物理总复习下 39页

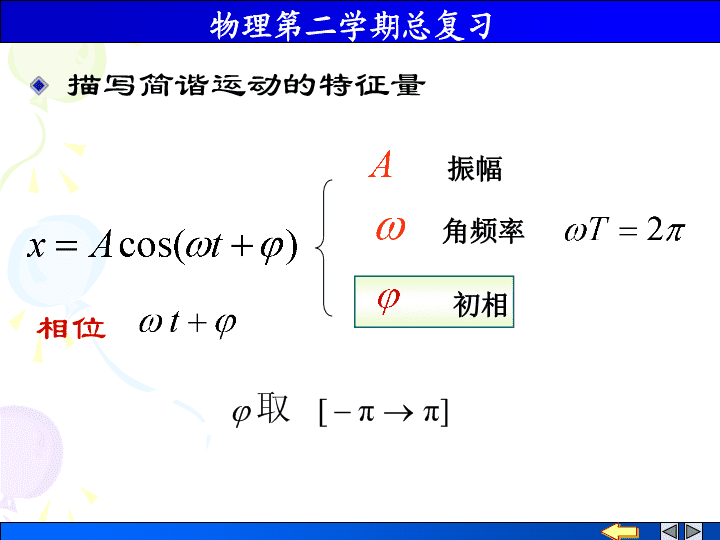
简谐运动简谐运动的合成阻尼振动、受迫振动(共振)机械振动描述；旋转矢量图动力学方程；能量\n描写简谐运动的特征量相位角频率振幅初相\n图像描述0相量图了解各特征量在图线上的意义旋转矢量图\n0相量图\n练习：已知物体作简谐运动的图线，试根据图线写出其振动方程\n振动能量振子：动能弹簧：弹性势能1.构成2.公式3.特点——机械能守恒\n同方向同频率相位差：同相；反相简谐运动的合成\n1.求振动方程习题17.2，17.3例题17.12.能量分析习题：习题17.7\n物理量；波函数；图形；能量；传播规律波的描述波的叠加多普勒效应机械波的产生及特点机械波干涉；驻波\n波长周期频率波速1.描述波的物理量每一质元的动能和弹性势能是同相变化的2.波的能量的特点\n3.熟练掌握求解波函数步骤P*O4.能从波形曲线中读出有用信息\n波函数振动方程已知：点X0振动方程求：波函数\n干涉:波的相干叠加波源的相位差波程差1)相位差*5.波的叠加：干涉、驻波参见习题18.15\n其他振动始终加强振动始终减弱干涉加强和减弱的条件\n2.特点：一种特殊的干涉（书P222－223）4.驻波的计算驻波方程（关键：反射波的波函数）1.形成3.半波损失（书P223）——实质；条件驻波\n\n练习：已知平面简谐波的波函数为求：波的频率，波速，波长，周期(A,a,b为正)\n练习：一平面波沿－x方向传播，u=6m/s,若x=－3m处的p点振动曲线如图。求：（1）P点的振动方程（2）平面波的波函数。\n波动方程练习：一平面简谐波向ox轴　负向传播，已知其　时的　波形曲线，设波速为　，振幅为Ａ，波长为，求\n练习：设弦线上入射波波动方程为在　　处发生反射，反射点为一固定端求（１）反射波的波动方程（２）合成波即驻波的方程，并求出波节和波腹的位置\n一、光源发光机制相干光的获得二、双缝干涉三、光程半波损失四、薄膜干涉（等厚；等倾）五、迈克耳孙干涉仪光的干涉\n光的干涉的相关计算②计算光程差①找出两束相干光步骤：③干涉减弱干涉加强\nSdDxOP干涉条纹I光强分布（1）双缝干涉：习题：19.5、19.9求各级角位移、线位移及间距\n减弱加强p干涉条件：\n（2）薄膜干涉③计算光程差①找到薄膜②明确相干光增透膜和增反膜习题：19.12、19.13\n劈尖的干涉条件：明纹暗纹（明纹）（暗纹）\n劈尖劈尖夹角变小/大，条纹向_____移动，条纹间距_____习题：19.10\nn1nen2如图，薄膜干涉中若反射光消失,(A)(1)2ne=k,(2)2ne=k.(B)(1)2ne=k+/2,(2)2ne=k+/2.(C)(1)2ne=k－/2,(2)2ne=k.(D)(1)2ne=k,(2)2ne=k－/2.则当n1＜n＜n2时,应满足条件(1)；当n1＜n＞n2时应满足条件(2).条件(1),条件(2)分别是\n已知：问：有多少条明纹？单色光入射空气劈尖，且有\n\n一、光的衍射（现象；分类；惠－菲原理）二、单缝衍射三、圆孔衍射四、光栅衍射五、X射线衍射（半波带法）（光栅方程；缺级；光谱）（瑞利判据；最小分辨角；分辨率）（布拉格公式）\n暗纹中心明纹中心中央明纹中心1.注意：不取0单缝衍射：各级角位移、线位移、间距\n例题20.1、习题20.3\n光栅衍射光栅构造：光栅常数光栅条纹定性：定量：单缝衍射＋多缝（光束）干涉光栅方程＋缺级条件\n缺级条件：光栅方程(明纹位置)\nsin0I单I0单-2-112(/a)单缝衍射IN2I0单048-4-8sin(/d)光栅衍射sin04-8-48(/d)多光束干涉主极大\n单缝衍射中，当衍射角满足时阵面可分为_______个半波带。若将缝宽缩小一半，则此位置将变为第____级____条纹61明练习：对应位置为第____级______条纹，此时单缝的波3暗\n可见平行光入射单缝，已知缝宽0.5mm，透镜，在离屏上中央明纹中心距离1.5mm处的P点为某级亮纹中心，求：（1）入射光波长（2）P点条纹级数和及其对应的衍射角（3）P点对应的波阵面可分为几个半波带（4）中央明纹的宽度\n解（1）（2）（3）因此，可以看到8级光谱，15条明纹。λ＝600nm的单色光垂直入射到光栅上，第二级明纹出现在sin＝0.2处，第四级缺级。求:（1）光栅常数a＋b＝？（2）最小缝宽a＝？（3）对应最小缝宽可以看到几条明纹？