大学物理9-213091 18页

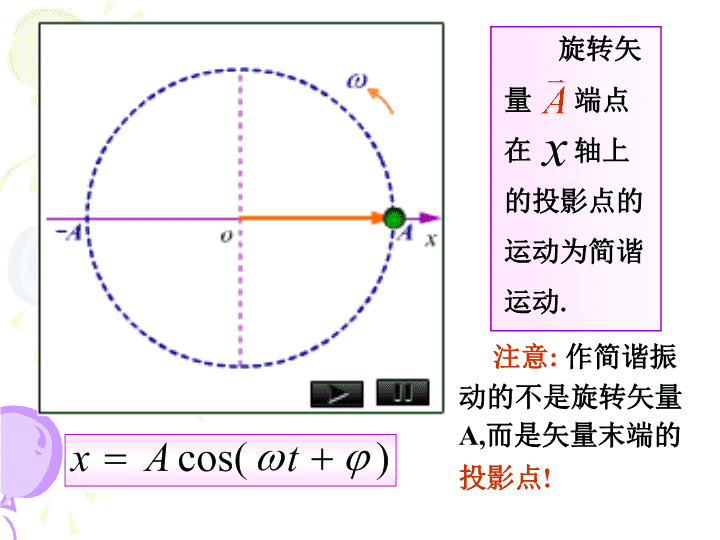
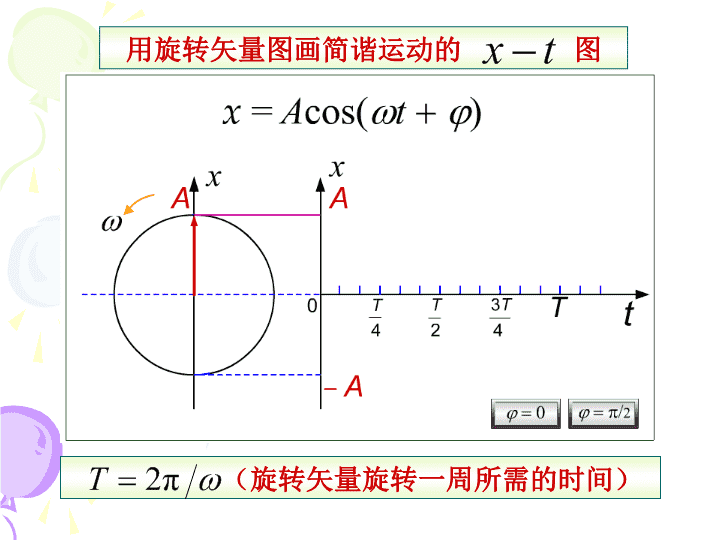
§9-2旋转矢量简谐运动的表示法有多种，重要的是把简谐运动的三要素表示出来.常用的有:（一）三角函数表示：x=Acos(t+)（三）旋转矢量法本节着重介绍旋转矢量表示法.（二）图像法\n旋转矢量端点在轴上的投影点的运动为简谐运动.注意:作简谐振动的不是旋转矢量A,而是矢量末端的投影点!旋转矢量表示简谐运动\n（旋转矢量旋转一周所需的时间）用旋转矢量图画简谐运动的图旋转矢量图与三角函数图的对应关系\n旋转矢量法的作用直观表示振幅A、角频率和相位(t+)及初相；直接确定简谐振动的位移x、速度v、加速度a；旋转矢量法的作用\n讨论相位差：表示两个相位之差.1）对同一简谐运动，相位差可以给出两运动状态间变化所需的时间.讨论相位差\n2）对于两个同频率的简谐运动，相位差表示它们间步调上的差异.（解决振动合成问题）同相反相>0,x1落后x2<0,x1超前x2用相位差比较步调的差异\n例1(P8)一质量为的物体作简谐运动，其振幅为，周期为，起始时刻物体在处，向轴负方向运动（如图）.试求（1）时，物体所处的位置和所受的力；解设例1(P8)\n即\n代入上式得\n（2）由起始位置运动到处所需要的最短时间.解法一设由起始位置运动到处所需要的最短时间为\n解法二起始时刻时刻\n例2如图所示，一轻弹簧的右端连着一物体，弹簧的劲度系数，物体的质量.（1）把物体从平衡位置向右拉到处停下后再释放，求简谐运动方程；（3）如果物体在处时速度不等于零，而是具有向右的初速度，求其运动方程.（2）求物体从初位置运动到第一次经过处时的速度；0.05例2\n解（1）由旋转矢量图可知\n解由旋转矢量图可知（负号表示速度沿轴负方向）（2）求物体从初位置运动到第一次经过处时的速度；\n解（3）如果物体在处时速度不等于零，而是具有向右的初速度，求其运动方程.因为，由旋转矢量图可知\n例3一质点作周期为T的简谐振动，质点由平衡位置向x轴正方向运动到最大位移一半处所需的最短时间为(A)T/2(B)T/4(C)T/8(D)T/12解:(用矢量图法求解)=t=/6=2/T∴t=T/12MωA/2NOAx例3\n例4一质点作简谐振动，=4Hz,振幅A=2cm.当t=0时,质点位于x=1cm处，并且向x轴正方向运动,求振动表达式.解法1:（用解析法求解）例4\n解法2:（用矢量图法求解）作半径为2cm的圆.由t=0时，质点位于x=1cm处知:旋转矢量端点可位于图中A、B两处.又由质点向x轴正方向运动可得，初始时刻旋转矢量端点应位于B处.AB12Ox例4解法2旋转矢量法求解