大学物理9-213223 24页

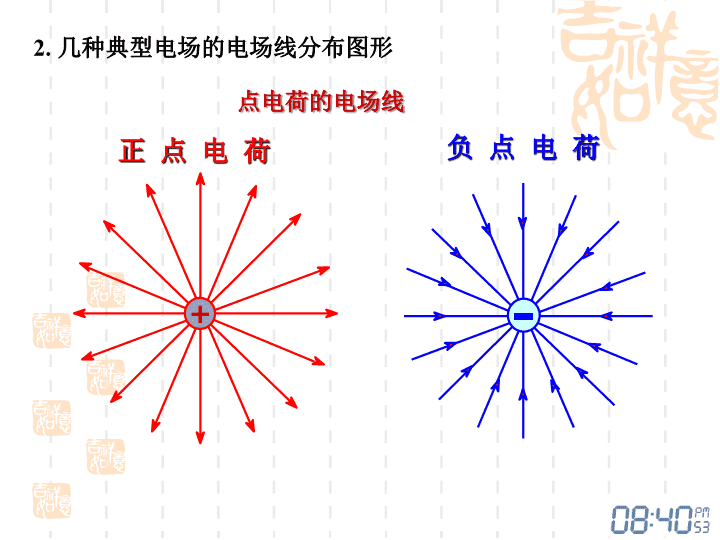
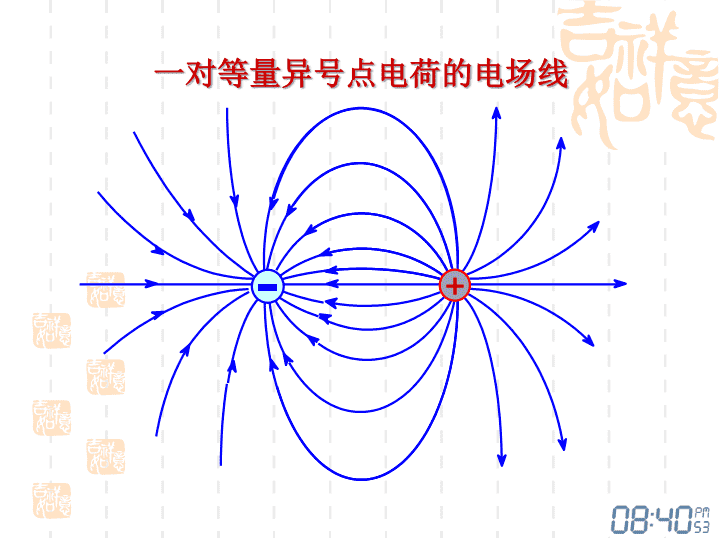
9-3电通量高斯定理一、电场线electricfieldline描述电场分布情况的曲线。1.电场线：⑴曲线上每一点的切线方向表示该点电场强度E方向⑵曲线的疏密表示该点处场强E的大小。即：垂直通过单位面积的电场线条数，在数值上就等于该点处电场强度的大小。dS－电场线密度\n点电荷的电场线正点电荷+负点电荷2.几种典型电场的电场线分布图形\n一对等量异号点电荷的电场线+\n一对等量正点电荷的电场线++\n一对不等量异号点电荷的电场线\n带电平行板电容器的电场线++++++++++++3.电场线的性质：(2)起于正电荷，止于负电荷，不会在无电荷处中断。(3)不会自行构成闭合曲线，任意两条电场线在无电荷处不会相交。(1)可用电场线的疏密程度来描述电场强度的大小：电场线密处，场强大；电场线疏处，场强小。\n二、电通量(electricflux)e1.e的定义2.e的计算(1)均匀电场中通过任一平面的电通量垂直平面与平面夹角通过电场中任一曲面的电场线总数定义为通过该面的电通量。\n(2)非均匀电场中通过任意曲面的电通量S为封闭曲面穿出穿入相切\n解：例1．计算均匀电场中一圆柱面的电通量。已知及=0\n1.求均匀电场中一闭合半球面的电通量。2.在均匀电场中，过YOZ平面内面积为S的电通量。课堂练习\n三、高斯定理Gausstheorem高斯定理讨论的是:封闭曲面的电通量与该曲面内包围的电荷之间的关系R1、点电荷的情况1)通过以点电荷为球心,半径为R的球面的电通量+q\n2)点电荷不位于球面的中心3)任意形状封闭曲面4)点电荷位于封闭曲面外+qR+qR+q\n若场源为点电荷系，其中n个点电荷在S内，m个点电荷在S外2、点电荷系的情况\n3、静电场的高斯定理Gausstheorem(4)反映了静电场是“有源场”(1)不仅适用静电场，也适用变化的电场。(2)高斯面上的电场强度为所有内外电荷的总电场强度(3)仅高斯面内的电荷对高斯面的电场强度通量有贡献在真空中的静电场内，通过任一闭合曲面的电通量等于这闭合曲面所包围的电荷量的代数和除以0讨论\n在点电荷+q和-q的静电场中，做如下的四个闭合面求通过各闭合面的电通量.讨论将从移到点电场强度是否变化？穿过高斯面的有否变化？*\n四、高斯定理的应用常见的电量分布的对称性(均匀带电)球对称柱对称面对称球体球面球壳点电荷（无限长）柱体柱面带电线（无限大）平板平面电荷的分布具有某种对称性的情况下利用高斯定理求解较为方便\n其步骤为：（1）对称性分析；（2）根据对称性选择合适的高斯面；（3）应用高斯定理计算.大小：闭合面通过待求场点，且包围部分或者全部电荷形状：由场的对称行决定（曲面上各部分要么与场强E平行，要么与场强E垂直，且与E垂直的那部分曲面上各点E相等）。则\n例1.求电量为q、半径为R的均匀带电球体的场强分布。(1)分析对称性：E沿径向。(2)取高斯面：球面。(3)计算通量、场强oER讨论：均匀带电球面E内=0\n例2.求无限大带电平面(均匀带电+)的场强。(1)分析对称性：E垂直带电平面。(2)取高斯面：柱面。(3)计算通量、场强\n讨论无限大带电平面的电场叠加问题\n+++++例3无限长均匀带电直线的电场强度选取闭合的柱形高斯面无限长均匀带电直线，单位长度上的电荷，即电荷线密度为，求距直线为r处的电场强度.解:对称性分析：轴对称+讨论②有限长带电柱体能不能用高斯定理求场强？③非均匀带电柱面能不能用高斯定理求场强？①无限长带电柱体是否仍可用高斯定理求场强？\n例4.两同心均匀带电球面，半径分别为R1和R2，带电量分别为+q1和-q2，求其电场强度分布。r解:场强分布球对称，由高斯定理求解0R1R2+q1-q2\n重点和难点：★正确理解高斯定理★高斯定理的应用电场对称性分析。选取高斯面。应用高斯定理求场强。计算通过高斯面的电通量。\n本次作业：完成作业2下次上课内容：§9-4～§9-6