大学物理作业答案(下) 33页

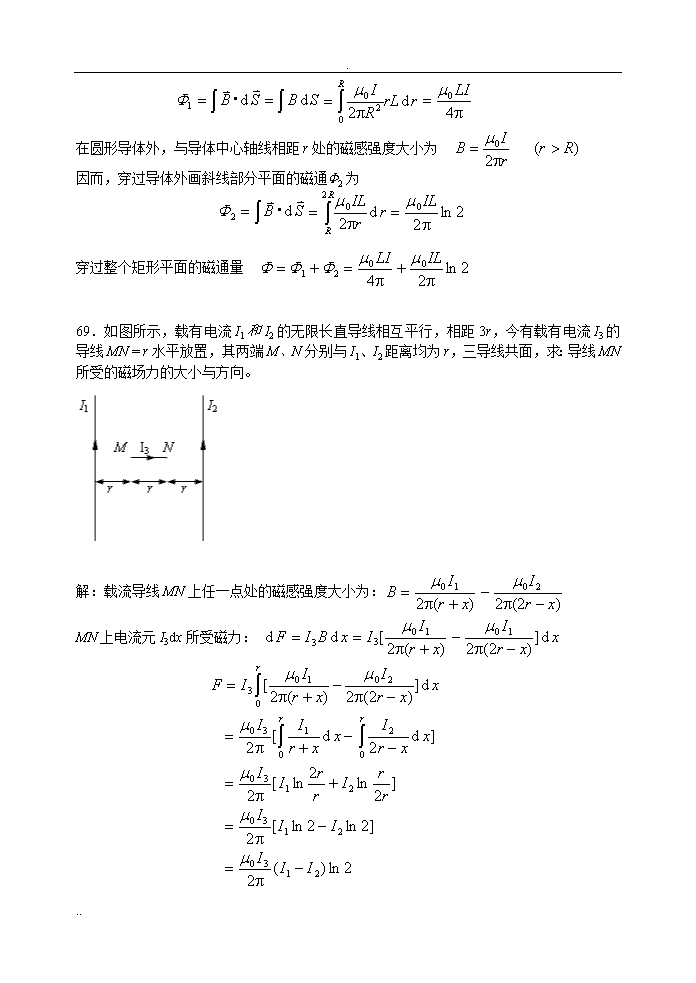
.65．如图所示，几种载流导线在平面内分布，电流均为I，求：它们在O点的磁感应强度。1方向垂直纸面向外2方向垂直纸面向里3方向垂直纸面向外66．一半径为R的均匀带电无限长直圆筒，电荷面密度为σ，该筒以角速度ω绕其轴线匀速旋转。试求圆筒内部的磁感应强度。解：如图所示，圆筒旋转时相当于圆筒上具有同向的面电流密度i，作矩形有向闭合环路如图中所示．从电流分布的对称性分析可知，在上各点的大小和方向均相同，而且的方向平行于，在和上各点的方向与线元垂直，在,上各点．应用安培环路定理可得圆筒内部为均匀磁场，磁感强度的大小为，方向平行于轴线朝右．67．在半径为R的长直金属圆柱体内部挖去一个半径为r的长直圆柱体，两柱体轴线平行，其间距为a（如图）。今在此导体内通以电流I，电流在截面上均匀分布，求：空心部分轴线上O¢点的磁感应强度的大小。..\n.解：68．一无限长圆柱形铜导体,半径为R,通以均匀分布的I今取一矩形平面S（长为L，宽为2R），位置如图，求：通过该矩形平面的磁通量。解：在圆柱体内部与导体中心轴线相距为r处的磁感强度的大小，由安培环路定律可得：因而，穿过导体内画斜线部分平面的磁通F1为..\n.在圆形导体外，与导体中心轴线相距r处的磁感强度大小为因而，穿过导体外画斜线部分平面的磁通F2为穿过整个矩形平面的磁通量69．如图所示，载有电流I1和I2的无限长直导线相互平行，相距3r，今有载有电流I3的导线MN=r水平放置，其两端M、N分别与I1、I2距离均为r，三导线共面，求：导线MN所受的磁场力的大小与方向。解：载流导线MN上任一点处的磁感强度大小为：MN上电流元I3dx所受磁力：..\n.若，则的方向向下，，则的方向向上70．一线圈由半径为0.2m的1/4圆弧和相互垂直的二直线组成，通以电流2A，把它放在磁感应强度为0.5T的垂直纸面向里的均匀磁场中，求(1)线圈平面与磁场垂直时，圆弧AB所受的力；(2)线圈正法线方向和磁场成30°时，线圈所受的磁力矩。解：(1)圆弧AC所受的磁力：在均匀磁场中AC通电圆弧所受的磁力与通有相同电流的直线所受的磁力相等，故有FAC=N方向：与AC直线垂直，与OC夹角45°，如图．(2)磁力矩：线圈的磁矩为本小问中设线圈平面与成60°角，则与成30°角，有力矩M=1.57×10-2N·m方向：力矩将驱使线圈法线转向与平行.71．有一无限大平面导体薄板，自上而下通有电流。已知其电流面密度为i。（1）试求：板外空间任一点的磁感应强度；（2）有一质量为m、带电量为q（q>0）的粒子，以速度v沿平板法线方向向外运动，求：带电粒子最初至少在距板什么位置处才不与大平板碰撞，需经多长时间才能回到初始位置？解：(1)由安培环路定理：(大小)方向：在板右侧垂直纸面向里(2)由洛伦兹力公式可求(至少从距板R处开始向外运动)返回时间..\n.72．如图所示，半径为R的木球上绕有密集的细导线，线圈平面彼此平行，且以单层线圈覆盖半个球面，设线圈的总匝数为N，通过线圈的电流为I。求：球心O处的磁感应强度。x解：坐标选取如图：其中=方向沿x轴正向73．一电子以速度v垂直地进入磁感应强度为B的均匀磁场中（如图）。求：此电子在磁场中运动轨道所围的面积内的磁通量示多少？解：∵半径，∴..\n.磁通量74．一半径为R=1.0cm的无限长1/4圆柱形金属薄片，沿轴向通以电流I=10.0A的电流，设电流在金属片上均匀分布，试求：圆柱轴线上任意一点P的磁感应强度。解：取dl段，其中电流为在P点选坐标如图,1.8×10-4T方向，a=225°，a为与x轴正向的夹角．75．一半径为R的圆筒形导体通以电流I，筒壁很薄，可视为无限长，筒外有一层厚为d，磁导率为m的均匀顺磁性介质，介质外为真空。画出此磁场的H—r曲线及B—r曲线（要求：在图上标明各曲线端点的坐标及所代表的函数值）..\n.76．螺绕环中心周长l=30cm，横截面S=1.0cm2，环上紧密地绕有N=300匝的线圈。当导线中电流I=32mA，通过环截面的磁通量F=2.0´10-6Wb，求：铁芯的磁化率cm。解：B=F/S=2.0×10-2T32A/m6.25×10-4T·m/A49677．均匀带电刚性细杆AB，线电荷密度为l，绕垂直于直线的轴O以w角速度匀速转动(O点在细杆AB延长线上)．求：(1)O点的磁感强度；(2)系统的磁矩；(3)若a>>b，求B0及pm．1..\n.方向垂直纸面向里23..\n.78．如图所示,两个共面的带动圆环,其内外径分别为R1、R2和R2、R3，外面的圆环以每秒钟n2转顺时针转动，里面的圆环一每秒钟n1转的转速反时针转动，若二者电荷面密度均为σ，求：n1和n2的比值多大时，圆心处磁感应强度为零。解：(1)在内圆环上取半径为r宽度为dr的细圆环，其电荷为由于转动而形成的电流di在O点产生的磁感强度为其方向垂直纸面向外．(2)整个内圆环在O点产生的磁感强度为其方向垂直纸面向外．(3)同理得外圆环在O点产生的磁感强度其方向垂直纸面向里．(4)为使O点的磁感应强度为零，B1和B2的量值必须相等，即于是求得n1和n2之比79．两个半径分别为R和r的同轴圆形线圈相距x，且R>>r，x>>R．若大线圈通有电流I而小线圈沿x轴方向以速率v运动，试求x=NR时(N为正数)小线圈回路中产生的感应电动势的大小．..\n.答：由题意，大线圈中的电流在小线圈回路处产生的磁场可视为均匀的．故穿过小回路的磁通量为由于小线圈的运动，小线圈中的感应电动势为当时，小线圈回路中的感应电动势为80．一导线弯成如图形状，放在均匀磁场中，的方向垂直图面向里．∠bcd=60°，bc=cd=a．使导线绕轴OO＇旋转，如图，转速为每分钟n转．计算eOO¢＇．Bcbd解：，∴81．电量Q均匀分布在半径为a、长为L(L>>a)的绝缘薄壁长圆筒表面上，圆筒以角速度绕中心轴线旋转。一半径为2a、电阻为R..\n.的单匝圆形线圈套在圆筒上（如图所示）。若圆筒转速按照0(1－t/t0)的规律（和t0是已知常数）随时间线性地减少，求：圆形线圈中感应电流的大小和方向。解：筒以w旋转时，相当于表面单位长度上有环形电流，它和通电流螺线管的nI等效．按长螺线管产生磁场的公式，筒内均匀磁场磁感强度为：(方向沿筒的轴向)筒外磁场为零．穿过线圈的磁通量为：在单匝线圈中产生感生电动势为感应电流i为i的流向与圆筒转向一致．82．两根平行放置相距为2a的无限长载流直导线，其中一根通以稳恒电流I0，另一根通以交变电流i=I0cost．两导线间有一与其共面的矩形线圈，线圈的边长分别为l和2b，l边与长直导线平行，且线圈以速度垂直直导线向右运动(如图)．当线圈运动到两导线的中心位置(即线圈中心线与距两导线均为a的中心线重合)时，两导线中的电流方向恰好相反，且i=I0，求：此时线圈中的感应电动势．解：设动生电动势和感生电动势分别用e1和e2表示，则总电动势e为e=e1+e2，..\n.∵此刻i=I0，则∴e1=0e=e2①由①式，得∵i=I0时，(k=1，2，…)∴=083．有一很长的长方形U形导轨，与水平面成q角，裸导线ab可在导轨上无摩擦地下滑，导轨位于磁感应强度B垂直向上的均匀磁场中，如图所示。设导线ab的质量为m，电阻为R，长度为l，导轨的电阻略去不计，abcd形成电路，t=0时，v=0，试求：导线ab下滑的速度v与时间t的函数关系。解：ab导线在磁场中运动产生的感应电动势abcd回路中流过的电流ab载流导线在磁场中受到的安培力沿导轨方向上的分力为：由牛顿第二定律：..\n.令，则利用t=0，v=0有∴84．无限长直导线载有电流I，其旁放置一段长度为l与载流导线在同一平面内且成的导线。计算当该导线在平面上以垂直于载流导线的速度v平移到该导线的中点距载流导线为a时，其上的动生电动势，并说明其方向。解：在dl处但∴其中，方向从1→2．？？85．一无限长直导线通有电流，一矩形线圈与长直导线共面放置，其长边与导线平行，如图所示。求：（1）矩形线圈中感应电动势的大小及方向；（2）导线与线圈的互感系数。..\n.86.两个共轴圆线圈，半径分别为和，匝数分别为和，两者相距．设小线圈的半径很小，小线圈处的磁场近似地可视为均匀，求：两线圈的互感系数．并讨论时的情况.答：设大线圈中通以电流，匝线圈形成的环电流在轴线上产生的磁感应强度为小线圈的面积为，大线圈通过一匝小线圈的磁通量为在小线圈中产生的磁通链数为互感系数为..\n.当两线圈相距很近时，时，互感系数约为？？87．半径为r的小绝缘圆环，置于半径为R的大导线圆环中心，二者在同一平面内，且r<