大学物理课后习题 15页

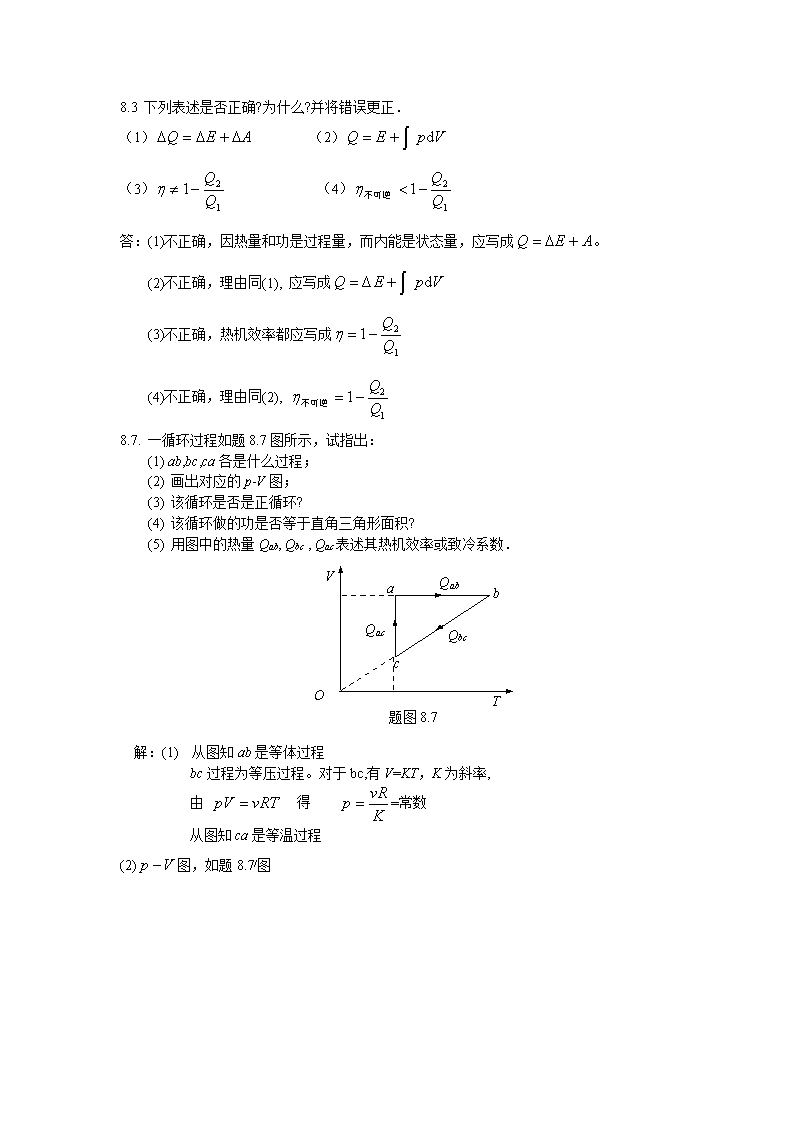
8.3下列表述是否正确?为什么?并将错误更正．（1）（2）（3）（4）答：(1)不正确，因热量和功是过程量，而内能是状态量，应写成。(2)不正确，理由同(1),应写成(3)不正确，热机效率都应写成(4)不正确，理由同(2),8.7.一循环过程如题8.7图所示，试指出：(1)ab,bc,ca各是什么过程；(2)画出对应的p-V图；(3)该循环是否是正循环?(4)该循环做的功是否等于直角三角形面积?(5)用图中的热量Qab,Qbc,Qac表述其热机效率或致冷系数．VOTabcQacQabQbc题图8.7解：(1)从图知ab是等体过程bc过程为等压过程。对于bc,有V=KT，K为斜率,由得=常数从图知ca是等温过程(2)图，如题8.7/图\npOVabc题图8.7/(3)从图题图8.7/知该循环是逆循环(4)该循环作的功不等于直角三角形面积，因为直角三角形不是图中的图形．(5)8.121mol单原子理想气体从300K加热到350K，问在下列两过程中吸收了多少热量?增加了多少内能?对外做了多少功?(1)容积保持不变；(2)压力保持不变。解：(1)等体过程由热力学第一定律得吸热对外作功(2)等压过程吸热内能增加对外作功8.13一个绝热容器中盛有摩尔质量为Mmol，比热容比为γ的理想气体，整个容器以速度u运动，若容器突然停止运动，求气体温度的升高量(设气体分子的机械能全部转变为内能)。解：整个气体有序运动的能量为，转变为气体分子无序运动使得内能增加，温度变化\n8.140.01m3氮气在温度为300K时，由1MPa(即1atm)压缩到10MPa。试分别求氮气经等温及绝热压缩后的(1)体积；(2)温度；(3)各过程对外所做的功。解：(1)等温压缩T=300K由求得体积m3对外作功(2)绝热压缩由绝热方程 由绝热方程得热力学第一定律，所以\n，9.7长=15.0cm的直导线AB上均匀地分布着线密度=5.0x10-9C·m-1的正电荷．试求：(1)在导线的延长线上与导线B端相距=5.0cm处点的场强；(2)在导线的垂直平分线上与导线中点相距=5.0cm处点的场强．解：如题9.7图所示(1)在带电直线上取线元，其上电量在点产生场强为题9.7图用，,代入得方向水平向右(2)同理方向如题9.7图所示由于对称性，即只有分量，∵\n以,,代入得，方向沿轴正向9.8一个半径为的均匀带电半圆环，电荷线密度为,求环心处点的场强．解:如9.8图在圆上取题9.8图，它在点产生场强大小为方向沿半径向外则积分∴，方向沿轴正向．9.10(1)点电荷位于一边长为a的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?解:(1)由高斯定理立方体六个面，当在立方体中心时，每个面上电通量相等\n∴各面电通量．(2)电荷在顶点时，将立方体延伸为边长的立方体，使处于边长的立方体中心，则边长的正方形上电通量对于边长的正方形，如果它不包含所在的顶点，则， 如果它包含所在顶点则．如题9.10图所示．题9.10图9.12半径为和(＞)的两无限长同轴圆柱面，单位长度上分别带有电量和-,试求:(1)＜；(2)＜＜；(3)＞处各点的场强．解:高斯定理取同轴圆柱形高斯面，侧面积则对(1)(2)∴沿径向向外(3)∴题9.17图9.17如题9.17图所示，在，两点处放有电量分别为+,-的点电荷，间距离为2\n，现将另一正试验点电荷从点经过半圆弧移到点，求移动过程中电场力作的功．解:如题9.17图示∴9.18如题9.18图所示的绝缘细线上均匀分布着线密度为的正电荷,两直导线的长度和半圆环的半径都等于．试求环中心点处的场强和电势．解:(1)由于电荷均匀分布与对称性，和段电荷在点产生的场强互相抵消，取则产生点如图，由于对称性，点场强沿轴负方向题9.18图［］(2)电荷在点产生电势，以同理产生\n半圆环产生∴题10.9图10.9如题10.9图所示，、为长直导线，为圆心在点的一段圆弧形导线，其半径为．若通以电流，求点的磁感应强度．解：如题10.9图所示，点磁场由、、三部分电流产生．其中产生产生，方向垂直向里段产生，方向向里∴，方向向里．10.10在真空中，有两根互相平行的无限长直导线和，相距0.1m，通有方向相反的电流，=20A,=10A，如题10.10图所示．，两点与导线在同一平面内．这两点与导线的距离均为5.0cm．试求，两点处的磁感应强度，以及磁感应强度为零的点的位置．题10.10图解：如题10.10图所示,方向垂直纸面向里\n(2)设在外侧距离为处则解得题10.14图10.14两平行长直导线相距=40cm，每根导线载有电流==20A，如题10.14图所示．求：(1)两导线所在平面内与该两导线等距的一点处的磁感应强度；(2)通过图中斜线所示面积的磁通量．(==10cm,=25cm)．解：(1)T方向纸面向外(2)取面元题10.22图10.22如题10.22图所示，在长直导线内通以电流=20A，在矩形线圈中通有电流=10A，与线圈共面，且，都与平行．已知=9.0cm,=20.0cm,\n=1.0cm，求：(1)导线的磁场对矩形线圈每边所作用的力；(2)矩形线圈所受合力和合力矩．解：(1)方向垂直向左，大小同理方向垂直向右，大小方向垂直向上，大小为方向垂直向下，大小为(2)合力方向向左，大小为合力矩∵线圈与导线共面∴．10.25一长直导线通有电流＝20A，旁边放一导线，其中通有电流=10A，且两者共面，如题10.25图所示．求导线所受作用力对点的力矩．解：在上取，它受力向上，大小为对点力矩方向垂直纸面向外，大小为\n题10.25图题11.6图11.6如题11.6所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以的变化率增大，求：(1)任一时刻线圈内所通过的磁通量；(2)线圈中的感应电动势．解:以向外磁通为正则(1)(2)题11.11图11.11导线长为，绕过点的垂直轴以匀角速转动，=磁感应强度平行于转轴，如图11.11所示．试求：（1）两端的电势差；（2）两端哪一点电势高?解:(1)在上取一小段则\n同理∴(2)∵即∴点电势高．题11.12图11.12如题11.12图所示，长度为的金属杆位于两无限长直导线所在平面的正中间，并以速度平行于两直导线运动．两直导线通以大小相等、方向相反的电流，两导线相距2．试求：金属杆两端的电势差及其方向．解：在金属杆上取距左边直导线为，则∵∴实际上感应电动势方向从，即从图中从右向左，∴13.7在杨氏双缝实验中，双缝间距=0.20mm，缝屏间距＝1.0m，试求：(1)若第二级明条纹离屏中心的距离为6.0mm，计算此单色光的波长；(2)相邻两明条纹间的距离．解:(1)由知，，∴(2)13.8在双缝装置中，用一很薄的云母片(n=1.58)覆盖其中的一条缝，结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明纹的位置．若入射光的波长为5500，求此云母片的厚度．\n解:设云母片厚度为，则由云母片引起的光程差为按题意∴13.12在折射率=1.52的镜头表面涂有一层折射率=1.38的Mg增透膜，如果此膜适用于波长=5500的光，问膜的厚度应取何值?解:设光垂直入射增透膜，欲透射增强，则膜上、下两表面反射光应满足干涉相消条件，即∴令，得膜的最薄厚度为．当为其他整数倍时，也都满足要求．13.13如题13.13图，波长为6800的平行光垂直照射到＝0.12m长的两块玻璃片上，两玻璃片一边相互接触，另一边被直径=0.048mm的细钢丝隔开．求：(1)两玻璃片间的夹角?(2)相邻两明条纹间空气膜的厚度差是多少?(3)相邻两暗条纹的间距是多少?(4)在这0.12m内呈现多少条明条纹?题13.13图解:(1)由图知，，即故(弧度) (2)相邻两明条纹空气膜厚度差为 (3)相邻两暗纹间距\n(4)条15.10使自然光通过两个偏振化方向夹角为60°的偏振片时，透射光强为，今在这两个偏振片之间再插入一偏振片，它的偏振化方向与前两个偏振片均成30°，问此时透射光与之比为多少?解：由马吕斯定律∴15.12一束自然光从空气入射到折射率为1.40的液体表面上，其反射光是完全偏振光．试求：(1)入射角等于多少?(2)折射角为多少?解：(1)∴(2)15.14光由空气射入折射率为的玻璃．在题15.14图所示的各种情况中，用黑点和短线把反射光和折射光的振动方向表示出来，并标明是线偏振光还是部分偏振光．图中题图15.14解：见图．\n题解15.14图