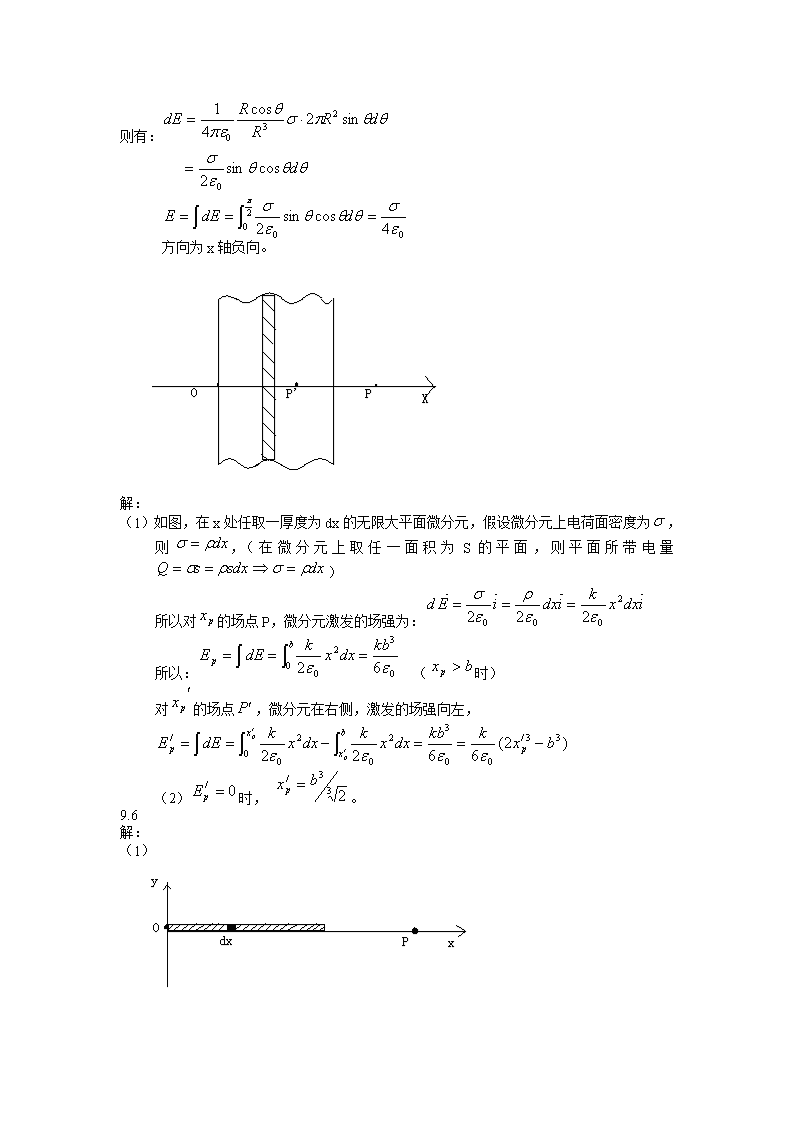大学物理下答案05227 31页

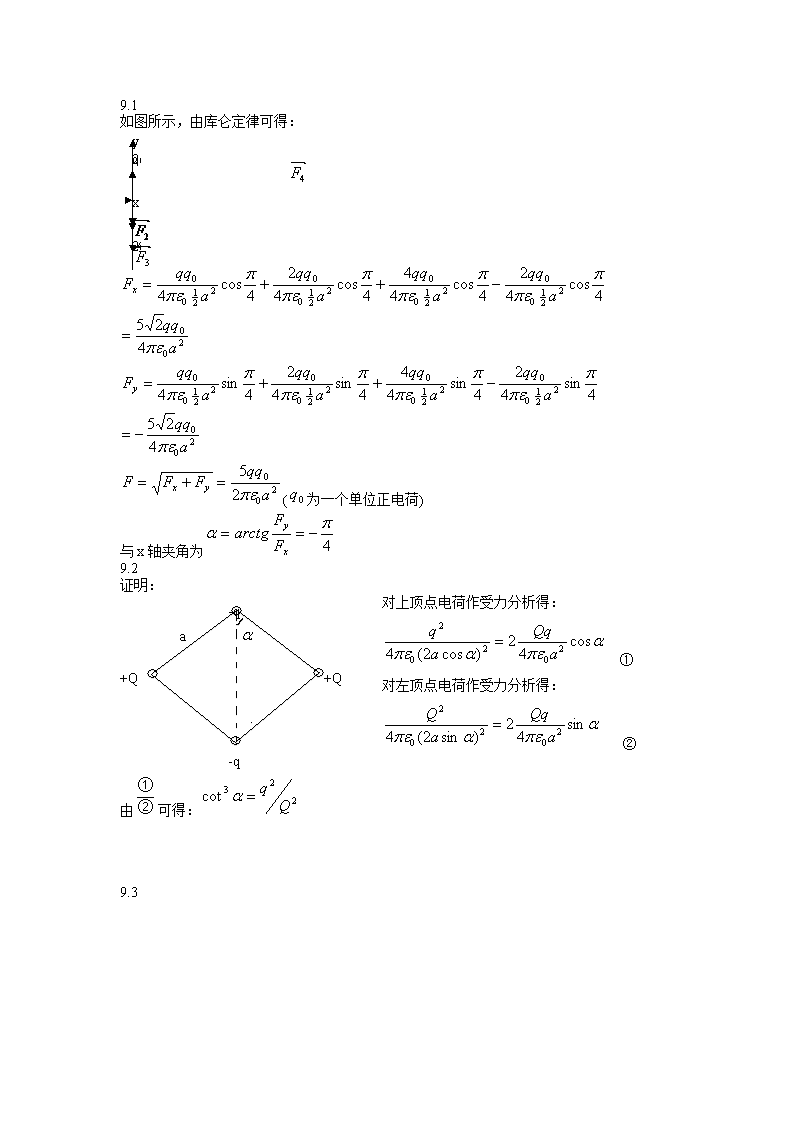
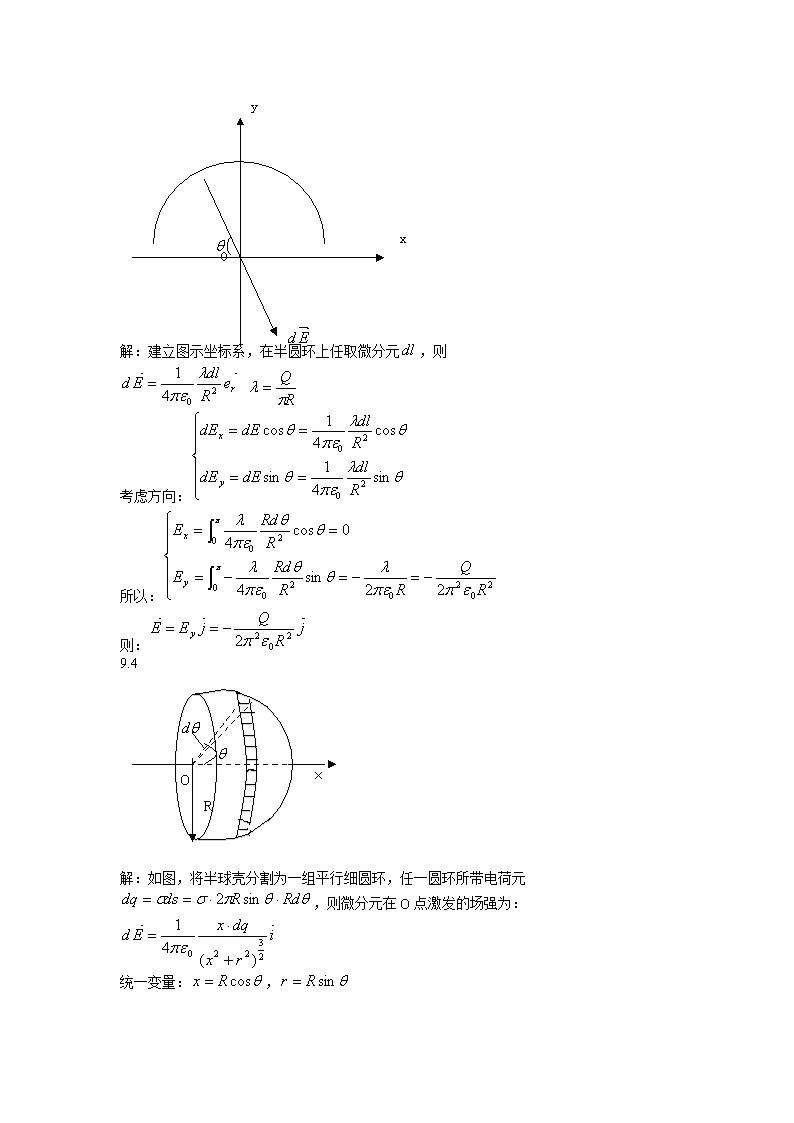
9.1如图所示，由库仑定律可得：xyq2q2q-4q(为一个单位正电荷)与x轴夹角为9.2对上顶点电荷作受力分析得：①对左顶点电荷作受力分析得：②证明：a+Q+Q-q由可得：9.3\n解：建立图示坐标系，在半圆环上任取微分元，则考虑方向：所以：则：9.4ｘRO解：如图，将半球壳分割为一组平行细圆环，任一圆环所带电荷元，则微分元在O点激发的场强为：统一变量：，\n则有：方向为x轴负向。解：（1）如图，在x处任取一厚度为dx的无限大平面微分元，假设微分元上电荷面密度为，则，（在微分元上取任一面积为S的平面，则平面所带电量）所以对的场点P，微分元激发的场强为：所以：（时）对的场点，微分元在右侧，激发的场强向左，（2）时，。9.6解：（1）\n取图示坐标系，在x处取微分元dx，则（2）由例9.3得所以9.7解：如果把半球面看成闭合的，由高斯定理有9.8解:\n如图，过场点作与球同心球面S，因电荷分布为球对称，则球电场分布也应为球对称，所以S面上各点电场强度的大小相等，由高斯定理，可得当时，当时，所以9.9解：r做半径为r，高为h的同轴闭合圆柱面，由高斯定理有：r9.10解：\n（1）如图，在环上取微分元，半径为r，宽为dr的带电细圆环，其所带电量为沿轴线建立坐标系OX，带电细圆环在轴线上产生的电势为则(2)根据能量守恒定律，可得OCD9.11解：＋q（1）（2）9.12O解：\n由高斯定理有时：或：当时，当时，9.13解：（1）如图所示，取微分元dx，则（2）9.14解：如图设坐标，上有电量，整个带电线受的电场力在球面电荷的电场中的电势能：整个带电线的电势能为：\n9.15解：（1）由叠加原理可得出结论，处场强可以看作是由体密度为，半径为R的球心在O点的均匀带电球与体密度为，半径为，球心在点的均匀带电球共同激发的，所以由高斯定理可得：对点，r＝0，所以E2＝0。则方向由O指向。（2）处电势（3）10.1\n解：其中两直线电流在O点产生的磁感应强度为0，1/4圆电流在O点产生的磁感应强度方向垂直纸面向里，大小为。ab⊙⊙cd10.2解:如图过中心平行于(如图竖直向上)。10.3⊙解:方向垂直纸面向里，大小为方向纸面向右，大小为方向在过垂直于的平面内与夹角10.4解：两线圈在P点产生的磁感应强度方向都在两圆心的连线上指向小圆（向左）10.5解：\n由对称性可知10.6解：对于无限大平面载流导体板，即上题结果中，（i为电流密度）（1）在两面之间产生的磁感强度大小为，方向垂直纸面向里。在两面之间产生的磁感强度大小为，方向垂直纸面向外。总的磁感强度B的大小为。（2）在两面之外的空间里，产生的磁感强度大小为。在两面之外的空间里，产生的磁感强度大小为。\n二者方向一致，总的磁感强度B的大小为（3）时，两板之间的磁感强度为两板之外的磁感强度为10.7解：旋转的带电圆盘可等效为一组同心圆电流，在盘面上割取细圆环，其等效圆电流为此圆电流在P点产生的磁感强度大小为，方向沿x轴。所以，P点上的磁感强度大小为方向沿0x轴。10.8解：ab（1）由安培环路定理知(2)得(3)由安培环路定理知，方向都是图中顺时针10.9解：(1)(2)10.10解：(1)由对称性可知环内的磁感应线是同心的逆时针方向的圆,在环内做半径为\n的圆作为闭合回路，绕行方向规定为逆时针，故(2)10.11解：当线圈转到此位置时，重力矩与线圈的安培力矩达到平衡，线圈所受的安培力矩为线圈所受的重力矩为（）10.12解：（1）向左滑时磁场力作正功，（2）向左滑时磁场力作负功，10.13解：10.14解：设线圈平面的法向与之间的夹角为，则线圈所受的安培力矩为线圈在平衡位置作微小摆动，很小，因此根据转动定律即简谐振动的角频率为则此摆动可看作简谐振动周期10.15解：（1）所受安培力矩大小为\n方向在纸面内垂直于向上(2)力矩所作的功10.16ABDOaC解：I方向向左10.17解：（1）（2）电子所受洛伦兹力为①经电压U加速后所具有的初速度为V，\n②电子以洛伦兹力为向心力在磁场中做圆周运动，③联立可得10.18解：设质子的质量为m，电荷为q；氘核的质量为2m，电荷为q；粒子的质量为4m，电荷为2q。（1）当三种粒子经相同电压加速后，质子所获动能氘核所获动能粒子所获动能则三者的动能比为1：1：2。（2）当它们经这样加速后进入同一磁场时（可利用上题结果）质子的运动半径氘核的运动半径粒子的运动半径则氘核与粒子的运动半径相等，均为14.1cm。10.19解：证：由离子源产生的离子在电势差为U的电场中加速，根据功能原理，有①离子以速度v进入磁场后，其动力学方程为②联立可得10.20解：上面负\n10.21解：（1）（2）相对磁导率为的磁介质外表面的磁化强度为相应的磁化电流为其方向沿z轴正向。相对相对磁导率为的磁介质内表面的磁化强度为相应的磁化电流为其方向沿z轴负向。其方向沿z轴负向。10.22解：由安培环路定理得铁心内磁场强度大小为10.23解：（1）（2）\n（3）磁化电流磁化电流密度10.24解：为图中曲线的最大斜率11.2解:bc部分产生电动势c端电势高。11.3解：DC在CD杆中取线元dl，距导线距离为x，如图，线元dx处的为（向外为正向）\nD端电势高。11.4(1)解：对线元段，电荷，旋转成圆形电流，则其在O点产生的磁场为（2）（3）若则方向为正，Bo方向垂直纸面向里，方向为垂直纸面向里11.6解：(1)取矩形面元积元\n（2）11.7解：设半圆形导线法向方向与方向相同时开始计时11.8解：11.9解：长直螺线管内部的磁场各部分均匀梯形面积方向沿11.10证明：大小为11.11证明：磁能密度\n由安培环路定理得证。11.12解：11.13解：11.14解：（1）（2）与I的变化方向相反。11.15解：（1）\n（2）大小11.16解：（1）设正六边形线圈中通电流I，正六边形线圈每条边在中心处产生的大小相等，方向相同，为中心处总的磁场强度为（2）11.17解：（1）球形电容器电容位移电流密度（2）\n11.18解：沿导线方向单位长度电阻为R，单位长度电量为Q在其附近产生的E大小电场能量密度（2）12.1解：由于12.2解：每个光子能量为，设每平方米每秒通过的光子数为N，则12.3解：12.4解：\n由于斜率是常数，不同金属斜率相同。12.5解：12.6解：12.7解：12.8解：光子能量光波为紫外光，应跃迁至第一能级。解出12.9解：最小轨道半径为12.10解：总能，所以要用相对论来讨论。\n12.11解：由德布洛意关系由布拉格公式二者符合。12.13解：要归一化，积分得的最大值处为发现粒子概率最大的地方，可知处为所求。12.14解：（1）由可得（2）12.17解：概率\n当时，；当时，趋向经典结果。12.18解：在无限深势阱中，，最小能级：精确解，可见二者具有相同的数量级。13.2证：13.4证：13.5解：\n13.6解：13.7解：（1）是，本征值（-1）（2）是，本征值（-1）（3）不是。13.8证：由两边用作用因为，对易可见也是的属于的本征函数，但由于并不简并，所以与\n属于同一量子态，只能差一常数即也是的本征函数。13.9证明：设的本征态为，则由于最后一步用到。13.10解：则，，角动量与z轴夹角设为，,得、、、、。13.11解：按归一化13.12解：\n即是第一和第三个能量本征态的叠加，所以测得能量本征态可为，概率为，概率为则13.13解：由于所以能量为的概率为所以能量为的概率为13.14解：即是的本征函数。13.15解：基态，，则波函数为径向概率密度为\n对上式求导使其为0即在距核玻尔半径处发现电子的概率最大。13.16解：13.17解：概率应为13.18解：由习题13.5得由习题13.6得\n所以13.19解：在原子中，设，上式对求导，使之为零，得得，代入与精确解同数量级。13.20证明：与互易，有共同本征函数，可用展开由薛定谔方程，所以两边积分得所以即测量A的概率分布不随时间变化。\n14.1解：①有，，共四种，本征值，，②有，共三种，本征值，，③共一种，本征值14.2解：电子组态是电子的四个量子数分别是14.3解：l＝1，则14.4解：无限深势阱，，\n所以，基态能量的一级修正同理第一激发态能量的一级修正为所以，基态能量为第一激发态能量为14.5解：设基态与第一激发态能级分别为和，原子数分别为和。，