大学物理(分子物理部分) 34页

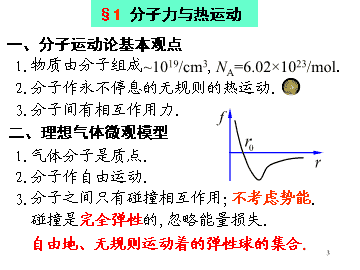
第三章气体分子运动论§2理想气体的压强公式和温度公式§3能量按自由度均分原理§4气体分子的麦克斯韦速率分布§5平均碰撞频率和平均自由程§1分子力与热运动研究气体宏观现象的微观本质.1\n*1.热学:研究自然界物质与冷热有关的性质,热运动的规律.*2.对象:大量分子组成的系统,理想气体分子.*3.内容:宏观量规律:系统属性.微观量规律:个别分子.内在联系:微观本质.*4.方法:气动理论:从微观结构出发,力学规律+统计平均→宏观规律.热力学:从宏观量出发,系统变化时P,V,T的变化,W,Q,ΔE转化关系.2\n§1分子力与热运动1.物质由分子组成~1019/cm3,NA=6.02×1023/mol.2.分子作永不停息的无规则的热运动.3.分子间有相互作用力.rf一、分子运动论基本观点碰撞是完全弹性的,忽略能量损失.二、理想气体微观模型2.分子作自由运动.1.气体分子是质点.3.分子之间只有碰撞相互作用;不考虑势能.自由地、无规则运动着的弹性球的集合.3\n1.平衡态:系统宏观性质和状态不随时间变化,微观状态千变万化的热动平衡.准平衡态:在变化过程中无限接近平衡态.3.状态方程:平衡态下热力学量之间的关系.三、理想气体的宏观描述2.状态参量:四、宏观量与微观量表征大量分子集体特性的量---宏观量.描述一个分子或原子的物理量---微观量.4\n一.宏观假设(平衡态)1.分子的空间分布是均匀的；2.分子的运动是各向同性的,等几率原理.§2理想气体的压强公式和温度公式二.理想气体的压强公式大量气体分子中的一个--统计平均--描述大量.认为压强是气体分子对器壁碰撞造成的,和雨伞受雨滴平均压强.不可能对一个分子研究.单分子碰撞,冲力,大量分子冲力,统计平均.5\nN个分子(同类),质量m与A1相撞一次单位时间碰撞A1次数:单位时间对A1总冲量:对N个分子求和,冲量定理长方形容器边长选一个分子6\n理想气体的压强是单位体积内气体分子平均平动动能的量度.单位时间内Δt=1还取决于n.一个气体分子平均平动动能.7\n玻耳兹曼常数三、温度公式理想气体温度与气体分子平均平动动能成正比.温度公式:方均根速率:8\n理想气体的绝对温度是大量气体分子平均平动动能的量度.也是大量分子热运动强度的量度.温度是大量分子热运动的集体表现,具有统计的意义,对一个分子讲是无意义的.若两种气体温度相同,则两种气体的分子平均平动动能相同.温度相同的n种气体混合贮于同一容器中,则混合气体的压强等于各气体分压强之和.即,则分子停止运动.错误.若T=0,由道而顿分压定律9\n例1:一定量的理想气体贮于一容器中,温度为T,气体分子质量为m.根据理想气体分子模型和统计假设,分子速度在x方向的分量的下列平均值0kT/m例2:下列式中哪一式表示气体分子的平均平动动能？(式中M为气体的质量,m为气体分子质量,N为气体分子总数目,n为气体分子数密度,NA为阿伏加得罗常量)()A10\n质点:平动:x,y,z3个刚体：质心x,y,z3个转轴a,b,γ转角φ二、气体分子的自由度单原子分子:3平动双原子分子:3平动+2转动+1振动(弹性键)§3能量按自由度均分原理一、自由度的概念决定物体空间位置的独立坐标数目.两个独立转动共3个co双原子分子:3平动+2转动(刚性键)11\n对于由n个原子构成的分子,自由度最多为3n,其中3个平动,3个转动,其余的是振动自由度.多原子分子:非共线三原子分子,3平动+3转动+3振动理想气体的自由度和温度有关,一般温度较低时振动自由度不出现.常温以下不考虑振动,双原子分子自由度为5.刚性双原子分子:3平动+2转动t平动自由度r转动自由度s振动自由度弹性双原子分子:3平动+2转动+1振动12\n三、能量按自由度均分原理推广:在温度为T的平衡状态下,分子的每个自由度具有相同的平均能量为kT/2.平均振动势能:总平均动能:理想气体分子平均能量：振动自由度占两份能量.能量按自由度均分原理是统计规律,单个分子不成立.平动有3个自由度13\n四、理想气体的内能理想气体内能可忽略分子间的势能.理想气体内能:理想气体内能变化与状态量T有关,与过程无关.气体分子具有平动、转动、振动动能和势能及分子之间相互作用势能,总和--内能.N个分子:定量的理想气体内能决定于分子的自由度和气体的绝对温度,与气体的体积和压强无关.弹性刚性14\n例3:在标准状态下体积比为1:2的氧气和氦气(均视为刚性分子理想气体)相混合,混合气体中氧气和氦气的内能之比为()A.1:2B.5:6C.5:3D.10:3B1.理解气体压强与温度的微观解释和方法.2.理解自由度和自由度均分原理,会计算理想气体的内能.本课要求：P160习题3、6、8作业:15\n探测器个别分子的速率是偶然的,大量分子速率分布是稳定的.速率范围：§4气体分子的麦克斯韦速率分布一、分子速率的实验测定16\n麦克斯韦速率分布函数大量分子:分布在速率v附近单位速率间隔内的分子数占总分子数的百分比.一个分子:分子速率在v附近单位速率间隔内的概率,概率密度.二、麦克斯韦速率分布vf(v)f(v)v+Dvvv017\n意义与用途:1.点:概率密度.2.小面积：3.总面积：4.极值：最概然速率:该速率分子出现概率密度最大.vf(v)T1T2>T1T高vp大,分布分散.v18\n平均速率：5.求分子速率的分布情况：6.求速率的各种平均值：连续分布方均根速率：19\n方均根速率:vf(v)平均速率:最概然速率:三、三个常用的分子速率统计值分子碰撞,迁移分子速率分布分子平均平动动能室温约300K,氧气太阳表面5800K,20\n例1:下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线？()BA.f(v)voB.f(v)voC.f(v)voD.f(v)voN2He21\n例2:说明下列各式的物理意义.平衡态下,处在速率间隔v~v+dv内的分子数占总分子数的百分比.平衡态下,处在速率间隔v~v+dv内的分子数.平衡态下,单位体积中处在速率间隔v~v+dv内的分子数.分子数密度.平衡态下,处在速率间隔v1~v2内的分子数占总分子数的百分比.22\n平衡态下,处在速率间隔v1~v2内的分子数.平衡态下,速率大于vp的分子数占总分子数的百分比.平衡态下,处在速率间隔0~∞内的分子数占总分子数的百分比.全部分子百分之百地分布在0~∞的整个速率范围内.速率分布函数的归一化条件.23\n平衡态下,大量分子热运动速率的算术平均值.分子的平均速率.平衡态下,大量分子热运动速率平方的平均值.分子的方均速率.平衡态下,处在速率间隔v1~v2内的分子对方均速率的贡献.注意:它与方均速率的区别.24\n平衡态下,全部分子的平动动能的平均值.平衡态下,分子速率在v1~v2内分子的总平动动能.平衡态下,速率处在v1~v2间的分子的平均速率.2.观察被积函数的物理意义及积分区间.3.注意这是一个对大量分子的统计规律.1.明确速率分布函数的物理意义.25\n例3:有N个假想的气体分子,其速率分布如图示,当v>2v0时,f(v)=0,求(1)常数a;(2)速率大于v0的分子数;(3)分子的平均速率.Nf(v)vv02v0a0解:(1)速率分布函数必须满足归一化条件,即26\n27\n碰撞截面平均碰撞频率:单位时间内分子与其它分子平均碰撞次数.平均自由程:两次碰撞间自由飞行的平均路程.§5平均碰撞频率和平均自由程凡中心在这管内均碰撞,当其他分子不动时,单位时间内分子与其它分子平均碰撞次数：2d2dd钢球模型:忽略分子的结构,直径为d.28\n考虑其他分子也运动,相对运动常温常压下，T、P代入得平均自由程：一般n不易得到，用宏观量表示:平均碰撞频率：29\n例4:某种气体分子的平均自由程为5×10－4cm,方均根速率为500m/s,求分子的碰撞频率.解：30\n一定量的理想气体,在容积不变的情况下,不随温度T变化,而与成正比;在压强不变的情况下,与温度T成正比,而与成反比.31\nB例5:容积恒定的容器内盛有一定量的某种理想气体,其分子热运动的平均自由程为,平均碰撞频率为,若气体的热力学温度降低为原来的1/4倍,则此时分子平均自由程和平均碰撞频率分别为()32\n1.分子运动图景2.宏观量3.微观量4.关系本章小结：5.33\n1.理解气体分子的麦克斯韦速率分布律的表达式及物理含义,会应用.3.理解和会算平均碰撞频率和平均自由程.2.理解和会算三个特征速度.4.了解大量分子的研究方法.本课要求：P160习题11、12、15作业:34