大学物理——机械波 21页

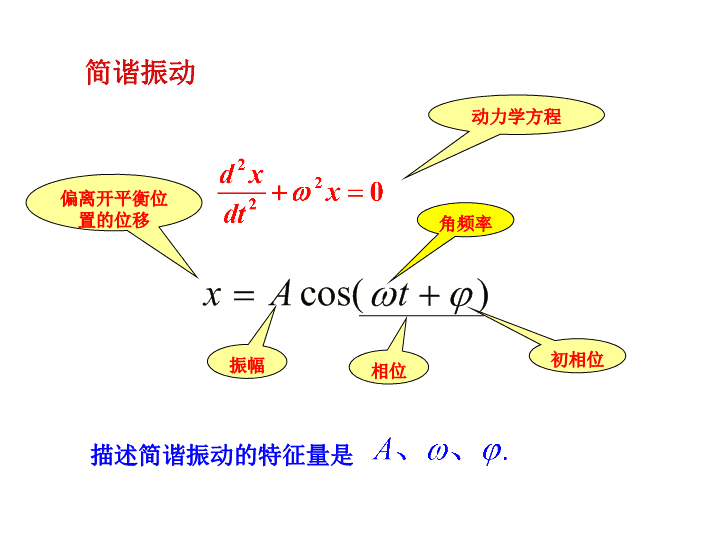
简谐振动动力学方程振幅相位初相位描述简谐振动的特征量是角频率偏离开平衡位置的位移\n第15章机械波引言：波振动的传播过程称为波动，简称为波。本章以机械波为例讨论波动过程的特征和规律。虽然各种波产生的本质有所不同，但它们都具有一些共同的特征和规律，例如具有一定的传播速度，能产生反射、折射、干涉、衍射等。机械振动的传播过程称为机械波。电磁振动的传播过程称为电磁波（光波）。另外任何物体都具有波动性，当研究范围进入微观领域（原子限度）时，粒子的波动性明显显现出来，这种波动性称为物质波。\n15.1.1机械波产生的条件：§15.1机械波的产生及特性弹性介质：介质元连续分布，介质元之间有弹性相互作用。15.1.2波的分类1、按振动的物理量,可分为机械波、电磁波等。2、按传播方向和振动方向的关系,可分为横波和纵波等(1)横波:振动方向与传播方向垂直。(1)要有振动(波源)；(2)要有能传播振动的弹性介质。(2)纵波:振动方向与传播方向平行。例：绳上波；电磁波（光波）。例：空气中声波。另外地震波既有横波又有纵波，是横波和纵波的叠加。\n15.1.3波的特征量1、波的传播速度u：单位时间内波（振动状态或相位)传播的距离，称为波的传播速度，简称波速或相速，用u表示。t=00481620············12······································t=T/2······························t=T·············································t=3T/4t=T/4\n所以说波动是振动状态的传播，是相位的传播，是能量的传播，而不是质点的传播。波的传播速度与介质有关，不同的介质内波的传播速度不同。例：室温下，频率ν=200Hz的声波在空气中u=340m/s,λ=1.7m;在水中u=1450m/s,λ=7.25m。2、波长λ:完成一个全振动所传播的距离。或者说波传播过程中,沿波传播方向上两个相邻的同相位（相位差为2π）的两介质元间的距离。反映了波在空间上的周期性。就是在相同的介质内由于介质的特性，横波和纵波的传播速度也不相同。\n3、波的周期T：波传播一个波长所需要的时间。反映了波在时间上的周期性，当波源与观察着相对静止时，波的周期与波源的振动周期相同。4、频率ν：周期的倒数；单位时间传播完整波的数目。波速u与波长λ、周期T(频率ν)的关系\n机械波的波速u1、固体中的波速横波:纵波:式中:G——切变弹性模量Y——杨氏弹性模量ρ──质量密度因为波的传播速度u与介质的性质有关，不同的介质内，波的传播速度不同，所以u的大小决定于介质的性质。横波:只能在固体中传播。纵波:在固体、液体、气体中都能传播。(1)切变弹性模量GflS△r切应变：切应力：实验表明：切应力与切应变成正比即左端固定θ切向力或剪切力写成等式：\n（2）杨氏模量Ylsf△l应变应力实验表明：应力与应变成正比由于固体的杨氏模量Y总是大于切变弹性模量G，所以纵波波速总是大于横波波速。2、液体、气体中的波速(仅有纵波)B——液体或气体的容变弹性模量ρ——媒质的密度写成等式：\n结论：波速取决于介质的性质。3、张紧的弦上传播的横波的波速T──弦中张力μ──单位长度上的质量1、波阵面（波面）:某时刻相位相同的点组成的空间曲面；15.1.4波的几何描述——波面、波线、波前波面波线波线波面2、波前:某时刻在最前面的波阵面；3、波射线（波线）:沿波的传播方向作的射线；在各向同性均匀介质中，波线与波阵面垂直。波前波前为了形象地描述波的传播过程中，各振动质点之间在相位上的关系，引入波阵面和波射线等概念。例球面波平面波\n§15.2平面简谐波的波函数描述波在传播过程中，不同位置x处的质点偏移平衡位置的位移y与时间t的函数关系。波函数:简谐波（余弦波）：15.2.1平面简谐波的波函数1、平面简谐波：简谐波的波阵面为平面的波。分析：根据波面的定义任一时刻波面上各质点的振动状态相同，相位相同，离开各自平衡位置的位移也相同，所以只要研究波线上各点的波动规律即可知整个平面波的波动规律。是简谐振动所形成的波，是简谐振动的传播过程。波线波面\nxyo点处质点的振动方程为y为t时刻,o点(x=0点处)振动质点离开平衡位置的位移在波线上任意取一点p，坐标为x。o点的振动传播到p点所用时间为。那么p点在t时刻的振动状态与o点在时刻的振动状态相同。平面简谐波的波函数（t-τ）设：一平面余弦波沿x轴正方向传播，波速为u。记\n∴上式又可表示成若平面余弦波沿x轴负方向传播时，p点的振动将与o点在时刻的振动状态相同。平面简谐波的波函数（t+τ）记\n∴沿x轴负向传播的平面简谐波的波函数为比较振动方程和平面简谐波的波函数各代表的物理含义：描述波源或者x=0处质点的位移随时间t的变化规律描述波线上所有质点在t时刻离开平衡位置的位移描述x处质点的位移随时间t的变化规律；即x处质点的振动方程。记\n(2)当t=t0给定,则有:说明y=y(x),表示t0时刻各点离开平衡位置的距离。注意:波形图(y-x)与振动曲线(y-t)的区别。15.2.2波函数的物理意义(1)当x=x0给定时,则有:表示x0处质点的振动规律(振动方程)。x0点的振动曲线t0时刻的波形曲线(3)当x、t都变化时,y=y(x,t)表示不同时刻,不同位置处各质点位移。yotxyt=t0\n波函数全面反映了波在时间上和空间上的周期性。(4)由波函数可求得各质点的振动速度、加速度注意：v和u的不同。t1时刻的波形图t1+△t时刻的波形图xyo传播的距离\n15.2.3波动方程（动力学方程）平面简谐波满足的方程（1）（2）（2）/（1）得平面波的波动方程推广到其它物理量，只要它的运动规律满足该式，就表示它是以u为传播速度的平面简谐波。例：电磁波在真空中传播满足的波动方程说明在真空中传播的电磁波是以c为传播速度的平面简谐波.\n例15-1设有一沿x轴正方向传播的波，波长λ=0.1m,p点处质点的振动方程为y=0.03cosπt（m）,试求下列两种情况下的波函数。（1）p点位于坐标原点；（2）p点位于x0=0.2m处。解:（1）设简谐振动方程为则波函数为根据题意，p点位于坐标原点时，其振动方程为ox\n（2）当p点位于x0=0.2m时，ox0x所以波函数为传播到任意点x处所用时间为要点:抓住沿波的传播方向上各点相位依次落后。p点的振动方程为u\n例15-2一平面余弦横波沿水平张紧的绳上自左向右传播。取绳的左端为坐标原点，x轴的正方向水平向右,y轴的正方向竖直向上。t=0时，绳的左端经平衡为止向下运动。振幅A=0.1m,频率ν=0.5Hz,波速u=1ms-1。求波函数和距原点1.5m处质点的振动方程。解：∵ν=0.5Hz,∴T=2s,ω=πrads-1设原点o处的振动方程为根据题意:t=0时，y=0。即得又∵t=0时，质点向下运动，v<0.则波函数为\n把x=1.5m代入上式，得1.5m处的振动方程为例15-3波源的振动曲线如图所示。已知波速u=4cms-1,方向向右，求t=3s时的波形曲线。解：12345t/sy/cm0.5-0.5由图可知A=0.5cm,T=4s,设波源的振动方程为t=0时，y=0.5cm即∴波函数为\n波函数t=0s时的波形图t=3s时的波形图当t=3s时，波向前传播的距离为△x=ut=12cm∴将图像向前平移△x=12cm的距离得，t=3s时的波形图。481216x/cmy/cm将t=0s代入上式，通过描点画图得t=0时的波形图。12cm或将t=3s代入上式，通过描点画图得t=3时的波形图。结束