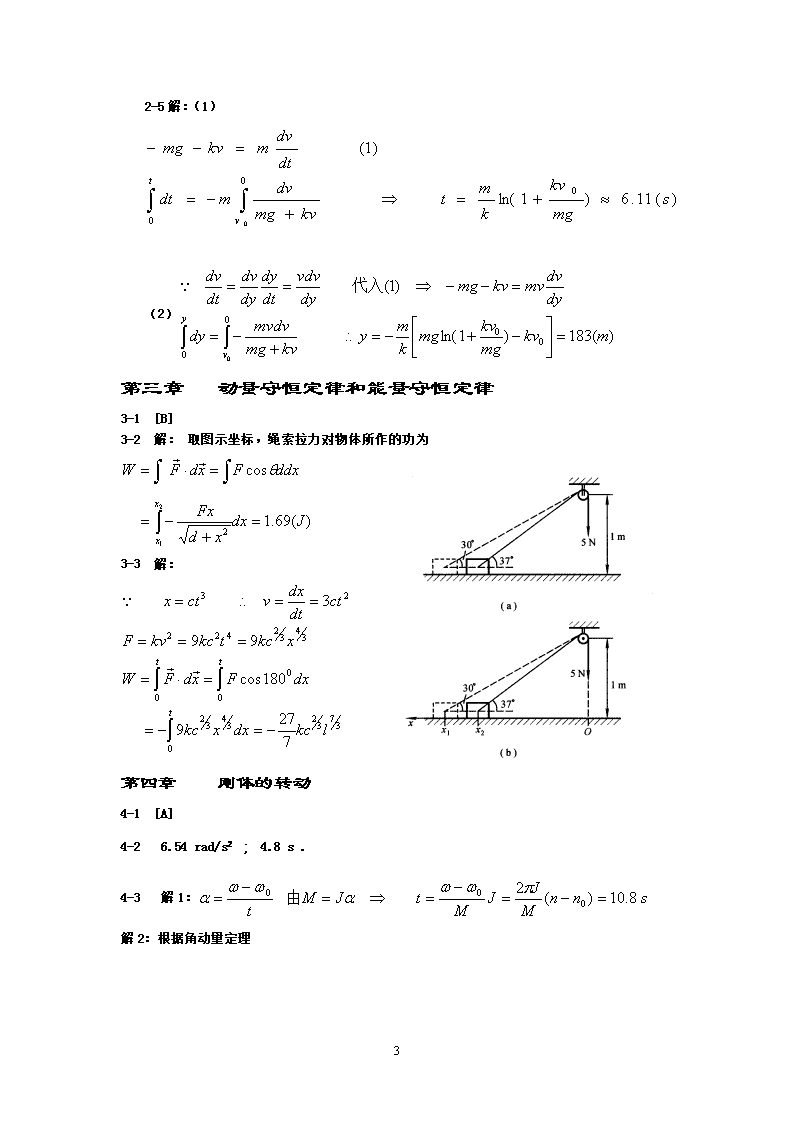大学物理课后答案 40页

大学物理习题答案第一章质点运动学1-1D。1-223m/s1-3解：x/my/mO10m1-4解：由加速度4解：由加速度定义，及初始条件，积分得1-5解：(1)取如图所示的坐标，物品下落时在水平和竖直方向的运动方程分别为(2)视线和水平线的夹角为（3）在任意时刻物品的速度与水平轴夹角为取自然坐标，物品在抛出2S时，重力加速度的切向分量与法向分量分别为40\n第一章牛顿定律2-1140N/S；24M/S。2-2解：取沿斜面为坐标轴OX，原点O位于斜面顶点，则由牛顿第二定律有（1）又物体在斜面上作匀变速直线运动，故有为使下滑的时间最短，可令dt/da=0,由式（2）有2-3解：因加速度a=dv/dt,在直线运动中，根据牛顿定律有120t+40=mdv/dt根据初始条件，积分得2-4解：以地面飞机滑行方向为坐标正方向，由牛顿定律及初始条件，有40\n2-5解：（1）（2）第一章动量守恒定律和能量守恒定律3-1[B]3-2解：取图示坐标，绳索拉力对物体所作的功为3-3解：第二章刚体的转动4-1[A]4-26.54rad/s2;4.8s.4-3解1：解2：根据角动量定理40\n4-4[C]4-5解：4-6解：根据角动量守恒定律4-7解：小孩与转台作为一转动系统，系统的角动量守恒。设人和转台相对地面的角速度分别为而人相对转台的角速度应满足根据角动量守恒定律分别为转台，人对转台中心轴的转动惯量。所以转台的角速度为负号表示转台转动的方向与人对地面的转动方向相反。4-8解：（1）由刚体的角动量定理得（1）（2）取棒和地球为一系统，并选O为重力势能零点。在转动过程中，系统的机械能守恒。即40\n4-9解：（1）棒绕端点的转动惯量为，由转动定律，得棒在任意位置时的角加速度为AOP当（2）机械能守恒，棒下落至竖直位置时的动能为（3）棒下落至竖直位置时的角速度为第一章热力学基础p/(1.0×105Pa)21123V/(1.0×10-3m3)OABCD6-1[B]6-2[A]6-3解：功的数值等于P-V图中过程曲线下的面积6-4解：根据初始条件得氧气的物质的量为。已知氧气的定压、定体摩尔热容分别为（1）40\n（2）6-5解：系统经ABC过程所吸收的热量及对外所作的功分别为则由热力学第一定律可得由A到C过程中系统内能的增量为6-6解：(1)a-b等容过程中气体不作功，内能增量为在b-c等温过程中内能不变，体积从V0增加到场2V0，氢气对外作功为在abc过程中氢气吸收的热量为（2）在a-d等温过程中内能不变，氢气对外作功为在d-c等容吸热过程中气体不作功，内能增量为在adc过程中氢气吸收的热量为6-7解：因AB、CD为等温过程，循环过程中系统作的净功为由于吸热过程仅在AB和DA段，所以，循环过程中系统吸热的总量为40\n6-88证明：（1）对AB、CD、BC、DA分别列出过程方程：联立求解上述各式，可证得（2）虽然该循环效率的表达式与卡诺循环相似，但并不是卡诺循环。其原因是：1、卡诺循环是由两条绝热线和两条等温线构成，而此循环却不是；2、式中T1、T2的含意不同，本题中T1、T2只是温度变化中两特定点的温度，不是两等温热源的恒定温度。6-9解：热机必须工作在最高的循环效率时，才能获取最大的功率。由卡诺定理知，可逆卡诺热机的效率最高。已知热机在确定的时间内吸取的热量，故由效率与功率的关系式，可得最大。功率6-10解：全过程的熵变是三个分过程的熵变之和，即：-100C冰——00C冰——00C水——100C水。1、3两过程可视为等压过程，则两过程的熵变分别为40\n过程2是等温熔化过程，吸热为Q=mL，该过程的熵变为：6-11解：（1）ADB过程的熵变为：（2）ACB过程的熵变为：通过计算看出，虽然过程不同，但熵变相同。第七章气体动理论7-1[B]7-2（1）1摩尔气体的内能。（2）定容摩尔热容。（3）定压摩尔热容。7-3解：（1）单位体积分子数：（2）氧气的密度：（3）氧气分子的平均平动动能：（4）氧气分子的平均距离：40\n7-4[D]7-5（1）速率大于最概然速率的分子数占总分子数的比率。（2）理想气体分子的平均平动动能。7-6（1）曲线1表示O2气分子的速率分部曲线；曲线2表示He气分子的速率分部曲线。（2）表示氧气分子数所占比率。（3）表示全体分子所占比率为1。7-7解：氢气分子的最概然速率为7-8解：（1）由于分子所允许的速率在0——2V0的范围内，由归一化条件可知图中曲线下的面积为系统分子总数N(3)速率在v0/2到3v0/2间隔内的分子数为（4）分子速率平方的平均值为第8章8-1C40\n8-2D8-3解：夸克视为经典点电荷，由库仑定律(N)＞0排斥力。8-4解：设其中一个点电荷带电q，则另一个点电荷带电，则两点电荷之间库仑力由极值条件，∴又＜0，则两电荷平分电荷Q时，它们之间相互作用力最大。8-5解：⑴建立如图坐标系。在细棒上距中点Ox处取线元dx，带电dqdxdq在P点产生d⑵P点在棒的中垂线上，由对称性分析：∴当棒长L→∞时，设棒单位长度带电荷为常量，则P点40\n()8-6解：在环上取线元dl，其带电，dq在O点产生由于圆环关于y轴呈对称性，则则，沿y轴负向。8-7解：将半球壳分割成一组平行细圆环，任一圆环带电量dq=dS=d=ddq在O点激发所有平行细圆环在O点激发的方向相同，且，∴∴方向沿x轴。8-8解：在x处取宽为dx细窄条，窄条单位长度带电量为dx，由无限长带电直线的场强公式可得窄条dx在P点产生场强为方向沿x轴正向。整个带电平面在P点产生，方向沿x轴正向。8-9D8-10解：根据高斯定理∴40\n8-11A8-12D8-13解：因电荷分布和电场分布具有球对性：球面上各点的大小为常量。由高斯定理可求得0≤r≤R∴r＞R∴8-14解：由于电荷分布具有轴对性，则分布具有轴对称性：同轴柱面上各点大小相等，方向沿垂直轴的径向，以OP=r为半径作同轴直圆柱面，高l为高斯面，由高斯定理可得：r＜R∴r＞R∴8-15证：用补偿法，问题等效为一个完整的、电荷体密度为的均匀带球和一体密度为、球心在的带电小球（半径为空腔球形的半径）。由高斯定理可求实心球内任一点P的场强为：∴，则腔内任一点P处8-16解：问题具有球对称性，取OP=r为半径的同心球面为高斯面。由高斯定理可有：r＜R1∴E1=0R1＜r＜R2∴40\nR2＜r＜R3∴r＞R3∴在带电球面两侧，左右极限不同，不连续。r=R3球面两侧，发生跃变，8-17C8-18400V8-19B8-20注：习题中应改为：解：[方法1]由题意，Q1所受的合力为零，解得由点电荷电场叠加，Q1、Q3在y轴上任一点将Q2从点O沿y轴移到无穷远处外力作功[方法2]由方法1知，在任一点电荷所受合力为零时，由电势叠加可得Q1、Q3在O点的电势为将Q2从点O移到无穷远过程中，外力作功8-21解：⑴在环上取半径为r，宽为dr的带电细圆环，其带电量dqdSdr，dq在轴线上任意点P处产生电势为dVx=0处，40\n⑵根据能量守恒定律，当质子从无穷远处射向圆环中心时，电势能逐渐增加，而质子动能随之减少，质子要穿过圆心，Ek≥0，设质子的速度为v0≥0≥即质子初速率不能小于。8-22解：电荷、场强分布具有球对称性，以OP=r为半径作同心球面为高斯面，由高斯定理可得：R1＜r＜R2r＞R2r＜R18-23解：由高斯定理可求场强分布：40\n取棒表面为零电势r≤Rr＞R8-24解：由高斯定理可求8-25⑴普遍适用⑵普遍适用⑶均匀电场8-26D8-27解：力矩力矩作功8-28解：利用均匀带电圆环在其轴线上任一点电势结果，在圆盘上取同心圆环（半径为r，宽度为dr）微元，带电dqdr，dq在轴线上产生⑴轴线上任一点P点⑵P点第九章9-1解：根据无限大均匀带电平面的场强公式，指向，方向为x轴正向。⑴A板上的电荷在P点产生场强40\n⑵同理B板上电荷在P点产生的场强⑶由场强叠加原理⑷B板拿走，A板表面电荷将在两侧表面均匀分布，设面密度为9-2B9-3解：设内球带电，根据静电平衡时电荷分布，可知分布具有球对称性，由高斯定理可求分布：r＜R1R1＜r＜R2r＞R2电势分布：r＜R1R1＜r＜R2r＞R2∵∴代入、V结果。∴r＜R1V1=V0R1＜r＜R240\nr＞R29-4B9-5解：电场分布具有球对称性：同心球面上各点大小相等，方向沿矢径方向。以OP=r为半径作同心球面为高斯面。由高斯定理有r＜R1R1＜r＜R2r＞R29-6解：设内圆柱沿轴线单位长度上带电量为，设R1＜r＜R2处任一点P，由高斯定理可求R1＜r＜R2柱内、外表面间电势差①内柱与柱内任一点P处的电势差②②÷①得：9-7解：⑴查表知二氧化钛的相对电容率173，则充满此介质的平板电容器的电容40\n(F)⑵(C)极板上自由电荷面密度(C•m)晶板表面极化电荷面密度(C•m)⑶(V•m)9-8解：设内球壳带电Q，则由高斯定理可求R1＜r＜R2⑴⑵9-9⑴正确。⑵介质内场强与原来一样。⑶电场能量增大为原来的倍。9-10解：导体极板A、B和待测物构成一有介质的平板电容器。则介质厚度若待测材料为金属导体，其等效电容导体材料厚度实地测量A、B间电容量C，根据上式可测出材料厚度。9-11解：⑴极板间电场为均匀场，则电场的能量密度40\n在外力作用下极板间距被拉开到2d，电场占有的体积V增到2V，电场能增量⑵两导体板带等量异号电荷，外力将其缓慢拉开时，有则外力作功外力克服静电引力作功等于静电场能量的增量。9-12解：设介质内、外场强分别为E、E0，且⑴则⑵作一直圆柱形高斯面，如图。由可得：⑶极板和间隙内场强⑷9-13解：设导线和圆筒的半径分别为R1和R2，沿轴线单位长度上所带电量分别为，由高斯定理，可求（R1＜r＜R2）间任一点场强，导线表面处（r=R1）场强最大。当表面处场强等于空气的介电强度EM时，对应导线和圆筒所带的最大电量①电容所能承受最大电压②将①代入②得40\n(V)9-14C9-15C第10章10-1解：电流密度j对中心轴对称分布，根据稳恒电流连续性，以O为原心，r为半径的同轴柱面上电流I相等。r=6.0mm圆柱面上(A/m2)10-2解：设内、外球壳分别带电±Q，两球壳间的电势差两球壳间电流10-3C10-4D10-5解：电极的接地电阻是指当电流经电极入地流至无穷远大地的电阻。（实际上远处有另一电极，但确定电极的接地电阻，主要取决于电极近处的大地电阻）。大地中离电极中心r处厚dr一层半球壳的元电阻为dR接地电阻10-6解：⑴(V/m)⑵(m/s)40\n第11章11-1解：距离无限长载流导线r处、方向可由右手定则判定，如图。M点N点(T)方向沿水平向左。11-2解：⑴其延长线过P点的电流对P点的磁场无贡献。方向⑵(T)11-3解：(a)方向⊙(b)方向(c)方向⊙11-4C11-5解：建立如图坐标系。⑴在细杆上取线元dx，带电dqdx，dIdqdx（半径为x圆电流）⑵a＞＞b方向⊙40\n11-6解：将半圆柱面分割成宽度的细电流，细电流与轴线平行，长直细线载有电流，dI在轴线上任一点激发d的大小，方向在Oxy平面，与dl引向点O的半径垂直，由对称性可知，方向指向Ox轴负向。11-7解：将半球面分割为无数薄圆盘片，每一圆盘片等效为一圆电流，任一圆盘片中电流为，dI圆电流在球O点激发。O点①其中，代入①∴，方向由电流I方向，用右手定则判定。11-80，1：211-9解：由磁场中高斯定理穿过半球面的磁感应线全部穿过圆面S，∴11-10解：同轴电缆导体内的电流均匀分布，则分布具有轴对称性。在垂直轴线的平面内，以平面与轴线交点O为圆心，OP=r为半径的同心圆上各点大小相等，方向沿各点切向，以此圆为安培环路，由安培环路定理有40\n11-11解：分布具有轴对称性，由安培环路定理可求Br＜R时，r＞R时，11-12解：⑴因分布具有轴对称性，则由安培环路定理可求R1＜r＜R2⑵设图中阴影面法线方向垂直纸面向外为正，在阴影中取面元dS=Ldr，如图，r为dS到轴线垂直距离。11-13证：⑴由对称性可知，在环内与环共轴的圆周上的大小处处相等，方向沿圆周的切线，在环内取半径为r的同心圆为安培环路。由安培环路定理有⑵取面元hdr=dS，通过dS的磁通量11-14解：由对称性分析可知，无限大平面两侧距平面等远点的大小相等且方向相反，它们均平行于平面且与电流方向垂直。取如图所示矩形和沿abcd环绕方向，ab∥cd∥，ad⊥，bc⊥，ab=cd=L，O、为ad、bc的中点，由安培环路定理有40\n，、与积分路径正交，方向由右手螺旋关系定。11-15C11-16D11-17解：回路两宽边b受力之和为0。两长边受力分别为垂直长边指向导线；垂直长边背离导线。(N)方向垂直长边指向长直导线。11-18正、负；11-19A11-20解：⑴(N•m)方向竖直向上。⑵(J)11-21证：由得又由得40\n11-22解：将导线分成两段直导线和一半圆弧三部分，在导线上任取电流元，由对称性知，半圆弧受安培力，其中，两段直导线部分所受安培力，若导线形状不变，，∴整个导线受安培力第12章12-1C12-2解：⑴电流分布具有轴对称性，取在与轴线垂直平面上，以轴线与平面交点O为圆心，以OP=r为半径作同心圆为安培环路（P为场点）。由安培环路定理有⑵磁化电流分布，抗磁质＜1，R1＜r＜R2，r=R1—IS与导体电流方向相反。r=R2—IS与外导体电流方向相反。12-3解：如图，选闭合回路C，由安培环路定理得铁心内40\n12-4解：⑴(或)具有轴对称分布，以OP=r为半径作同轴圆为安培环路，由安培环路定理有：r＜R1，，R1＜r＜R2，r＞R2，⑵根据r=R1r=R2第13章13-1解：i产生（距直导线r处的B）⑴⑵13-2⑴顺时针。⑵顺时针。13-3解：设导线在如图所示时刻为t=0，顺时针方向为回路正向，此时半圆形导线表面法线与间夹角为。经历t时刻，则任意时刻穿过回路的磁通量为由法拉弟电磁感应定律，有40\n回路中感应电流则感应电流最大为13-4解：建立如图所示坐标系，在导线上任取线元根据13-5解：通过abcd等腰梯形回路的磁通(V)方向顺时针。13-6解：设的正向如图所示。ac段产生感应电动势，(V)方向从a→c，c点电位高。(V)13-7解：建立如图所示坐标系，距O点x处取线元dx=dl(V)方向由B指向A，A点为高电势。13-8解：如图所示，分别在r＜R和r＞R两个区域内任取一电力线为闭合回路l（半径为r的圆），并设顺时针方向为回路正向。⑴r＜R40\nr＞R＞0，则电场线的绕向为逆时针。⑵r＞R(V•m-1)13-9证：由13-8题可知，在r＜R区域，感生电场强度的大小，设PQ上线元dx处方向如图，则金属杆PQ上13-10解：距导线x处穿过回路的磁通量(V)13-11解：其中方向e→f方向h→g40\n＞方向为efgh13-12解：由13-8题知：13-13解：由安培环路定理可求导线内任一点单位长度导线内贮藏磁能13-14解：设有电流I通过线圈，线圈回路是长方形，如图。由安培环路定理可求R1＜r＜R2穿过线圈自身回路的磁链为13-15解：⑴长直螺线管的自感为(H)⑵当(A•s-1)时，线圈中自感电动势为V13-16(a)设在直导线中载流I1，则通过线圈中的磁链40\n∴互感(H)(b)13-17C13-18解：⑴设螺绕环中电流为I，它在环内的磁感应线都是同心圆，以OP=r为半径作同心圆，圆为安培环路。由安培环路定理有⑵(H)13-19解：，当时，有(V•m-1)13-2013-21D13-22B13-231．感生电场。2．位移电流。13-24变化的电场激发涡旋磁场。13-25都是电场，都对置于其中的电荷有电场力的作用。13-26都按相同的方式激发磁场。第十四章40\nPPxxO14-1C14-2证明：选货轮受重力浮力平衡时质心处为坐标原点，x轴正向向下，由(a)图，平衡时浮力大小当质心位于(b)图中的x处时，货轮所受浮力(a)(b)货轮所受合力由于=常数，∴货轮在其平衡位置上下作的微小振动为谐振动。由牛顿第二定律得∴—周期。14-3解：振动系统的角频率为=40s—1在子弹射入木块的过程中，子弹和木块组成的系统水平方向不受外力，动量守恒。设振动的初速度即子弹和木块的共同运动初速度为v0，则：Ox=1.0m•s—1又因初始位移，则振动系统的振幅为=2.5×10—2m由于t=0时，且v0＜0，所以由旋转矢量图可得初相。谐振动方程为(m)14-4解：s—1Ox40\n⑴mOx⑵mOx⑶m14-5C14-6C14-7COx14-8解：由题意知A=0.06m，s—1t=0时，，v0＞0由初始条件可做旋转矢量图，得，则振动方程为m当t=0.5s时，质点的位移m=0.052m质点的速度m•s—1=0.094m•s—1m•s—20.513m•s—2Ox⑵由旋转矢量图可知转过的角度为设该过程所用时间为，则得s=0.833s14-9x=Acos（2πt/T-π/2）x=Acos（2πt/T+π/2）x=Acos（2πt/T+π）14-10解：⑴如图，选平衡位置处为坐标原点，则0.01m，0.01m，40\nxOl0自平由牛顿第二定律可得平衡时∴，其运动方程为谐振动方程的标准形式。∴该振动为谐振动。其中。⑵0.01m31.3rad/s4.98Hz⑶t=0时，∴，(m)。14-11D第十五章15-1Oyy015-2解：⑴由旋转矢量法得(m)⑵(m)⑶m15-3解：已知A点的振动方程为(m)40\nCBADxu9m8m5m⑴以A点为坐标原点(m)⑵以B点为坐标原点B点的振动方程为(m)波动方程为(m)⑶由⑴中的波函数C点的振动方程为(m)D点的振动方程为(m)⑷1.02.0x/my/mu0-0.50.5t=2s即C点比D点在振动相位上落后。15-4解：由所给波形图可知mms—1y/mx/m0t=0s为求原点的运动方程，可由时的波形图得如上图，得m将上图波形左移1m，得时波形。yO得时，，＜0由旋转矢量图知。t/s00.200.405.0uy/m所求运动方程为(m)。15-5解：由所示x=1.0m处质点的振动曲线如图，知时，，＞0∴而由旋转矢量法可知至s该矢量需转过，Oy/mt=5st=0转用时s，而∴s40\n∴ss—1∴波动方程为(m)而∴m•s—1x/my/mP1.000.05010.0m∴波动方程为(m)15-6C15-715-8解：由时的波形图可知m，m。P点向上运动知向左。∴v0＜0，而m•s—1⑴(m)⑵将m代入波动方程，得(m)时该点的振动速度为(m•s—1)=40.6(m•s—1)15-9解：=2.94m∴即B处传的波比A处传的波到P点在相位上超前。15-10解：⑴两列波在R处的相位差为⑵合振幅为40\n15-11振动方向相同，频率相同，S2的相位比S1的相位超前。15-12解：以AB两点的中点O为原点，取坐标如图。x⑴位于A点左侧部分AOPB而，为加强条件。∴A点左侧无干涉静止点。⑵位于B点右侧部分干涉相加强，无干涉静止点。⑶在AB之间的任一点P距原点为x处(m)干涉静止点应满足∴(m)共15个点为干涉静止点。15-13D15-14B15-15A15-16100m•s—140\n第十七章17-1变小，变小17-2A17-3上17-4解：薄片厚度n1n2n3d17-5解：nmnmnmnm只有nm在可见光范围。∴薄膜正面呈黄色。17-6解：⑴nmnmnmnm只有nm为可见光。∴正面呈红色。⑵反射光在正面增强则在透射时为减弱。∴nm40\nnm（不可见）nm（可见）nm（不可见）∴nm的光透射减弱。n1=1n2dn1=117-7解：μmnmnmnmnm即波长为600nm和428.6nm的反射光最大限度的增强。17-8B17-9C17-1017-1117-12BlΔl17-13解：热膨胀系数*m℃℃℃代入*式得K—117-14417-1540\n17-16解：干涉暗环半径即将nm，m，m代入，得nm17-17B17-18解：⑴由单缝衍射的暗纹条件bsin=，得≈sin=，则第一级（k=1）暗纹距中心的距离为x1=ftg≈fm⑵由明纹条件，得≈sin=，则第二级（k=2）明纹距中心的距离为x2=ftg≈fm在上述计算中，由于k取值较小，即较小，故。如k取值较大，则应严格计算。对于第二级明纹，有（），，该明纹距中心的距离17-19题中印的条件不足，该题不做。17-20D17-21应用光栅方程得⑴nm=3000nm⑵nm=375nm17-2217-23A17-24解：设入射前一束自然光强为I0入射前另一束自然光强为通过第一个偏振片后光强变为和40\n通过第二个偏振片后光强变为和由已知的两次透射光强相等，得=∴17-25解：设入射的自然光强为I0入射的偏振光强为出射光强：由已知可解得∴18-1B18-2A18-3C40