大学化学-原子结构 89页

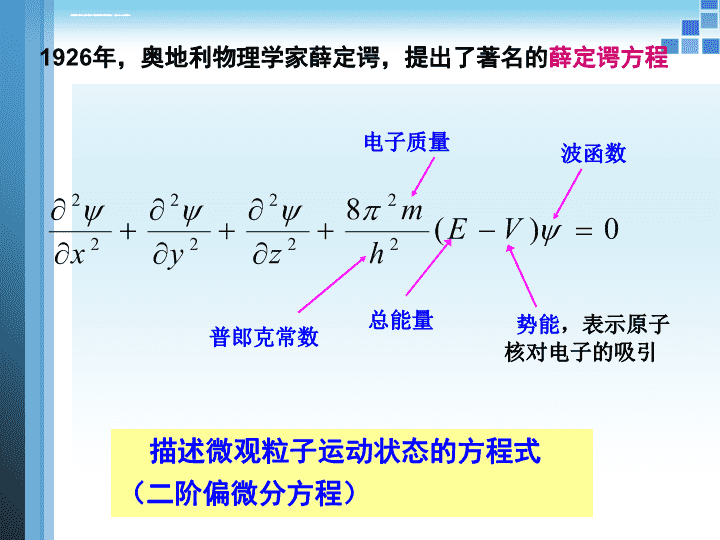
大学化学——原子结构大学化学—原子结构\n核外电子运动状态的描述经典波（如水波）：可用波动方程来准确描述其运动轨迹。具有波粒二象性的电子是否也有相应的波动方程呢?\n1926年，奥地利物理学家薛定谔，提出了著名的薛定谔方程描述微观粒子运动状态的方程式（二阶偏微分方程）势能，表示原子核对电子的吸引总能量普郎克常数电子质量波函数\n原则上讲，只要找出体系势能（V）的表达式，带入薛定谔方程，便可得到波函数（），即求出电子的运动状态。但是，解薛定谔方程并非易事，至今只能求解单电子体系（H,He+,Li2+）的薛定谔方程。在此，我们只用其结论。\n波函数、原子轨道－就是薛定谔方程的解。可见，波函数就是描述核外电子运动状态的数学函数式。(x,y,z)量子力学中，要使所得的解有特定物理意义，中的n,l,m三个量子数必须符合一定条件n,l,m（x,y,z）1、波函数（）\n原子轨道量子力学中，把原子体系的每一个波函数称为一条原子轨道。如n=2，l=0，m=0，波函数2,0,0就称为2s原子轨道因而，波函数与原子轨道同义，常混用。or：原子轨道是由三个量子数（n，l，m）所确定的一个波函数n,l,m（x,y,z）。\n解薛定谔方程可得到一个波函数，也就得到一条原子轨道。四个量子数【即】三个量子数(n,l,m)一定时就确定了一个波函数或一条原子轨道也就确定了核外电子的一种空间运动状态。(1,0,0);(2,0,0);【但是】要使其合理，需要指定三个量子数n，l，m；\n【后来】原子光谱的精细结构表明核外电子除空间运动外，还有一种“自旋运动”，用自旋量子数ms表示。n，l，m，mS称为四个量子数。\n1、主量子数n【意义】描述电子出现概率最大的区域离核的距离，是决定电子能量高低的主要因素（但不是唯一因素）。n越小，电子离核越近，能量越低。n越大，电子离核越远，能量越高。\n【n的取值及符号】1，2，3，4……n正整数光谱学上用K，L，M，N……表示分别称为第一、第二、第三…….第n电子层\n2、角量子数l研究发现，n＝1，只有1种原子轨道n＝2，有2种原子轨道；n＝3，有3种原子轨道为了表示此现象，引入角量子数（l）\n【l的取值及符号】受主量子数n的限制；用s，p，d，f，g……表示。l:0，1，2，3，4……(n-1)，共n个取值。\nl=0：s轨道，形状为球形，即3s轨道；zxsl=1：p轨道，形状为哑铃形，3p轨道;l=2：d轨道，形状为花瓣形，3d轨道;因此，在第三层上，有3种不同形状的轨道（亚层）当n=3时l可取0，1，2\n【l的意义】（1）决定原子轨道（或电子云）的形状，即表示亚层（2）决定电子空间运动的角动量（3）在多电子原子中与n共同决定电子能量的高低【亚层】同一层中(n相同)不同形状的轨道\n第n层有多少个亚层？有n个电子亚层如n=4，l可取0，1，2，3，分别表示4s、4p、4d，4f亚层；【因此】l标志电子亚层\n3、磁量子数mn=2,l=1（2p亚层）,发现在空间有3种不同的取向n=3,l=2（3d亚层）,发现在空间有5种不同的取向为了表示此种现象，引入磁量子数（m）\n【m的取值及符号】受角量子数l的限制对于给定的l，m可取0，1，2，3，…l，共（2l+1）个值。这些取值意味着？在角量子数为l的亚层有（2l+1）个取向，即有（2l+1）条取向不同的原子轨道。\ns轨道：l=0,m=0,只有一种空间取向，所以s轨道为球形。zxs\np轨道：l=1,m=0,+1,-1,在空间有三种取向。\nd轨道：l=2,m=0,+1,-1,+2,-2,在空间有五种取向；\nf轨道：l=3,m=0,+1,-1,+2,-2,+3,-3，七个值在空间有七种取向；f轨道为花瓣形。\n【m的物理意义】描述原子轨道或电子云在空间的伸展方向。每一个m的取值，对应一种空间取向。\nm的不同取值，意味着原子轨道的空间取向不同，但一般不影响能量。【简并】把同一亚层（即l相同），伸展方向不同的原子轨道称为等价轨道或简并轨道。l=1,m=0,+1,-1,有3种空间取向。Px，Py，Pz为3条简并轨道，或者说p轨道是3重简并的。\nd轨道有5种不同的空间取向，d轨道是5重简并的。f轨道有7种不同的空间取向，f轨道是7重简并的。\n【小结】量子数与电子云的关系主量子数n：决定电子云的能量；角量子数l：描述电子云的形状；磁量子数m：描述电子云的空间取向；n,l,m一定，原子轨道也就确定\n4、自旋量子数ms用高分辨光谱仪研究原子光谱时发现：在无外磁场作用时，每条谱线由两条十分接近的谱线组成。为了解释这种现象，认为电子有自旋运动，并提出了自旋量子数，用ms表示。因此，电子既围绕原子核旋转运动，也自身旋转。\nms的取值只有两个：+1/2和-1/2；即电子的自旋方式只有两种，通常用“”和“”表示。\n【注意】【1】指定三个量子数n，l，m，就解出一个波函数（），得到一条原子轨道，因此，可用三个量子数n，l，m描述一条原子轨道；3,0,0,3s轨道；3,1,13p轨道中的一条【2】描述一个电子的运动状态，需要四个量子数，n，l，m，mS。（3,1,0,+1/2）表示在3p轨道上“正旋”的一个电子。\n【四个量子数总结】解薛定谔方程可能得到多个解（），要使解有意义，还取决于n,l,m三个量子数。－n（主量子数）决定电子的能量和离核的远近；－l（角量子数）决定轨道的形状；－m（磁量子数）决定轨道的空间伸展方向；因此，描述一个电子的运动状态需要n，l，m，ms四个量子数为了描述电子的自旋，引入自旋量子数（ms）\n【1】主量子数nn=1,2,3,……;K,L,M,N,…【2】角量子数ll=0,1,2……n-1;s,p,d,f…共n个【3】磁量子数mm=+l,……0,……-l；共2l+1个【4】自旋量子数ms\n概率密度、电子云核外电子没有固定的运动轨迹，只能用统计规律来描述其运动状态。把电子在核外空间某一区域内出现机会的多少，称为概率。电子在核外空间某处单位体积内出现的概率叫概率密度。1、概率密度\n量子力学中，用波函数绝对值的平方表示电子出现的概率密度。因此，空间某点(x,y,z)附近体积内电子出现的概率＝概率密度×体积\n2、电子云化学上习惯用小黑点分布的疏密来表示电子出现几率的大小。可表示电子出现的概率密度，但不直观，较复杂。\n这种形象化表示概率密度分布的图形称为电子云，是电子行为具有统计性的一种形象化描述。小黑点较密的地方，表示该点较大，单位体积内电子出现的机会多，概率密度大。\n【需要注意的是】在研究原子中电子的运动时，无法说明电子恰好在某一位置，只能指出电子在空间的几率密度分布，即电子云分布。\n电子云的角度分布图电子云的角度分布图既Y2(,)对,作图\n几率密度和电子云\n【原子轨道和电子云角度分布图的比较】分布图类似，区别在于：（1）电子云的角度分布图要“瘦”些，∵Y(,)＜1，则Y2(,)更小。（2）原子轨道的角度分布图有正、负之分（不是指带正电或带负电），而电子云的角度分布图全部为正，∵Y(,)平方后总为正值。\n核外电子排布和元素周期律电子在原子核外如何排列？有无规律可言？光谱实验表明：基态原子核外电子的排布有严格规律，首先必须遵循能量最低原理。为此，必须先知道各原子轨道的能级顺序，再讨论电子排布！\n单电子体系：n相同的轨道，能量相同：E4s=E4p=E4d=E4fn越大能量越高：E1sr共\n(3)范德华半径单原子分子(He，Ne等稀有气体)，原子间靠范德华力结合，因此无法得到共价半径。低温高压下，稀有气体能形成分子晶体，原子核间距的一半定义为范德华半径。\n卤素在极低温度下能形成双原子的分子晶体，相邻的不同分子中的两个卤素原子的核间距的一半，就是卤素原子的范氏半径。\n范德华半径（非键合）>金属半径（紧密堆积）>共价半径（轨道重叠）讨论原子半径的变化规律时，常采用共价半径。由此可见：\n(4)原子半径的周期性同周期中，有哪些因素影响原子半径？(a)从左向右，核电荷数（Z），对电子吸引力，r(b)从左向右，核外电子数，电子之间排斥力，r这是一对矛盾，以哪方面为主？以(a)为主。即同周期中从左向右，原子半径减小。\n同族中，原子半径如何变化？(a)从上到下，Z，对电子吸引力，r(b)从上到下，核外电子增多，增加一个电子层，r这一对矛盾中，(b)起主导作用。同族中，从上到下，原子半径一般逐渐增大。主族元素Li123pmNa154pmK203pmRb216pmCs235pm依次增大\n主族元素\n【副族元素和主族元素的情况有所差异】副族元素TiVCrr/pm132122118ZrNbMo145134130HfTaW144134130对于第五、第六周期的副族元素，它们的原子半径非常接近（镧系收缩）\n2、电离能（I）的周期性1mol基态气态原子，失去最高能级的1mol电子，形成1mol气态正离子(M+)所吸收的能量，叫这种元素的第一电离能(用I1表示)。M(g)——M+(g)+eH=I1\n1mol气态M+继续失去最高能级的1mol电子，形成1mol气态M2+所吸收的能量为第二电离能I2M+(g)——M2+(g)+eH=I2用类似的方法定义I3，I4，……In。【可见】电离能（I）表示原子失去电子的能力，I越大，越难失去电子；I越小，越易失去电子。\n失去电子形成正离子后，半径减小，核对电子的引力增加，再失去电子变得困难。对一种元素而言：I12为非金属。\n原子性质从左到右从上到下原子半径减小增大，第五、第六周期接近电离能增大，全满半满结构稍大减小，过渡元素略增，多处不规律电子亲和能增大减小，但O和F并非本族最大值，由于半径小，内层电子排斥力大所致电负性增大减小，副族不明显\n谢谢！