- 2.82 MB
- 2022-08-18 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
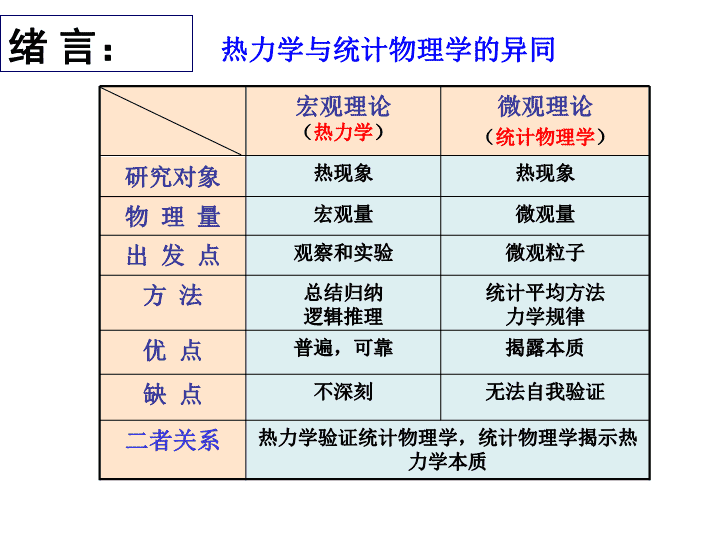
第2章气体分子动理论LudwigBoltzman(1844~1906)玻耳兹曼:奥地利物理学家,统计物理学的奠基人之一。于1868年提出麦克斯韦-玻耳兹曼分布定律。在1872年从非平衡态的分子动力学得到H定理,这是经典分子动力论的基础。1877年提出热力学第二定律与微观几率态数W的关系以及熵的统计解释。1900年普朗克运用玻耳兹曼的理论得出S=klnW并证明了斯忒藩的实验结论u=σT4(斯忒藩-玻耳兹曼黑体辐射公式),掀开了量子时代的帷幕。\n微观粒子观察和实验出发点热力学验证统计物理学,统计物理学揭示热力学本质二者关系无法自我验证不深刻缺点揭露本质普遍,可靠优点统计平均方法力学规律总结归纳逻辑推理方法微观量宏观量物理量热现象热现象研究对象微观理论(统计物理学)宏观理论(热力学)热力学与统计物理学的异同绪言:\n一、分子动理论的三个基本概念宏观物体是不连续的,由大量微观粒子——分子(或原子)所组成物质内的分子在不停地做无规则热运动,其剧烈程度与温度有关\n布朗运动\nOfrr0斥力引力合力分子力表现为斥力分子力表现为引力(平衡位置)分子间有相互作用力r0分子有效直径势能\n二、热运动的特点(1)微观粒子的运动永不停息、无规则,每个粒子的运动过程具有极大的偶然性—无序性。(2)对大量粒子的整体而言,运动又表现出必然的、确定的规律——统计规律。\n一、理想气体的状态方程1.理想气体的概念:是实际气体在一定条件下的近似。实际气体在密度不太高、压强不太大、温度不太低的实验范围内,且遵守玻意耳定律、盖吕萨克定律和查理定律这三条定律的气体。2.理想气体状态方程:R=8.31J/mol·K适用条件:理想气体处于平衡态。T单位为k第一节气体的压强和温度\n1.热力学系统(体系):在热学中所研究的由大量分子、原子组成的物体或物体系。2.平衡态:在不受外界影响或外界条件一定时,系统内处处均匀,其宏观性质不随时间改变的状态。二、热力学系统平衡态状态参量\n(2)平衡态下系统内的分子仍在不停地作无规则运动,只不过大量分子运动的平均效果不随时间改变,因此也叫热动平衡状态。3.状态参量:为描述系统平衡态所具有的特性而引入的参量,如力学参量P、几何参量V、以及热学参量T等。(1)平衡态是一个理想的概念,它是在一定条件下,对实际情况的概括和抽象。\n例2.1设有一端封闭的玻璃管长1m,将它从空气中倒立竖直压入水中直至管的上端露出水面0.2m为止。求水进入管内的深度h(如图)。已知大气压强为1.01325×105Pa,气温为27℃。解:将玻璃管内的气体作为研究对象,并视为理想气体。当玻璃管在空气中时:s为玻璃管的横截面积\n当水进入玻璃管内的深度为h时:由状态方程得:代入数据,解得h≈0.07m,而h≈11.34m不符合题意故水进入管内的深度为h=0.07m\n宏观物体都是由大量不停息地运动着的、彼此有相互作用的分子或原子组成.利用扫描隧道显微镜技术把一个个原子排列成IBM字母的照片.现代的仪器已可以观察和测量分子或原子的大小以及它们在物体中的排列情况,例如X光分析仪,电子显微镜,扫描隧道显微镜等.三、气体动理论的研究方法\n对于由大量分子组成的热力学系统从微观上加以研究时,必须用统计的方法..................................................................................小球在伽尔顿板中的分布规律.\n统计规律当小球数N足够大时小球的分布具有统计规律.设为第格中的粒子数.概率粒子在第格中出现的可能性大小.归一化条件...................................................粒子总数\n统计规律与涨落现象:任一时刻,实际分布在某一速率区间内的分子数,一般来说是与统计平均值有偏离的——涨落现象。\n四、理想气体压强公式的推导(一)、理想气体的微观模型(1)气体分子本身的线度(10-10m)比起分子间的平均距离来说可以忽略不计——可视为质点。(2)除碰撞瞬间外,分子之间及分子与器壁之间的相互作用极其微小,可视为无相互作用,其运动可认为是自由的。(3)气体分子在碰撞中,每个分子都可看作完全弹性的小球,分子的动能不因为碰撞而损失。力学性质的假设:\n(4)气体分子的运动服从经典力学的规律自由地、无规则运动着的弹性质点的集合。统计性的假设:(1)每个分子运动速度各不相同,而且通过碰撞不断发生变化。(2)在平衡态下,若忽略重力的影响,沿各个方向运动的分子数相等。(3)在平衡态下,分子速率按方向的分布是均匀的,因此分子速率的各个分量的方均值应该相等\n压强的宏观解释:对容器内气体的整体而言,每一时刻都有大量分子与器壁发生碰撞,宏观上表现出器壁受到一个恒定的、持续的压力。(二)、压强公式的推导:设在一长方形容器内,有N个同类气体分子,每个分子质量均为m。1)速度为的一个分子与器壁A1面碰撞时给予器壁的冲量A1面沿-X方向给分子的冲量(等于分子动量的改变):\n该分子一次碰撞给予器壁A1面的冲量为2)单位时间内该分子给予A1面的总冲量该分子沿X方向与A1面连续碰撞相隔的时间为单位时间内该分子与A1面碰撞的次数为单位时间内该分子给A1面的总冲量,即对A1面的作用力为\n气体的压强为:3)单位时间内容器内的所有分子施予A1面的总冲量——平均作用力为:其中n为单位体积内的分子数——分子数密度。\n根据统计假设,平衡态下应有:引入分子平均平动动能:理想气体压强公式表示了宏观量P与统计平均值n、平均平动动能之间的关系,是描述大量气体分子整体行为的一个物理量。\n讨论:压强是一个统计平均量,对个别或少数分子是没有意义的。从上推导中可知,压强是容器中大量气体分子在单位时间内施于器壁单位面积的平均冲力(大量分子对时间对空间的统计平均)。\n1、阿伏伽德罗常数:1mol物质所含的分子(或原子)的数目均相同.例常温常压下分子数密度():单位体积内的分子数目.五、分子的平均平动动能与温度的关系\n2、温度的本质和统计意义\n玻尔兹曼常数温度公式微观量宏观量揭示了气体温度的统计意义,即气体的温度是气体分子平均平动动能的量度,它是描述大量分子热运动剧烈程度的物理量。\n2、气体分子的方均根速率(2)将温度公式代入压强公式得:(1)分子热运动永不停止,所以绝对零度永远不可能达到。得,方均根速率注意:由平均平动动能\n例求00C时氢气和氧气分子平均平动动能。解:气体分子平均平动动能只与温度有关3、道尔顿分压定律设有多种相互不发生化学反应的气体在一容器中混合,达平衡态,则混合气体压强为\n\n一、自由度i确定一个物体的空间位置所需要的独立坐标数目。1.质点的自由度在空间自由运动的质点:在曲面上运动的质点:质点沿直线或曲线运动:位置由一个独立坐标确定自由度i=1位置由三个独立坐标确定自由度i=3位置由二个独立坐标确定自由度i=2第二节能量按自由度均分定理\n①质心→自由质点②绕质心轴的转动③转轴的方位2.刚体的自由度\n刚性分子:分子内原子间距离保持不变双原子分子单原子分子平动自由度t=3平动自由度t=3转动自由度r=23.刚性分子的自由度\n三原子分子平动自由度t=3转动自由度r=3二、能量按自由度均分定理\n推广气体分子沿x,y,z三个方向运动的平均平动动能完全相等,可以认为分子的平均平动动能均匀分配在每个平动自由度上。—能量按自由度均分定理在热平衡条件下,物质(气体、液体、固体)分子的每一个自由度都具有相同的平均动能,都是。\n若气体分子有t个平动自由度,r个转动自由度,s个振动自由度,则分子的平均平动动能,平均转动动能为,平均振动动能为。分子的平均总动能为:分子的平均总能量为:\n对于单原子分子:t=3,r=s=0,则对于刚性双原子分子:t=3,r=2,s=0,则对于刚性多原子分子:t=3,r=3,s=0,则对于刚性分子:忽略振动,s=0,则\n质量M理想气体的内能为内能仅与温度有关,当温度一定时,与压强和体积无关。温度改变量为△T,则内能改变量为1mol理想气体的内能为理想气体的内能=所有分子的热运动动能和原子间振动势能的总和分子间相互作用忽略不计分子势能为零三、理想气体的内能内能为温度的单值函数。\n例2.2一个贮有氮气的容器以速率v0=200m·s-1运动,若该容器突然停止。试求容器中氮气的温度和速率的平方平均值的变化。解:设氮气的质量为M,摩尔质量为µ,视氮气为由刚性氮分子组成的理想气体。由题意得(1)\n式中m为氮分子的质量(2)由(1)、(2)两式联立求解,并将代入上式表明:双原子分子速率平方的平均值的增量等于该容器定向运动速率平方的3/5。即表示定向运动动能的3/5转换成分子的平均平动动能,其余2/5则转换成分子转动的平均动能。\n补例一容器内蓄有氧气,其压强为P=1.013×105Pa,温度为27℃,求:(1)单位体积内的分子数;(2)氧气的密度;(3)氧气分子的质量;(4)分子的平均平动动能;(5)分子的平均总动能。解:氧气分子视为刚性双原子分子,i=5\n注意:①“分子的”→微观量→k②“气体的”→宏观量→R\nf(v)满足归一化条件:一、速率分布函数一定量理想气体处于平衡态,设有N个分子,速率分布在v~v+dv区间内的分子数为dN,则为在此区间内的分子数比率。实验证明:①与v的一定函数f(v)成正比;②与v附近取的区间dv大小成正比。则,称为速率分布函数。已知f(v),则可求任意速率区间内的分子数:第三节麦克斯韦速率分布率\n1860年,麦克斯韦导出f(v)的表达式麦克斯韦气体分子速率分布定律T----温度m----气体分子质量k----玻尔兹曼常数由此,得分布在v~v+dv内的分子数比率:二、麦克斯韦气体分子速率分布定律1.麦克斯韦速率分布\n2.麦克斯韦速率分布函数的几何意义vv+dvvN出现在v~v+dv区间内的分子数比率dN面积=v1v2出现在v1~v2区间内的分子数比率大部分分子的速率分布在中等区域气体分子的速率分布曲线下面积\n最概然速率:与f(v)极大值对应的速率对于相同速率区间而言,分布在vp所在的那个区间内的分子数比率最大。或者说某一分子的速率取Vp所在区间的值的几率最大。\n1.最概然速率与分布函数f(v)的极大值相对应的速率极值条件2.平均速率大量分子速率的统计平均值三、分子速率的三种统计平均值设在v~v+dv内有dN个分子,这些分子的速率视为相同,则\n3.方均根速率大量分子速率的平方平均值的平方根\n都与成正比,与(或)成反比f(v)v一定温度时,\n温度越高,速率大的分子数越多.温度升高,分布曲线中的最可几速率vp增大,但归一化条件要求曲线下总面积不变,因此分布曲线变平坦,高度降低。f(v)f(vp3)vvpf(vp1)f(vp2)T1T3T2\n讨论麦克斯韦速率分布中最概然速率的概念下面哪种表述正确?(A)是气体分子中大部分分子所具有的速率.(B)是速率最大的速度值.(C)是麦克斯韦速率分布函数的最大值.(D)速率大小与最概然速率相近的气体分子的比率最大.\n例计算在时,氢气和氧气分子的方均根速率.氢气分子氧气分子\n1)2)例已知分子数,分子质量,分布函数求1)速率在间的分子数;2)速率在间所有分子动能之和.速率在间的分子数\n例如图示两条曲线分别表示氢气和氧气在同一温度下的麦克斯韦速率分布曲线,从图上数据求出氢气和氧气的最可几速率.2000\n设分子速度大小为v,B到C所需的时间为t,只有满足vt=l、ωt=φ关系的分子才能到达C的狭缝射到显示屏上。四、分子速率的实验测定\n实验装置测定气体分子速率分布的实验金属蒸汽显示屏狭缝接抽气泵改变ω(或l、φ)可使速度大小不同的分子通过C,故又称为速度选择器。\n在麦克斯韦速度分布律中,考虑了分子速度方向,则速度分布在vx~vx+dvx,vy~vy+dvy,vz~vz+dvz内的分子数比率为:其中一、玻尔兹曼能量分布律1.麦克斯韦速度分布律第四节气体分子能量分布的统计规律→,\n2.玻尔兹曼分布律玻尔兹曼对麦克斯韦速度分布律作了推广:(1)分子在保守力场中(2)分子的分布不仅按速度区间v~v+dv分布,还应按位置空间x~x+dx,y~y+dy,z~z+dz分布。当系统在保守力场中处于平衡态时,速度在\n玻尔兹曼分子按能量分布律其中n0为零势面处的分子数密度.将上式对所有可能的速度积分,并考虑归一化条件:\ndN分布在坐标区间x~x+dx,y~y+dy,z~z+dz内小体积元dxdydz中具有各种速度的分子总数。该区间的分子数密度为:这是玻尔兹曼分子数密度按势能的分布律,在任何保守力场中都成立。它又是一普遍规律,对任何物质微粒在保守力场中运动的情形都适合。n0势能等于零处的分子数密度\n由玻尔兹曼分布律证明等温气压公式式中P0为h=0处的大气压强,P为h处的大气压强,m是大气分子质量。证:由方程大气分子数密度和压强随高度增加按指数规律减小(高空空气稀薄,气压低)二、等温气压公式\n气体分子平均速率氮气分子在270C时的平均速率为476m.s-1.矛盾气体分子热运动平均速率大,但气体扩散过程进行得相当慢。气体分子的速度虽然很大,但前进中要与其它分子作频繁的碰撞,每碰一次,分子运动方向就发生改变,所走的路程非常曲折。第五节气体分子碰撞的统计规律\n在相同的t时间内,分子由A到B的位移比它的路程小得多扩散速率(位移/时间)平均速率(路程/时间)分子平均自由程:气体分子在连续两次碰撞之间平均自由通过的路程。平均碰撞频率:在单位时间内分子与其它分子碰撞的平均次数。\n大量分子的分子自由程与每秒碰撞次数服从统计分布规律。可以求出在一秒钟内一个分子与其他分子碰撞的平均次数和分子自由程的平均值。平均自由程平均自由程的大小是一定的假定每个分子都是有效直径为d的弹性小球只有某一个分子A以平均速率运动,其余分子都静止。\nAdddvv在运动方向上,以d为半径的圆柱体内的分子都将与分子A碰撞球心在圆柱体内的分子一秒钟内:分子A经过路程为相应圆柱体体积为圆柱体内分子数一秒钟内A与其它分子发生碰撞的平均次数\n一切分子都在运动一秒钟内分子A经过路程为一秒钟内A与其它分子发生碰撞的平均次数平均自由程平均自由程与分子的有效直径的平方及分子数密度成反比当温度恒定时,平均自由程与气体压强成反比\n例2.4计算空气分子在27℃,压强为1atm时的平均自由程和平均碰撞频率。取分子的有效直径d=3.010-10m。已知空气的平均分子量为2910-10m。(P54)解:\n在标准状态下,几种气体分子的平均自由程气体氢氮氧空气补例计算空气分子在标准状态下的平均自由程和平均碰撞频率。取分子的有效直径d=3.1010-10m。已知空气的平均分子量为29。解:已知\n空气摩尔质量为2910-3kg/mol空气分子在标准状态下的平均速率\n在许多实际问题中,气体常处于非平衡状态,气体内各部分的温度或压强不相等,或各气体层之间有相对运动等,这时气体内将有能量、质量或动量从一部分向另一部分定向迁移,这就是非平衡态下气体的迁移现象。粘滞现象(内摩擦)动量从流速大的气层向流速小的气层迁移的现象。第六节气体的输运过程第六节气体分子碰撞的统计规律\n气体层间的粘滞力气体粘滞现象的微观本质是分子定向运动动量的迁移,而这种迁移是通过气体分子无规热运动来实现的。AB为粘度(粘性系数)\n二热传导现象AB**设气体各气层间无相对运动,且各处气体分子数密度均相同,但气体内由于存在温度差而产生热量从温度高的区域向温度低的区域传递的现象叫作热传导现象。气体热传导现象的微观本质是分子热运动能量的定向迁移,而这种迁移是通过气体分子无规热运动来实现的。称为热导率\nAB**三扩散现象自然界气体的扩散现象是常见的现象,气体扩散现象的微观本质是气体分子数密度的定向迁移,而这种迁移是通过气体分子无规热运动来实现的。为扩散系数\n气体扩散现象的微观本质是气体分子数密度的定向迁移,而这种迁移是通过气体分子无规热运动来实现的.AB**四三种迁移系数扩散系数热导率粘度(粘性系数)\n小结一、基本概念及公式气体动理论的基本概念物质的微观结构(3点);气体动理论的统计规律性;热力学系统,平衡态;理想气体的微观模型(4点)。\n分子的平均碰撞次数2.理想气体状态方程3.阿伏伽德罗定律4.理想气体压强公式5.理想气体温度公式6.分子的平均自由程\n(3)三种速率:二、三个统计规律速率分布律及应用:(1)速率分布函数:(2)麦克斯韦速率分布函数:\n三.能量按自由度均分定理自由度i:确定一个物体的空间位置所需要的独立坐标数目。单原子分子:i=3双原子分子:i=5三原子或三原子以上的多原子分子:i=6能量按自由度均分定理:在热平衡条件下,物质(气体、液体、固体)分子的每一个自由度都具有相同的平均动能,都是。\n理想气体分子的:(1)平均总动能:(2)平均平动动能:1mol理想气体的内能:M质量理想气体的内能:气体内的三种输运过程:内摩擦现象、热传导现象、扩散现象