[农学]叶宏工程硕士第4次 38页

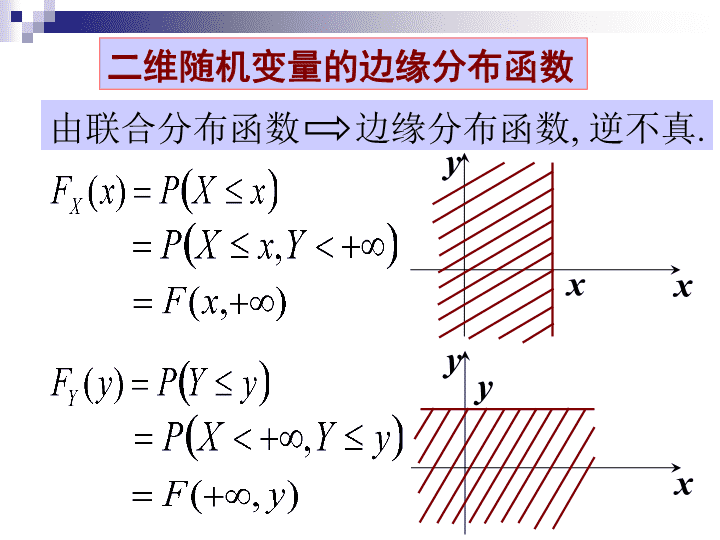
5.2边缘分布边缘分布函数边缘分布律边缘概率密度\n边缘分布边缘分布也称为边沿分布或边际分布\n二维随机变量的边缘分布函数xyxxyy由联合分布函数边缘分布函数,逆不真.\n二维离散型随机变量的边缘分布由联合分布律可确定边缘分布律\n1x1xipi•p1•pi•p•jp•1p•jyjy1XY联合分布律及边缘分布律\n例箱子里装有4只白球和6只红球，在其中随机地取两次，每次取一只。考虑两种试验：（1）有放回抽样，（2）不放回抽样。我们定义随机变量X，Y如下，写出X和Y的边缘分布律。\n（1）有放回抽样YX01011\n（2）不放回抽样YX10101\n已知联合密度可以求得边缘密度二维连续型随机变量的边缘分布\nyoy=x21x\nyoy=x21x\nyoy=x21x\n例\n\n结论（一）结论（二）\nP100例5(1)(2)(3)法1：法2：利用分布函数\n条件分布律条件分布函数条件概率密度5.3条件分布\n在第一章中，我们介绍了条件概率的概念.在事件B发生的条件下事件A发生的概率推广到随机变量设有两个随机变量X,Y，在给定Y取某个值的条件下，求X的概率分布.这个分布就是条件分布.\n一.离散型随机变量的条件分布律设(X,Y)是离散型随机变量，其分布律为P(X=xi,Y=yj)=pij,i,j=1,2,...(X,Y)关于X和关于Y的边缘分布律分别为：\n由条件概率公式自然地引出如下定义：定义：设(X,Y)是二维离散型随机变量，对于固定的j,若P(Y=yj)>0,则称为在Y=yj条件下随机变量X的条件分布律.\n同样对于固定的i,若P(X=xi)>0,则称为在X=xi条件下随机变量Y的条件分布律.\n1联合分布与边缘分布\nX123将表中第一列数据代入得条件分布\n二.连续型随机变量的条件分布设(X,Y)是二维连续型随机变量，由于P(X=x)=0,P(Y=y)=0所以不能直接代入条件概率公式，先利用极限的方法来引入条件分布函数的概念。由条件分布函数可以引出条件概率密度\n在条件Y=y下X的条件分布函数\n定义\n例已知求解\n同理，\n一般题型见P108.1\n5.4随机变量的独立性两事件A,B独立的定义是：若P(AB)=P(A)P(B)则称事件A,B独立.设X,Y是两个r.v，若对任意的x,y,有则称X,Y相互独立.两随机变量独立的定义是：\n用分布函数表示,即设X,Y是两个r.v，若对任意的x,y,有则称X,Y相互独立.它表明，两个r.v相互独立时，联合分布函数等于两个边缘分布函数的乘积.\nX与Y独立即对一切i,j有离散型\n连续型二维随机变量(X,Y)相互独立,则边缘分布完全确定联合分布X与Y独立对任何x,y有\n二维连续r.v.(X,Y)相互独立\nP108.1\nX和Y相互独立\nX和Y相互独立或者由独立性\n5.5多维随机变量简述