【5A版】信息经济学-信息经济学研究方法 84页

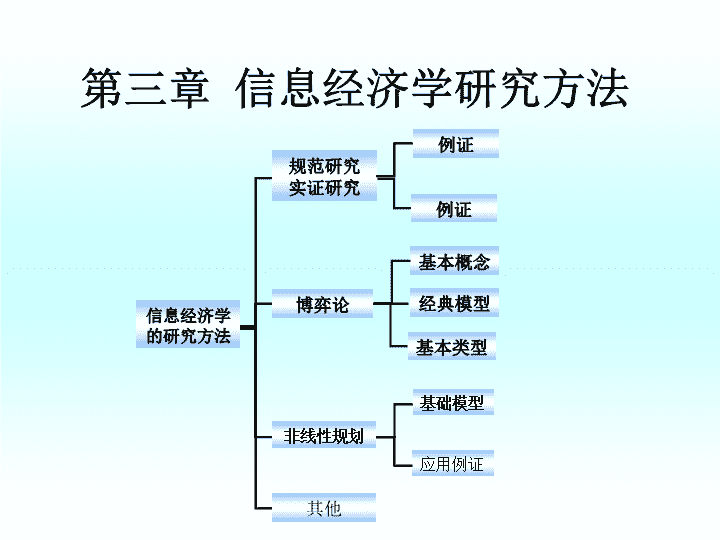
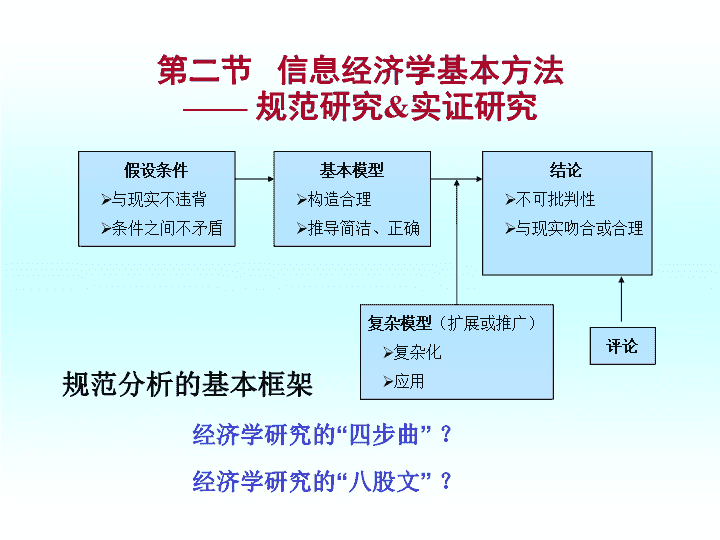
第三章信息经济学研究方法博弈论基本概念规范研究实证研究非线性规划应用例证基础模型其他例证基本类型信息经济学的研究方法例证经典模型\n第二节信息经济学基本方法——规范研究&实证研究假设条件与现实不违背条件之间不矛盾基本模型构造合理推导简洁、正确结论不可批判性与现实吻合或合理复杂模型（扩展或推广）复杂化应用评论规范分析的基本框架经济学研究的“四步曲”？经济学研究的“八股文”？\n1.规范研究的假设条件在信息经济学之前，微观经济学假设中几乎都包括经济人假设和完全信息假设这两个最基本的假设。经济人假设也称为理性人假设，是指经济决策主体（消费者、生产者等）的经济行为都是理性的或合乎理性的，他们在经济活动中不会感情用事，而是精于判断和计算，总是以利己为动机，力图以最小的经济代价去追逐和获得自身的最大利益。完全信息假设是指经济活动的所有当事人都拥有充分的和相同的信息，而且获取信息不需要支付任何成本。其它假设：完全竞争假设、稀缺性假设（资源不能够满足人们不断增长的需求）、制度假设（既定的市场经济制度）、交易成本为零的假定\n完全信息——不完全信息阿克洛夫首先提出的不对称信息市场更好的贴近了现实，更为准确地反映了市场上商品的异质性。古典假设的错误？经济学规范研究的模型假设两方面要求：一是与现实不违背，二是条件之间不矛盾。完全信息假设可以满足这两方面要求，甚至可以说，正是这种由简单到复杂的假设扩展过程使经济学的发展更为平稳和完备。\n2.模型建立的典范——一般均衡分析里昂•瓦尔拉斯（LeonWalras，1834~1910）里昂·瓦尔拉斯，法国经济学家，边际革命领导人，洛桑学派创始人。19世纪50年代开始研究政治经济学，1870年被聘为洛桑大学政治经济学教授。瓦尔拉斯是边际效用价值论的创建人之一，他把边际效用称为“稀少性”，并在经济学中使用了数学，研究了使一切市场(不是一种商品的市场，而是所有商品的市场)都处于供求相等状态的均衡，即一般均衡，从而成为数理经济学和一般均衡理论的创建者和主要代表，他的一般均衡分析方法被经济学所普遍使用。瓦尔拉斯把自由竞争的资本主义看作最理想的制度，但也主张国家根据正义原则干预经济。\n实证研究的框架理论分析提出假说构建模型实证分析收集数据数据处理计量检验结论作出预测给出问题的对策文献综述研究方法研究结论讨论反映现实？预测未来？实证研究能够实现：讨论区\n第二节信息经济学基本方法——博弈论经济学研究的基本问题：——资源的有效配置——人的行为经济学的基本假设：人是理性的理性人：在一定的约束条件下，使自己的收益最大化。\n新古典经济学：价格制度——每个参与者的决策是独立的。基本假设：（1）市场是竞争的（2）信息是完全的（3）产品是独立的个人决策的分析：收入—支出（价格），收益最大化博弈论：基本假设：（1）市场是不完全竞争的（2）信息是不完全的特征：每个参与者的决策是相互影响的\n博弈：国家之间、企业之间、人与人之间生活中的博弈：——打牌、下棋——宿舍打扫卫生——宿舍买电风扇——家庭装修——挤公共汽车\n一、经济博弈论的产生与发展通常，人们将数学家冯•诺依曼（vonNeumann）于1928年提出的二人零和博弈的极小化极大定理作为博弈论奠基的标志。1944年，数学家冯•诺依曼（vonNeumann）和经济学家摩根斯坦恩（Morgenstern）合作发表了《博弈论和经济行为》一书，被认为是应用博弈论进行经济分析的开始。20世纪50-60年代，博弈论确立了发展的基础。1950-1951年，Nash发表了两篇关于非合作博弈的重要论文。1950年，Tucker定义了“囚犯难题”（prisoners’dilemma）。Nash和Tucker的工作基本奠定了现代博弈论的基础。20世纪60年代，泽尔腾（Selten）将纳什均衡的概念引入了动态分析。1967-1968年，海萨尼（Harsanyi）发表了《具有不完全信息的由Bayesian局中人所进行的博弈》。此后，他们两人长期合作，发展了非合作博弈理论。\n1994年诺贝尔经济学奖获得者：美国数学家JohnF.Nash，德国经济学家ReinhardSelten，美籍匈牙利经济学家JohnC.Harsanyi。1928年Nash出生于美国，1950年获Princeton大学数学博士学位，曾先后任教于MIT和Princeton大学。其博士论文《非合作博弈》首次区分了合作博弈与非合作博弈，并且提出了非合作博弈的所谓Nash均衡概念。1930年Selten出生于现属于波兰的德国城市，1961年获法兰克福大学数学博士学位，曾先后任教于柏林自由大学、比勒菲尔特大学和波恩大学。其主要贡献是在博弈论中引入了动态分析。1920年Harsanyi出生于匈牙利，1947年获布达佩斯大学博士学位，后到美国，1954年获斯坦福大学博士学位，曾先后任教于澳大利亚国立大学、加州伯克利分校。于2000年去世。他的贡献是将不完全信息引入了博弈论的研究。\n二、经济博弈论主要概念及表述（一）博弈的基本概念局中人（players）：指做决策的个体。每个局中人的目标都是通过选择行动来使自己的效用最大化。虚拟局中人（pseudo-players）：指以一种纯机械的方式来采取行动的个体。自然是一种虚拟局中人，它在博弈的特定时点上以特定的概率随机选择行动。例如：——你要出门，要决策是否带伞——打牌\n行动（actions）：是指局中人的决策变量。局中人i的行动以ai表示，是他所能做的某一选择。局中人i的行动集（actionset）是其可以采用的全部行动的集合。一个行动组合（actionprofile）是一个由博弈中的n个局中人每人选择一个行动所组成的有序集。例如：——出门：带伞或不带伞——打牌：出牌\n信息（information）指局中人在博弈中的知识，特别是有关其他局中人（竞争者或对手）的特征和行动的知识。一般地，信息是以信息集（informationset）的概念来模型化的。可以将局中人的信息集看成是其在特定时点对于不同变量的取值的了解程度。例如：——对天气的判断（出门）——对其他人的判断（打牌）——对产品了解的程度（装修）\n战略（strategies）或策略，是局中人选择行动的规则，它告诉局中人在什么时候选择什么行动。例如：——“人不犯我，我不犯人；人若犯我，我必犯人”——三个和尚没水喝\n支付（payoff）：指每个参与人从博弈中获得的效用水平。既可以指实际支付，也可以用来指期望支付。它是所有局中人战略或行动的函数，是每个局中人关注的核心问题。例如：——出门带伞的成本为2，如果下雨，有伞获得的收益为6，则实际得到的效用为4。结果（outcome）是指在博弈结束后，建立博弈模型者从行动、支付和其他变量的取值中所挑选出来的他所感兴趣的要素的集合。\n均衡（equilibrium）：指所有局中人的最优战略组合或行动组合。或者，均衡s*=（s1*，…，sn*）指由博弈中的n个局中人每人选取的最佳战略所组成的一个战略组合。局中人B左右上2，10，0局中人A下0，01，2小丽足球芭蕾足球2，10，0大林芭蕾0，01，2\n小结：一个博弈中需要的要素包括：局中人、行动、信息、战略或策略、支付、结果和均衡。其中，对一个博弈的描述至少必须包括：局中人、战略和支付。局中人、行动和结果合起来统称为博弈规则（rulesofthegame），博弈分析的目的在于运用博弈规则来确定均衡。惟一性（uniqueness）：公认的均衡概念并不能保证惟一性，缺乏惟一性是博弈论的主要缺陷或问题。例如，可能存在多种均衡，或者根本就没有均衡。解决方案：看重博弈的规则，而不是均衡概念。\n（二）博弈的基本表述双变量矩阵表：双变量指在两个局中人的博弈中，每一单元格都有两个数字——分别表示两个局中人的收益。局中人B左右上2，10，0局中人A下0，01，2博弈表述的基本要素包括：局中人、战略和支付\n（三）划分博弈的主要概念1.合作博弈与非合作博弈合作博弈（cooperativegame）：是以局中人整体的可能联合行动集合为基本要素。通俗地说，如果局中人能够达成有约束力的协议或合约，则该博弈称为合作博弈。合作博弈强调的是集体理性。非合作博弈（non-cooperativegame）：是以单个局中人的可能行动集合为基本要素的博弈。通俗地说，如果局中人不能在博弈中达成有约束力的协议或合约，则称该博弈为非合作博弈。非合作博弈强调的是个体理性。信息经济学主要研究的是非合作博弈。\n2.零和博弈与非零和博弈按照博弈的收益分配结果划分，博弈可以划分为零和博弈和非零和博弈。零和博弈指在博弈中一组局中人所得到的支付（或收益）恰好是另一组局中人的损失。通俗地说，博弈结果总和为零的博弈称为零和博弈。非零和博弈指所有局中人的支付（或收益）的代数和不为零。为正或为负。例如：赢钱与输钱为零和博弈；工会与厂方达成增加工资的协议双方获得“双赢”。反之，罢工导致“两败俱伤”。3.自然假设与自然参与博弈\n4.根据信息结构划分对称信息（symmetricinformation）：指博弈中任一局中人都至少包含与其他每个局中人的信息集相同的元素。非对称信息（asymmetricinformation）：指至少有一个局中人拥有私人信息（privateinformation）。完全信息（completeinformation）：指局中人完全了解其他局中人的收益或收益函数。通俗地说，局中人完全了解其他局中人的特征、战略空间及支付函数。不完全信息（incompleteinformation）：指至少有一个局中人不完全了解其他局中人的收益或收益函数。\n完备信息（perfectinformation）：指一个参与人对其他参与人的行动选择有准确的了解。不完备信息（Imperfectinformation）：指博弈中至少有一个局中人不了解其他局中人的行动选择。完全信息——如“石头、剪刀、布”游戏不完全信息——如打牌完备信息——“石头、剪刀、布”游戏中，你知道对方40%出石头，30%出布，30%出剪刀\n5.根据行动结构划分静态博弈（staticgame）：博弈中局中人同时选择行动，或虽然不是同时行动但后行动者并不了解前行动者采取了什么具体行动。例如：——“石头、剪刀、布”的游戏——应聘者演讲（轮流，但其他人在外等候）讨论：1）田忌赛马的博弈是否属于静态博弈？2）企业中有哪些属于静态博弈的例子？3）当你知道对方40%出石头，30%出布和30%出剪刀，但不知道组合的顺序，你的最优策略是什么？\n动态博弈（dynamicgame）：指局中人的行动有先后顺序，且后行动者能够观察到先行动者所选择的行动。例如：——下棋、打牌等游戏——应聘者演讲（轮流，但后者可以听前者的演讲）——博士答辩的安排顺序政府政策与企业行为之间“上有政策，下有对策”博弈：——关税水平与走私、税收与逃税之间的博弈；——政府与企业之间“鞭打快牛”的博弈；——政府官员“四菜一汤”规定的博弈。\n基于信息结构和行动结构来划分博弈的结果：博弈的类型及对应的均衡概念行动顺序静态结构动态结构信息（战略博弈）（扩展博弈）完全信息静态博弈完全信息动态博弈完全信息结构Nash均衡子博弈精练Nash均衡Nash(1950,1951)Selten(1965)不完全信息静态博弈不完全信息动态博弈不完全信息结构贝叶斯Nash均衡精练贝叶斯Nash均衡Harsanyi(1967-1968)Selten(1975)等\n信息结构与行动结构框架图静态结构动态结构（战略博弈）（扩展博弈）完全信息结构石头/剪刀/布围棋、象棋不完全信息结构赌博黔驴技穷\n6.博弈类型的另一种划分方法：局中人1人博弈2人博弈多人博弈（个人与自然）零和ACE博弈结果非零和BDF\n1人博弈：个人与自然假设一位花农需要决定种植花的品种，但无法知道明年的天气情况，通过经验和资料得知明年各种天气类型出现的可能性是：S1=0.2，S2＝0.1，S3＝0.4，S4＝0.3。可以选择的花的品种为3种。不同的花在不同的气候条件下的收成为：S1S2S3S4A1121090A28844A3161232概率0.20.10.40.3如果只能选择一种花的话，花农应该选择种哪种花？期望值（A1）、大中最大（A3）、小中最大（A2）天气品种\n三、经典博弈思想及其应用（一）完全信息静态博弈：Nash均衡1.Nash均衡的概念通俗地说，Nash均衡是指由全部局中人的最优战略组成的均衡。在其他局中人战略既定的情况下，没有任何单个局中人会选择其他战略，从而没有任何局中人会打破这种均衡。Nash均衡是一个稳定状态的解。在这个（“僵局”）状态下，每个局中人的决策依赖于均衡的知识。\n2.Nash均衡的主要特征（1）Nash均衡可能是高成本的（2）可能不存在纳什均衡（3）Nash均衡可能有多重解\n3.Nash均衡：囚犯难题张三坦白不坦白坦白-3,-30,-6李四不坦白-6,0-1,-1\n囚犯难题的推论：1）可能不是帕累托最优；2）个体理性与集体理性的不一致性；3）表明制度安排的重要性；4）在现实政治经济中，合作具有积极普遍的意义。囚犯难题的应用：——军备竞赛——企业员工——交通堵塞——经济改革——投票选举\n囚犯难题应用1：军备竞赛20多年前，美、苏两国是两个超级大国，他们相互对垒。假设他们有两种策略选择：扩军或裁军。双方选择的支付如下：苏联扩军裁军扩军-2000，-20008000，-∞美国裁军-∞，80000，0\n囚犯难题应用2：环境保护两个企业（u1，u2）被问：是否同意建造一个新的下水管道以使地下水不被污染。假设建造下水管道需要投资120万。如同意各承担50%，下水管道对企业的价值分别是80万。说明：产权界定与环境保护的制度建设对于公共资源的保护是十分必要的。\n囚犯难题应用3：搭便车分析假设：学生A和B各有财产300元；对风扇的福利评价分别为100元，风扇价格为160元，合伙买风扇的收益为200-160=40元。学生B买风扇不买风扇买风扇320，320240，400学生A不买风扇400，240300，300\n现实中的搭便车现象：——灯塔、路灯等公共设施；——污染等环境问题；——各种滥竽充数的广告、产品或服务。搭便车问题的主要解决方案：——中央集权制；——投票制：少数服从多数；——征收克拉克税（如汽油税、过桥费）。\n4.不存在Nash均衡：保安与小偷基本假设：策略；预期效益。小偷不偷偷不睡觉0,00,-1保安睡觉1,0-1,3\n猜硬币博弈：每个局中人的战略空间为（正面，背面）局中人2正面背面正面-1，11，-1局中人1背面1，-1-1，1在博弈中，一旦每个局中人都竭力猜测其他局中人的战略选择，就不存在Nash均衡（至少不存在前面定义的标准的Nash均衡）。因为这时局中人的最优行动是不确定的，而博弈的结果必然要包含这种不确定性。例如：股票市场\n5.Nash均衡：智猪博弈（boxedpigs）假设按一下按钮要支付2个单位成本，有10个单位猪食进入猪槽。又假设：1）大猪和小猪同时赶到，大猪吃7个单位，小猪吃3个单位；2）大猪和小猪同时按按钮又同时赶到猪槽，扣除2个单位成本后，大猪支付水平为7-2=5，小猪支付水平为3-2=1。3）大猪按按钮，小猪等待，小猪先赶到，小猪吃4个单位，大猪吃6个单位。大猪支付水平为6-2=4，小猪支付水平为4-0=4。4）小猪按按钮，大猪等待，大猪先赶到，大猪吃9个单位，小猪吃1个单位。大猪支付水平为9-0=9，小猪为1-2=-1。大猪按等待按1，5-1，9小猪等待4，40，0\n智猪博弈表明：能者多劳，但多劳者未必多得。在每个行业中龙头企业都要承担三个“大猪成本”：1）市场开拓成本——群狼策略；2）人才培训成本——猎头策略；3）商业模式创新成本——模仿策略。例如，“大猪控股”和“小猪有限”都计划引进一种新产品，但为了获得公众的认同，须投入广告费用。如大猪控股打头阵，小猪有限跟进也可以获得一部分市场。相反，如小猪有限先进入，大猪控股就会后发制任，独占市场。现实生活中的智猪博弈例子：——领头企业与小企业（麦当劳与小快餐店）——股票市场上的大户与小户——企业的大股东和小股东——公共设施或基础设施投资：富人与穷人的博弈\n6.Nash均衡：性别之战（battleofthesexes）假设条件：1）联合行动收益大于非联合行动收益；2）非合作基础：影响力或影响因子相同。丈夫足球芭蕾足球2,3-1,-1妻子芭蕾1,13,2\n评论：在性别之战中，任一Nash均衡都是帕累托最优，其他任一战略组合都不可能在不降低其他局中人支付的条件下提高另一局中人的支付。问题：在性别之战的两个Nash均衡中，究竟最终是哪个？情形一：彼此不沟通，出现非联合行动；情形二：可以通过博弈的重复进行形成共同知识（commonknowledge），也有可能出现Nash均衡；情形三：局中人不沟通，但每晚重复进行这一博弈，他们将最终稳定在某一Nash均衡上。\n性别之战应用：菜市场早市/夜市博弈假设两个相互竞争的蔬菜市场可以自己决定是开早市还是开夜市，但每个市场一天只能开一次。如果是开夜市，蔬菜就可以通过船运，如果是开早市，就必须通过货车运输。船运会比车运便宜。中国家庭主妇虽然传统上习惯早上买菜，但如果菜价在夜市便宜许多，她们也有可能到夜市买菜。无论如何一户一天只买一次菜（数学上称为不重叠组合）。问题：两个菜市场如何决定开早市还是开夜市，在决定之前是否应该相互合作？各种支付如下图。\n性别之战策略：（1）先动优势A企业民用市场军用市场民用市场-10，-1030，15B企业军用市场15，30-10，-10（2）公平性合作战略（3）补偿性合作战略（4）随机行动策略（“李王庄”车站）\n7.Nash均衡：勇士博弈勇士博弈是反映20世纪50年代美国青年的行为特征，并通过JameDean主演的电影典型地表现出来：某个青年集团中有A和B两人争斗集团头领。他们将通过一个勇气的测验来决定谁更勇敢，勇敢者就可以当头领。测验规则如下：A与B各自驾驶自己的小车在一条道路上面对面朝对方高速开去，谁第一个让开谁就输掉。让开者被称为胆小鬼（chicken）而不能当头领。如果两人都不让开，结果是车毁人亡。如果两人同时让开，结果是平局。如果一方让开一方不让，让开者则既丢面子，又当不成头领。勇士博弈的支付矩阵如下。\n勇士博弈模型：局中人B前进避让前进0，08，2局中人A避让2，86，6现实生活中的勇士博弈例子：——警察与游行队伍——夫妻吵架——产品销售中的竞争勇士博弈中的有效策略：恫吓或威慑\n课堂讨论：——路灯维修——道路铺设——囚徒博弈——智猪博弈——勇士博弈\n8.Nash均衡：市场进入阻挠（entrydeterrance）假设局中人A为潜在市场进入者，局中人B为现有市场的占有者。具体博弈模型如下所示：局中人B：占有者接纳竞争进入20，30-10，0局中人A：进入者不进入0，1000，100\n9.Nash均衡：聚点（focalpoints）在以下的选择中，如果你的选择与其他局中人的选择一致的次数越多，你就赢得越多，那么，你在博弈中将采取什么战略？（1）选择下述一个数并画圈：7，100，13，261，99，666。（2）你要在中山大学与一个没有来过中山大学的高中同学会面，应在什么时间、什么公共地点碰面？（3）选择下述一个数并画圈：14，15，16，17，18，100。（4）你与另外一人一起分蛋糕，你们各自报出期望分到的比例，但如果你们报的比例之和超过100%，大家都将一无所获。（5）假设你到一个热带岛国去做市场营销，只允许带一样产品，你会选择带什么产品？\n聚点：就是出于心理或其他非理性原因受到人们共同关注的那些Nash均衡。评论1：在上述博弈中，每一个题目都有许多Nash均衡。但是，在这些Nash均衡中，总有一些看起来或多或少可能性会更大一些。这些特点的战略组合就称为聚点。评论2：在重复博弈中，以往的经历或做法通常就确定了聚点的位置。例如，如果我们第一次分蛋糕，往往彼此可能会同意五五分成。但是，如果曾经按四六分成过，这个比例就为这次划分蛋糕提供了一个聚点。现实生活中聚点的例子：——企业承包分成比例——成行成市——沙滩零售店\n评论3：边界（boundary）是一种特殊的聚点。在边界外的行为存在极度的不确定性。边界一旦确定就具有重要的作用和公共约束力，如共同知识成为一种边界后，就构成行动规则。例如：——在商业领域，两家生产不益于健康的产品的公司可能会达成某种默契，彼此都不在广告中提及各自产品对健康的影响程度。——家庭分工评论4：在没有明确的聚点之前，调解（mediation）和沟通（communication）是十分重要的两种手段。例如：——商业纠纷或家庭财产纠纷中的律师或法庭\n（二）完全信息动态博弈：子博弈精练Nash均衡（subgameperfectNashequilibrium）1.问题的提出（1）如前述，在多个Nash均衡中，究竟哪个均衡会成为最后的均衡？（2）在Nash均衡中，局中人不考虑自己的选择如何影响其他局中人的战略（因为是静态结构）。但在动态结构中，后者会根据前者的行动来调整自己的战略，因此，会考虑自己的选择对其他局中人的影响。（3）由于不考虑自己选择对其他局中人选择的影响，Nash均衡允许存在不可信威胁（在现实中这是不真的）。\n所有动态博弈的核心问题是——可信任性手雷博弈模型第一步：局中人A选择支付1000元给局中人B还是一分不给；第二步：局中人B观察局中人A的选择，然后决定是否引爆一颗手雷将两个人一起炸死。假设局中人B威胁局中人A，如果他不支付1000元就引爆手雷，如果局中人A相信这个威胁，其最优反应是支付1000元；如果局中人A不相信这个威胁，他认为即使给局中人B一个机会，让他将威胁付诸实施，局中人B也不会选择去实施，这样，局中人A就会一分不给。\n2.威胁与威慑不可信与可信威胁设局中人A为潜在市场进入者，局中人B为现有市场的占有者。博弈模型如下：局中人B：占有者接纳竞争进入20，30-10，0局中人A：进入者不进入0，1000，100\n假设：U1为实施威胁的收益U2为不实施威胁的收益可信威胁：U1>U2；不可信威胁：U2>U1例如：——英国农民的故事——母亲对儿子（不做作业）——父亲对女儿（谈恋爱）*威胁与威慑的区别：明确与潜在的进攻或制裁信号。\n3.子博弈精练Nash均衡的概念Selten（1965）通过对动态博弈的分析完善了Nash均衡的概念，并定义了子博弈精练Nash均衡的含义，将Nash均衡中包含不可信威胁的战略剔除出去，使均衡战略不再包含不可信的威胁。这样，就要求局中人的选择在任何时点上都是最优的，局中人需要“随机应变”或“随需而变”，而不能因循守旧。由于剔除了不可信威胁的战略，因而在多数情况下精练Nash均衡缩小了Nash均衡的数量，这对于预测具有重要意义。通俗地说，子博弈（subgame）指包含在一个博弈模型中的一个或若干个阶段博弈。出国读例如：考研本科毕业在国内读就业\n子博弈的定义：子博弈是一个对于所有局中人的信息集而言都是单结的结，这个结的后续结以及在相应的终点结处的支付三个要素所组成的博弈。如果满足下列条件，一个战略组合就是一个子博弈精练Nash均衡（subgameperfectNashequilibrium）：1）它是整个博弈的Nash均衡；2）它的相关行动规则在每个子博弈上都是Nash均衡。评论：一个精练均衡首先必须是一个Nash均衡，但Nash均衡不一定是精练均衡。只有那些剔除了不可信威胁的Nash均衡才是精练Nash均衡。\n序惯理性（sequentialrational）：指一个局中人在博弈的每一个点上都重新优化自己的选择，并且将自己在未来会重新优化其选择这一点纳入到考虑之中。承诺行动（commitment）：指局中人使自己的威胁战略变得可信的行动。通过承诺行动，局中人可以明确地告诉其他局中人其威胁是可信的威胁，而不是不可信的威胁。例如：——企业威胁（宣布降价）——破釜沉舟\n4.应用：房地产开发博弈两个房地产商A和B，他们要作出是否在H市进行开发的决策。他们面临两种市场需求的情况。高需求情况B开发不开发A开发4000，40008000，0不开发0，80000，0低需求情况B开发不开发A开发-3000，-30001000，0不开发0，10000，0\n博弈树的表述：N高低½½AA开发不开发不BBBB开不开不开不开不（4，4）（8，0）（0，8）（0，0）（-3，-3）（1，0）（0，1）（0，0）\n5.Selten连锁店博弈模型假设有一家连锁店（局中人A）在20个城镇中有分店，其编号为1，2，…，20。同时，在每一个城镇都有一个潜在的竞争者，即有一家公司可能通过银行贷款建立同样类型和规模的商店，第k个城镇的潜在竞争者被称为局中人k。这样，就形成了一个局中人A与它的20个潜在竞争者，即局中人k，k=1，…，20之间的一场博弈。如果从传统的博弈论来考虑问题，结论应该是每个潜在竞争者在条件许可下，都会采取“进入”策略，即开设一家与连锁店同类型的商店，而连锁店则应该对新开设的商店采取“接纳”策略，以便取得更多的收益。\n然而，这个结论与实际情况并不符合。几乎所有的人都会认为，连锁店应该对新开设的商店采取“攻击”策略，以保持其垄断地位。另一种方案是连锁店对前面N家商店采取“攻击”策略，而对后20-N家采取“合作”策略。这种方案似乎更符合实际。Selten对这个“连锁店博弈悖论”进行了深入分析，提出了分层次的理性抉择的概念，认为人们对察觉到的理性解决方案，不一定会采取行动。\nSelten连锁店博弈模型的应用：——爱情博弈模型：n个小伙子同时爱上一位姑娘，每个小伙子的占有策略是什么？对于任意局中人i，竞争者均为n-1个。——毛泽东抗日战争与解放战争时期的策略：*抗日战争时期：抗日民族统一战线*解放战争时期：除国民党顽固派之外的所有力量——春秋战国时期：秦国“远交近攻”策略——市场竞争策略\n6.重复博弈（repeatedplay）重复博弈，即是战略依存的厂商（局中人）在长期内相互竞争的状态。在现实中，寡头垄断厂商之间存在重复博弈。重复博弈将改变局中人对博弈的观点，并产生基于长期考虑的新战略，即重复博弈的一种可能结果是产生合作行为。典型的重复博弈包括：——公开串谋（explicitcollusion）——暗中串谋（tacitcollusion）——毛泽东博弈（针锋相对）——中国帝王的激励机制（一人得道，鸡犬升天；一人犯法，株连九族）\n重复博弈应用：军备竞赛（2）假设美苏两国现在还有第三种策略选择：有限军备。这样，双方选择的支付改变为：苏联扩军有限裁军扩军-2000，-2000-1600，-15008000，-∞美国有限-1500，-1600-500，-5009500，-∞裁军-∞，8000-∞，95000，0\n（三）不完全信息静态博弈：贝叶斯Nash均衡（BayesianNashequilibrium）有时，人们将不完全信息博弈称为贝叶斯博弈。在完全信息博弈中，局中人的支付函数是共同知识。在不完全信息博弈中，至少有一个局中人不能确定另一局中人的支付函数。密封报价拍卖、工程招标等都是常见的不完全信息静态博弈的例子。1.不完全信息的市场进入博弈在市场进入博弈中，潜在进入企业决定是否进入一个新市场，但不了解现有企业的成本函数，不了解现有企业决定接纳还是竞争。\n假设现有企业有两种可能的成本函数：高成本和低成本。对应两种成本情况的不同战略组合的支付矩阵如下：现有企业高成本情况低成本情况接纳竞争接纳竞争进入40，50-10，030，80-10，100进入企业不进入0，3000，3000，4000，400在该模型中，进入企业对有关现有企业的成本信息掌握是不完全的，但现有企业了解进入企业的成本函数。如果现有企业是高成本，当进入企业进入时最优选择是接纳；如果是低成本，则最优选择是竞争。在不完全信息条件下，进入企业的最优选择依赖于它在多大程度上认为现有企业是高成本还是低成本。\n假设进入企业认为现有企业是高成本的概率是p，低成本的概率是1-p。进入企业选择进入的期望利润是p（40）+（1-p）（-10），选择不进入的期望利润是0。因此，进入企业的最优选择是：1）如果p大于等于1/5，则进入；2）如果p小于1/5，则不进入（当p=1/5时，进入企业在进入与不进入之间无差异，假定其进入）。评论：在该模型中，进入企业似乎是在与两个不同的现有企业博弈，一个是高成本的现有企业，另外一个是低成本的现有企业。一般地，如果现有企业有T种可能的不同成本函数，进入企业似乎是在与T个不同的现有企业博弈。在1967年以前，博弈论学者认为这样的不完全信息博弈无法分析，因为当一个局中人不了解他在与谁博弈时，博弈的规则是无法确定的。\n2.Bayes博弈模型设博弈中有N个局中人，每个局中人i都有一个行动集Ci，一个可能的类型集Ti，一个概率函数pi以及一个效用函数ui，那么，这就构成了一个Bayes博弈的模型。这种Bayes博弈的典型例子是商业谈判。局中人是买方和卖方，商品对双方都有个底价，但这点并不为对方所掌握。假设商品的价格可能是10元直到100元。如果双方报价，按常规，如果买方的报价高于卖方的报价，那么，他们就在两者的中间价成交；否则，就不成交。于是，这就构成了一个Bayes博弈。\n3.Harsanyi转换1967年，海萨尼（JohnHarsanyi）指出，所有在原来定义下的不完全信息博弈都可以在不改变其本质的前提下被重新模型化为一个完全但不完备的信息博弈。这一切只需要增加一个由自然在不同规则集合中进行选择的初始行动就可以了。在转换后的博弈中，全体局中人都了解新的可变的规则。Harsanyi的思想可以表述为：引入一个虚拟的局中人——“自然”，自然首先行动决定局中人的特征，局中人了解自己的特征，但其他局中人不了解。\nN自然选择不同行动的概率高低[p]进入企业[1-p]不进入进入不进入进入现有企业现有企业（0，300）（0，400）接纳竞争接纳竞争（40，50）（-10，0）（30，80）（-10，100）Harsanyi转换后的市场进入博弈\n4.贝叶斯纳什均衡：求爱博弈假设当有人向你求爱时，你是否接受依赖于对求爱者品德的判断。假设如果你准确知道求爱者品德良好，则选择接受；反之则不接受。但是，你可能并不准确地知道求爱者的品德。这时，你的决策依赖于你在多大程度上相信他是一个品德优良（或恶劣）的人。下面分别是两种情况下的支付矩阵。假设：无论求爱者品德如何，只要他求爱你接受，他就得到100。但你的支付依赖于求爱者的类型，接受一个品德良好的求爱者得100，反之则损失100。求爱者（不论类型如何）在你拒绝时损失50。\n讨论：假设你认为求爱者品德优良的概率为p。求爱者也知道这个p为多少，那么，他求爱你接受时你的预期效用为100p+（-100）（1-p），不接受时的预期效用为零。当p>1/2时，接受才是最优选择。如果p确实大于1/2，贝叶斯（纳什）均衡是：求爱者求爱，你接受。反之，如果p<1/2时，贝叶斯（纳什）均衡为：求爱者不求爱，你不接受。现实生活中的贝叶斯纳什均衡：——赌博——企业招标——拍卖市场（密封报价）\n（四）不完全信息动态博弈：精练贝叶斯均衡（perfectBayesianequilibrium）1.基本概念精练贝叶斯均衡是完全信息动态博弈的精练纳什均衡与不完全信息静态博弈的贝叶斯纳什均衡的结合。一个精练贝叶斯均衡是一个战略组合s和一组信念μ，使得在博弈的每一个结点上都有：（1）给定其他局中人的信念和战略，博弈剩余部分的战略是纳什均衡战略；（2）给定博弈到目前为止的历史，局中人在每一个信息集上的信念都是理性的（这意味着只要有可能，局中人就会根据观察到的行动，通过贝叶斯法则来修正后验概率）。\n2.现实中的精练贝叶斯均衡：——黔驴技穷——买东西时的讨价还价——Spence信号发送模型——企业招聘员工素质错误拒绝正确接受正确拒绝错误接受招聘测试在这里，“成本”成为一个重要的概念，只有负担成本的行动才是可信的。例如：——低成本企业，需要证明——高能力的人、好的员工，需要证明\n小结：四类博弈模型的关键内容：1.完全信息静态博弈。纳什均衡：指由全部局中人的最优战略组成的均衡。例如：囚犯难题。2.完全信息动态博弈。子博弈精练纳什均衡：即局中人的战略在每一个子博弈中都构成Nash均衡，即组成精练Nash均衡的战略必须在每一个子博弈中都是最优的。例如：手雷博弈。3.不完全信息静态博弈。贝叶斯纳什均衡：在给定自己的类型和其他局中人类型的概率分布的情况下，每个局中人的预期效用达到最大化，即没有人有积极性再选择其他战略。例如：求爱博弈。4.不完全信息动态博弈。精练贝叶斯均衡：即局中人根据观察到的其他局中人的行为来修正自己有关后者类型的信念，并由此选择自己的行动。例如：黔驴博弈。\n例题：求博弈的均衡解（7500，0）打击容忍进入不进入中国联通中国移动自然（-10000，-10000）（5000，-10000）（0，10000）\n第三节非线性规划目标值约束其中且\n经济学中的非线性规划方法应用1.消费者选择2.成本最小化3.计划模型消费者效用最大收入>=支出成本最小投入<=资源存量价值最大投入<=资源存量\n本章小结规范研究和实证研究是信息经济学研究的基本方法。信息经济学在经济学的基础上将经典假设完全信息改变为不完全信息，并由此构建的模型与经典均衡理论不同，得到的市场效率机制也就不同。在这一规范研究得出理论的基础上，实证对此作出进一步的检验说明。博弈论是信息经济学的主流研究方法之一依据博弈信息结构的不同，博弈可分为完全信息静态博弈、不完全信息静态博弈、完全信息动态博弈、不完全信息动态博弈四大类，这分别与四类均衡结果相对应。除了运用博弈论的数理推导之外，信息经济学引入了广为经济学界运用的非线性规划理论，以及规范分析、实证分析方法。这些分析都为信息经济学的发展提供了较博弈论更为广阔的研究领域。\n本章要点规范研究的基本假设实证研究的结论讨论博弈的基本要素、类型及其均衡的求解非线性规划的应用模型\n课堂延伸规范研究的学习《“柠檬”市场：质量不确定性与市场机制》趣味博弈：海盗分金币的博弈求解\n推荐阅读文献：1.（美）罗伯特•吉本斯Gibbons：博弈论基础（中译本），中国社会科学出版社，1999年2.张维迎《博弈论与信息经济学》，上海三联书店，1996年3.王则柯，《博弈论平话》，中国经济出版社，1998年4.《博弈生存——社会现象的博弈论解读》，中央编译出版社，2004年5.黄韬等，博弈论的发展与创新，《财经问题研究》，1995年第5期6.刘军跃等，从博弈论看“格兰仕”与“美的”之争，《商业研究》，2002年第5期