统计学讲义(ppt 17页) 16页

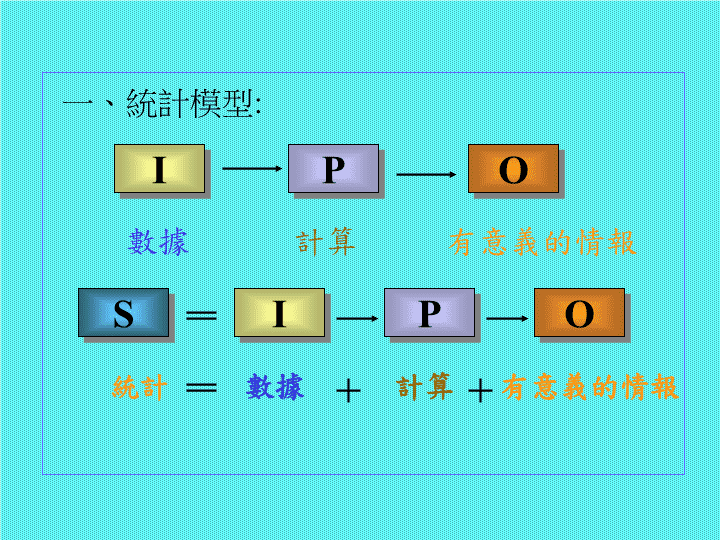
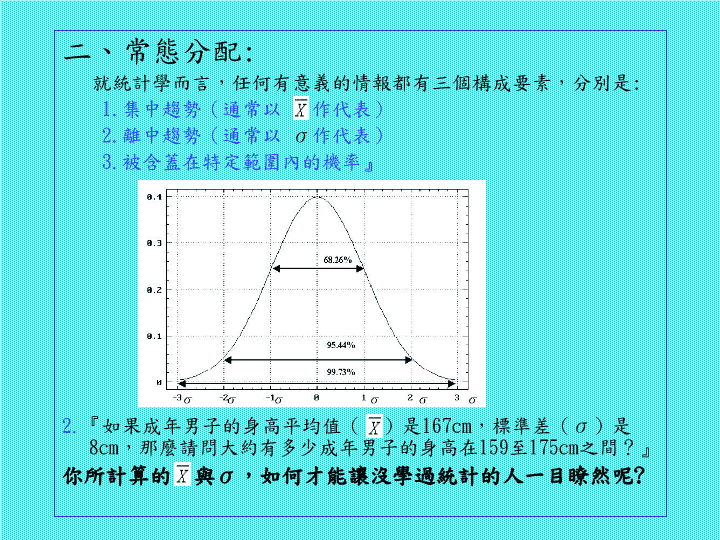
整理—黃明忠先生統計學講義\n一、統計模型:數據計算有意義的情報IPOS統計數據計算有意義的情報IPO\n二、常態分配:就統計學而言，任何有意義的情報都有三個構成要素，分別是:1.集中趨勢（通常以作代表）2.離中趨勢（通常以σ作代表）3.被含蓋在特定範圍內的機率』2.『如果成年男子的身高平均值（）是167cm，標準差（σ）是8cm，那麼請問大約有多少成年男子的身高在159至175cm之間？』你所計算的與σ，如何才能讓沒學過統計的人一目瞭然呢?\n三.直方圖(FrequencyHistogram)傳統做直方圖之前要先斟酌:(1)樣本數，然后依據樣本數來決定(2)分組數，然后再決定(3)每組之組距組界，而后根據上述(1)(2)(3)來設計(4)次數分配表，最后再依據次數分配表來繪制(5)直方圖\n如果我們有一組數據如下：636064626364636266646062616562636663676463626563656162646361那麼依據上述(1)(2)(3)(4)的步驟，我們可以得到它的次數分配表根據這張次數分配表，就可以得到圖(1)的直方圖。──直方圖的目的是什麼？──直方圖可能有那些基本模式？──每一種基本模式透露了那些重要的訊息？──如何運用直方圖來改善品質？組別下組界上組界組中值次數累積次數at orbelow59.5000159.5060.5060.0022260.5061.5061.0035361.5062.5062.00611462.5063.5063.00819563.5064.5064.00524664.5065.5065.00327765.5066.5066.00229866.5067.5067.00130Above67.50=63.1σ=1.72906\n四.不吻合常態分配的基本模式？4.1來源混雜多峰並起圖2A：多峰型直方圖（層別前）多峰型直方圖的原始數據可能是混合了兩個或多個供應商的資料，所以在直方圖研判上，一般應該先用層別法來分析，至於該如何層別呢？\n『如果該層別的直方圖而沒有加以層別，這樣得到的及σ會有意義嗎？』虛胖後的，因此多峰型的直方圖若不先予層別就會造成的虛胖，進而造成管制界限浮濫及製程能力低估等後遺症，因此今後一看到多峰型直方圖請大家切記一定先要──』\n4.2特殊原因形成離島圖3：離島型直方圖離島型直方圖，顧名思義，研判的重點當然要放在離島上，換言之，這一小撮產品不會沒理由的從本島游離出去，把它拉扯出去的力量可能就是統計學所謂的非機遇原因(AssignableCause)，而遇到離島型直方圖就一定要將這些隱藏的特殊原因找出來。』在此情形下要找出真因需要運用專業技術，而非統計邏輯，這也提醒我們診斷問題的統計邏輯與解決問題的專業技術是需要相輔相成的。不過用專業技術找出的原因是否正確，倒可用統計方法來研判，那就是以後要教的統計的檢定。\n4.3偏向一邊洞燭機先圖4：右偏型直方圖『這一類的直方圖既與管理疏失所造成的數據混雜無關(詳見4.1)，又與技術原因造成的離島問題無涉(詳見4.2)。它反而可說是一種難以避免的自然現象，統計學家特別將它稱為偏態型直方圖，換言之它就是會慢慢偏向一邊，請各位想想看，在我們生活週遭，有那些類似的現象？』汽車老了就會愈來愈耗油這一類型的直方圖的確大部分都與老化有關，換言之它反映了某些品質特性的壽命曲線，例如沖模使用久了，沖出來的物件就會愈來愈粗糙，電池使用久了，能量就會逐漸衰減等等，這些現象幾乎無法避免，但是若活用偏態型直方圖卻可將損失降到最小，請各位想一想為什麼？\n五.『統計的推定』(Estimation)『你們知不知道在美國統計專家密度最高的城市是那一個？』為什麼那個鳥不生蛋的地方會吸引一票統計專家呢？『如果能設計一種遊戲讓大家都認為自己很容易贏，那就會吸引一票傻蛋。』『在生管單位決定發料數量時，他們是不是會先賭一下這批產品的良品率？』『有的公司要賭一下產品出廠後的平均使用壽命，以免將來客戶抱怨連連？』這件事不但要賭，而且還要算的非常精確，不然很可能就會大禍臨頭，如何用統計來作預測的問題，這種用統計來作預測的問題，術語就叫做“推定”(Estimation)』。『在統計應用上，推定佔了一席非常重要的地位，尤其像在訂貨生產的公司，如果生管無法推定出報廢率來作發料寬放的依據，那麼不是會造成無效良品的麻煩，就是會搞出數量不足延誤出貨的飛機，前者會造成資金的浪費，後者會引起客戶的抱怨，都很糟糕的事，』\n『請問推定和憑空瞎猜有什麼不同？』根據+嚴謹被推定的未知狀況必須要先根據一些看得見的己知結果而來？任何推定都必須先根據一些樣本的數據來作推衍的基礎例子:某公司希望能預測其產品厚度之範圍，試問應如何下手？及考慮那些因素？假設已量測25個成品，其厚度分別為（單位：mm）：53　48　54　51　4852　46　50　51　4947　55　52　53　4751　50　50　48　5250　48　52　49　47參考此數據在若95%的把握下，請問該公司成品平均厚度在何範圍內?\n『現在我們有了25組數據，那麼請問下一步我們該怎麼辦？』『計算』他們已很清楚的瞭解統計就是數據透過計算產生出有意的情報。『沒錯，此例經過計算之後我們得到=50.12σ=2.403如果您能夠告訴我們95%的產品被含蓋在幾個σ之內，我們就可以推測出它的範圍』\n95%的產品應含蓋在多少個σ之內？』參考此數據在若95%的把握下，請問該公司成品平均厚度在何範圍內？95%產品的平均厚度會落在50.12±1.96x2.403之間\nS統計數據計算有意義的情報IPO六.新I→P→O程序圖(多加上三個空的框框)123推定\n步驟1:隨機抽取樣本步驟2:計算統計量(，σ)步驟3:作出推定結論，下結論時可再細分成兩步驟步驟3A:決定信賴水準(LevelofConfidence,此例為95%)步驟3B:決定信賴區間(Confidenceinterval,此例即為±1.96σ)常用信賴區間與σ個數對照表信賴水準       　含蓋σ個數 　　     信賴區間 　　　90%　　　　　　1.645　　　　　　±1.645σ95%　　　　　　1.96　　　　　　  ±1.96σ99%　　　　　　2.575　　　　　　±2.575σ99.73%　　　　  3　　　　　　　   ±3σ推定最大的危險就是:實際結果與您的推定可能會有很大的出入，\n為什麼會出現這種狀況？1.偏差樣本（BiasedSample）:樣本品質（Quality）隨機抽樣（RandomSampling），不偏樣本（UnbiasedSample），2.與品質相對的樣本數量（Quantity）問題，樣本大時推定比較準？還是樣本小時推定比較準？』推定的精確性（Precision）的確是由樣本大小（n）來決定的，但是我們真的能讓樣本不斷加大嗎？一般如果是用計量值（如上例的厚度）來作推定，那麼最小樣本數不應小於25（n≧25），是一個應該被遵循的遊戲規則。