统计学-计量资料统计描述 50页

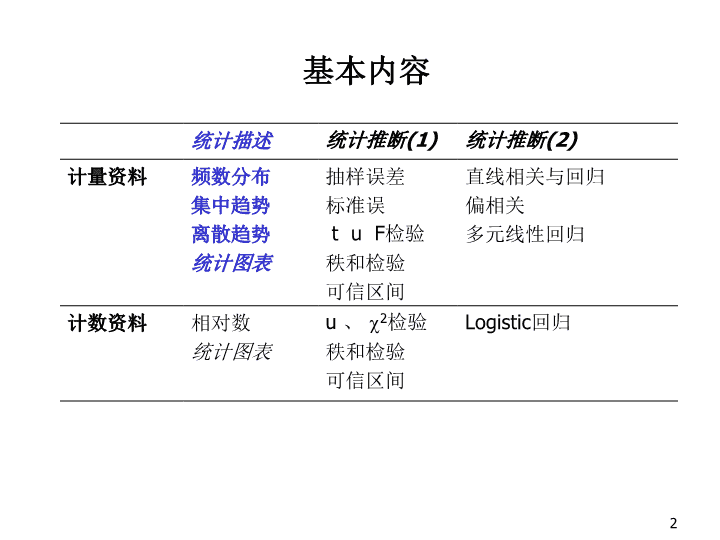
第二章计量资料的统计描述1\n基本内容统计描述统计推断(1)统计推断(2)计量资料频数分布集中趋势离散趋势统计图表抽样误差标准误tuF检验秩和检验可信区间直线相关与回归偏相关多元线性回归计数资料相对数统计图表u、2检验秩和检验可信区间Logistic回归2\n本章在临床资料处理中的用途资料整理阶段，判断资料适合何种方法分析的初步阶段，对变量的特点进行描述（求出均数和标准差）为假设检验做准备3\n为了比较国产药和进口药对治疗更年期妇女骨质疏松效果是否相同，研究人员采取随机双盲的试验方法，对39名病人进行随机分组，国产药组20例，进口药组19例，评价指标为第2-4腰椎骨密度的改变值（骨密度.sav)。1-5.00164.00163.00177.00174.00125.00138.00168.00145.00129.0019.00177.001-2.00189.00177.00163.00170.00136.00182.001-14.002-17.00248.00247.00260.00258.00211.00223.00252.00230.00215.002-4.00如何建立数据库？（注意：在研究的设计和分析阶段都用到统计学）4\n常用的设计类型一组样本与总体的比较两组样本的比较（成组和配对t、2检验）√单因素多组样本的比较（单因素F分析，2检验）√双因素多组样本的比较（配伍组F方差分析）√三因素三组及以上设计（拉丁方设计）三个或以上因素并交互作用（正交设计）5\n主要内容第一节计量资料的频数分布第二节集中趋势第三节离散趋势6\n第一节频数分布什么是频数频数分布的特点频数分布的类型7\n8\nSPSS建立数据库进入SPSS操作窗口进入数据编辑窗口(dataeditor)VariableView变量名类型整数位小数位输入数据:DataView9\n检查输入的数据（打开数据库）找出最大值、最小值（数据排序）dataView窗口－data－sortcases－身高－sortby-身高身高主要集中在什么阶段？（这个程序能否看得出来大多数人身高在何处？应该怎么办？）10\n11\n变量变换：将身高转化成一个新变量（组段）Transform-recode-intodifferentvariables(身高－组段)--change－oldandnew-oldvalue(range)-newvalue(value)-old－new—add—continue（可以试用不同的分组方法，例如“5”“2”）产生新变量（组段）12\n1998年100名18岁健康女大学生身高的频数分布身高组段（1）划记频数f（2）154~112156~11114158~11111，11111，111160~11111，11111，11113162~11111，11111，11111，11111，1122164~11111，11111，11111，111119166~11111，11111，1111115168~11111，11119170~11114172~17411合计10013\n产生频数表Analyze----DescriptiveStatistics----Frequencies－组段－displayfrequencytable14\n频数表计量资料→等级资料15\n16\n频数：当汇总大量的原始数据时，把数据按类型分组，其中每个组的数据个数，称为该组的频数。频数表（频数分布）：表示各组及它们对应的组频数的表格称为频数表或频数分布。（见前两张幻灯）17\n频数分布的两个特征：集中趋势与离散趋势(共性与个性）频数分布的类型：对称分布与偏态分布（集中位置偏向小的一侧叫正偏态，反之叫负偏态）频数表的主要用途：1.揭示分布类型2.发现特大值和特小值3.计算集中趋势指标与离散趋势指标总结前面18\n第二节集中趋势集中位置的描述，即大多数数值落在什么位置上。（针对一个变量的若干个数值）描述集中趋势的几种指标（用不同的方法将不同类型数值的集中位置表示出来）1.算术均数（均数mean）2.几何均数（geometricmean）3.中位数（median）4.众数（Mode）19\n1.算术均数（均数）意义：一组性质相同的观察值在数量上的平均水平。表示（总体）X（样本）（spss:“mean”）应用：正态分布或近似正态分布注意：合理分组，才能求均数，否则没有意义。计算方法：直接法和加权法20\n21\n均数的特征22\n用SPSS计算均数File---Open---Data---身高---Analyze----DescriptiveStatistics----Frequencies----Statistics----Mean---Continue----OK23\n有一组血中抗体滴度数据：32，2，4，8，4，16，1，1，4，1，1，2，2，2，4，8，16，2，4，32，4，8，4,求它们的平均水平24\n首先看这组数据的频数分布，大概集中在什么位置。用“mean”求，看结果如何。File---Open---Data---抗体滴度---Analyze----DescriptiveStatistics----Frequencies----Statistics----Mean---Continue----OK25\n2.几何均数意义：N个数值的乘积开N次方即为这N个数的几何均数。表示：G应用：原始数据分布不对称，经对数转换后呈对称分布的资料。数值范围跨越多个数量级。例如抗体滴度。26\nSPSS计算几何均数File---Open---Data---抗体滴度---Analyze----Reports----CaseSummaries----抗体滴度－Statistics----GeometricMean----Continue---OK27\nCaseSummariesa1.001.001.001.002.002.002.002.002.004.004.004.004.004.004.004.008.008.008.0016.0016.0032.0032.00234.001234567891011121314151617181920212223NGroupedMedianTotal抗体滴度Limitedtofirst100cases.a.28\n1、几何均数适用于对数正态分布，如药物的效价、抗体的滴度、传染性疾病的潜伏期等资料。2、变量x服从对数正态分布，即表示变量lg(xi)服从正态分布。对于lg(xi)，具有正态分布的所有特性。几何均数的特征29\n3.中位数、百份位数意义：将一组观察值从小到大排序后，居于中间位置的那个值或两个中间值的平均值。（身高排队）dataeditor－data－sortcases表示：M、PX百分位数：将N个观察值从小到大依次排列，再分成100等份，对应于X%位的数值即为第X百分位数。中位数是百分位的特殊形式。应用：偏态资料，开口资料30\n11个大鼠存活天数：4，10，7，50，3，15，2，9，13，>60，>60平均存活天数?（一）中位数（median）是将每个变量值从小到大排列，位置居于中间的那个变量值。存活天数2，3，4，7，9，10，13，15，50，>60，>60秩次123456789101131\n计算公式:n为奇数时n为偶数时32\n例9名中学生甲型肝炎的潜伏期分别为12，13，14，14，15，15，15，17,天，求其中位数。1933\n频数表资料的中位数下限值L上限值Ui;fm中位数M34\n偏态资料用算术均数处理会产生什么样的结果？大家试举一个偏态资料的例子。2503128356000150015201600168019202000230023002530258095013000300042103100312032103210410245206812035\n36\nSPSS计算中位数、百分位数File---Open---Data---收入（抗体滴度）----Analyze----DescriptiveStatistics----Frequencies----Statistics----Median（mean）---Continue----OK37\n中位数的特征计算时只利用了位置居中的测量值优点：对极值不敏感缺点：并非考虑到每个观测值适用于各种分布类型的资料，特别适合于：大样本偏态分布资料或者一端或两端无确切数值的资料38\n四、众数（Mode）是一群数据中出现次数（频数）最多的值。适用于大样本；较粗糙。例有16例高血压病人的发病年龄(岁)为：42,45,48,51,52,54,55,55,,61,61,62,62，试求众数。众数的特征1、对于某些数据而言，例如均匀分布，并不存在众数；2、对于某些数据存在两个或多于两个的众数；3、定性数据可以存在众数；众数对于进一步的统计学计算与分析不具备应用价值。58,58,58,5839\n第三节离散趋势描述一组数据参差不齐的程度40\n全距四分位数间距方差标准差变异系数常用指标41\n标准差相关概念：离均差、离均差之和、离均差平方和、方差（2S2）标准差的符号：S（SPSS：Std.deviation）意义：全面反映了一组观察值的变异程度(大小)应用：描述变异程度、计算标准误、计算变异系数、描述正态分布、估计正常值范围42\n用SPSS计算标准差File---Open---Data---身高---Analyze----DescriptiveStatistics----Frequencies----Statistics----Std.deviation---Continue----OK43\n随机变量xi的标准化如果随机变量xi服从正态分布，均数和标准差分别为和s，则随机变量xi的标准化正态离差值（Standardnormaldeviation）又称为标准化得分值（StandardScores）为：44\n变异系数意义：标准差与均数之比用百分数表示。符号:CV计算:CV=（S/X）100%无单位应用：单位不同的多组数据比较均数相差悬殊的多组资料45\n四分位数间距（inter-quartilerange）四分位数间距，用IQR表示：IQR=第三四分位数：Q3第一四分位数：Q146\n多样性指数（IndicesofDiversity）描述无序分类变量在各各义类别间频数的离散度。用熵与最大熵之比表达离散度频率资料的公式频数资料的公式47\n48\n49\n谢谢！50