统计学方差ppt课件 42页

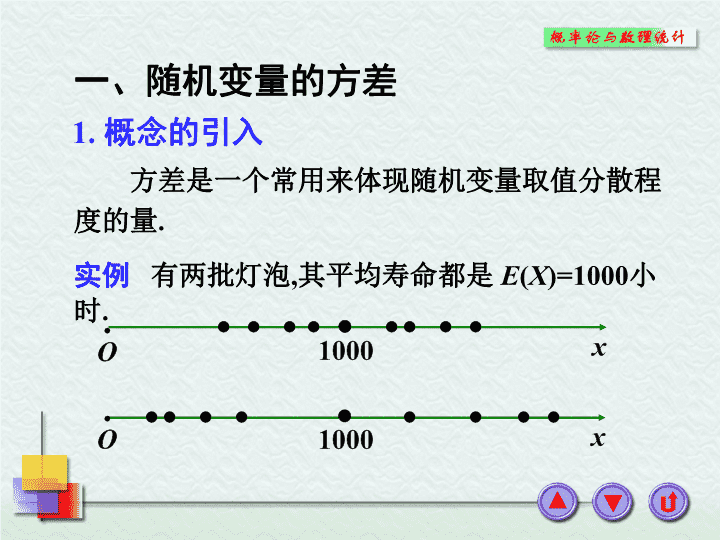
一、随机变量的方差四、例题讲解二、方差的性质五、小结§4.2方　差三、重要概率分布的方差\n1.概念的引入方差是一个常用来体现随机变量取值分散程度的量.实例有两批灯泡,其平均寿命都是E(X)=1000小时.一、随机变量的方差\n2.方差的定义\n方差是一个常用来体现随机变量X取值分散程度的量.如果D(X)值大,表示X取值分散程度大,E(X)的代表性差;而如果D(X)值小,则表示X的取值比较集中,以E(X)作为随机变量的代表性好.3.方差的意义注不能用偏离量X-EX来描述X取值的分散程度,因为其正负偏离相互抵消,即E(X-EX)=0.\n离散型随机变量的方差连续型随机变量的方差4.随机变量方差的计算(1)利用定义计算\n证明(2)利用公式计算注上述公式为计算计算方差的常用公式.\n证明二、方差的性质(1)设C是常数,则有(2)设X是一个随机变量,C是常数,则有证明\n(3)设X,Y相互独立,D(X),D(Y)存在,则证明\n推广\n1.两点分布已知随机变量X的分布律为则有三、重要概率分布的方差\n2.二项分布则有设随机变量X服从参数为n,p二项分布,其分布律为\n\n\n\n3.泊松分布则有\n所以\n4.均匀分布则有\n结论均匀分布的数学期望位于区间的中点.\n5.指数分布则有\n\n6.正态分布则有\n\n\n\n分　　布参数数学期望方差两点分布二项分布泊松分布均匀分布指数分布正态分布\n练习某射手有3发子弹，射击一次命中的概率为0.6，如果命中了就停止射击，否则一直独立地射到子弹用尽。求耗用子弹数X的数学期望和方差.\n练习答案X123P0.60.240.16EX=1.56EX2=3DX=EX2–(EX)2=0.5664\n解四、例题讲解例1\n于是\n解例2\n解例3\n\n解例4\n\n证明取连续型随机变量的情况来证明.切比雪夫不等式切比雪夫切比雪夫不等式\n得\n例题(考研题)1.（2001年数学一，一（5））设随机变量X的方差为2，则根据切比雪夫不等式有估计答案——2.（2001年数学三，一（4））设随机变量X和Y的数学期望分别为-2和2，方差分别为1和4。而相关系数为-0.5，则根据切比雪夫不等式有估计——答案\n练习一1.已知X~B(10,0.2)，Y~N(1,4),且X,Y相互独立,求（1）E(2X-3XY+4X2)；（2）D(X-3Y).答案E(2X-3XY+4X2)=2EX-3EXEY+4EX2=20.4因为EX=2DX=1.6EY=1DY=4,所以D(X-3Y)=DX+9DY=37.6\n练习二2.设随机变量X的方差为2，则根据切比雪夫不等式有估计答案1/2\n五、小结1.方差是一个常用来体现随机变量X取值分散程度的量.如果D(X)值大,表示X取值分散程度大,E(X)的代表性差;而如果D(X)值小,则表示X的取值比较集中,以E(X)作为随机变量的代表性好.2.方差的计算公式\n3.方差的性质4.切比雪夫不等式\nPafnutyChebyshevBorn:16May.1821inOkatovo,RussiaDied:8Dec.1894,inSt.Petersburg,Russia切比雪夫资料