生物统计学9 71页

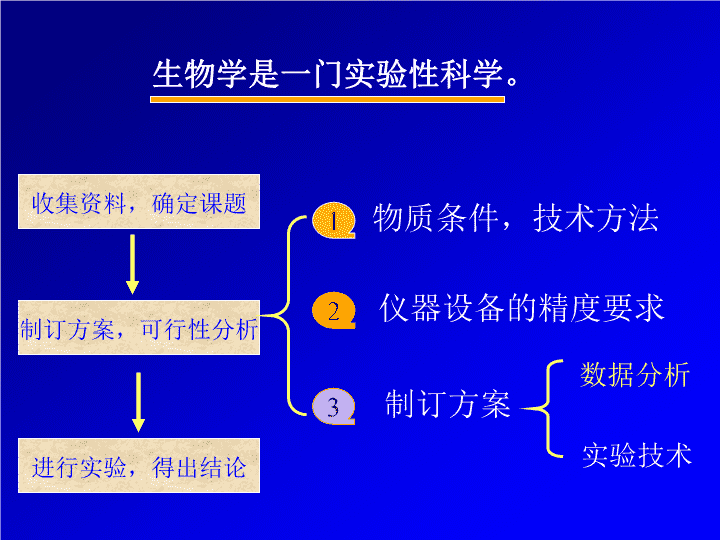
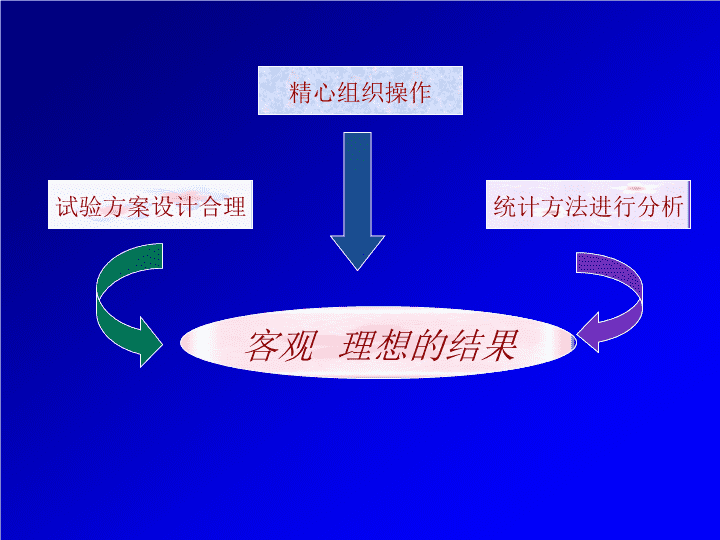
生物学是一门实验性科学。收集资料，确定课题制订方案，可行性分析进行实验，得出结论物质条件，技术方法仪器设备的精度要求制订方案数据分析实验技术123\n试验方案设计合理精心组织操作统计方法进行分析客观理想的结果\n常用试验设计\n田间试验温室试验实验室试验皿内试验人工气候室内试验试验是在人为控制条件下有目的地进行的一种实践活动。\n第一节第二节第三节试验设计的基本原理对比设计随机区组设计常用试验设计及其统计分析第四节第五节裂区设计正交设计\n第一节：试验设计的基本原理一、试验设计的意义二、生物学试验的基本要求三、试验设计的基本要素四、试验误差及其控制途径试验设计(experimentaldesign)五、试验设计的基本原理\n一试验设计的意义(一）概念课题的名称试验目的研究依据、内容试验方案试验单位的选取试验记录项目和要求试验结果的分析方法经济或社会效益分析已备条件尚缺少的条件参加研究人员试验时间、地点成果形式学术论文撰写试验单位的重复数进度安排、经费预算研究的预期效果试验单位的分组试验单位的选取试验单位的重复数试验单位的分组广义狭义\n一试验设计的意义(二）目的避免系统误差，控制、降低试验误差，无偏估计处理效应，从而对样本所在总体作出可靠、正确的推断。\n一试验设计的意义(三）任务在研究工作进行之前，根据研究项目的需要，应用数理原理，作出周密安排，力求用较少的人力、物力和时间，最大限度地获得丰富而可靠的资料，通过分析得出正确的结论，明确回答研究项目所提出的问题。如果设计不合理，不仅达不到试验的目的，甚至导致整个试验的失败。能否合理地进行试验设计，关系到科研工作的成败。\n一试验设计的意义(四）意义节省人力、物力、财力和时间减少试验误差，提高试验的精确度，取得真实的试验资料，为统计分析得出正确的判断和结构打下基础。12\n试验目的明确试验条件要有代表性试验结果可靠试验结果可重演二生物学试验的基本要求\n准确度精确度试验中同一性状的重复观测值彼此接近的程度，即试验误差的大小。试验中某一性状的观测值与其相应真值的接近程度，不易确定。试验结果可靠\n●●●●●既准确又精确●●●●●准确而不精确●●●●●既不准确又不精确●●●●●精确而不准确\n严格要求试验的正确执行和试验条件的代表性；注意试验的环节，全面掌握试验的条件，详实的试验记载考虑季节变异的特点，克服年份、地点环境条件的差异在相同的条件下，再进行试验或实践，应能重复获得与原试验结果相类似的结果。123试验结果重演重演性\n三、试验设计的基本要素基本要素处理因素受试对象处理效应\n处理（因素）概念对受试对象给予的某种外部干预（或措施）特点人为设置单因素处理多因素处理三、试验设计的基本要素\n受试对象处理因素的客体，即根据研究目的而确定的观测总体。必须对其具体条件做出严格规定，保证其同质性。三、试验设计的基本要素\n处理效应处理因素作用于受试对象的反应误差效应试验效应？研究结果的最终体现12三、试验设计的基本要素\n试验误差的概念来源控制途径表示方法四、试验误差及其控制途径\n（一）概念处理的真实效应不能完全一致的其他因素的偶然影响四、试验误差及其控制途径处理效应误差效应试验效应观测值使观测值偏离试验处理真值的偶然影响称为试验误差或误差(error)。\n（一）概念四、试验误差及其控制途径（试验）误差影响试验的精确度和准确度。试验误差是衡量试验精确度的依据，误差小表示精确度高，误差差，则比较的可靠性较差，而要使处理间的差异达到指定的显著水平就很困难。\n系统误差（片面误差）：由于试验处理以外的其他条件明显不一致所产生的带有倾向性的或定向性的偏差。随机误差（偶然误差）：由于试验中许多无法控制的偶然因素所造成的试验结果与真实结果之间产生的误差。人为误差四、试验误差及其控制途径试验误差可以避免不可避免\n试验材料固有的差异试验条件不一致操作技术不一致偶然性因素的影响（二）试验误差的来源四、试验误差及其控制途径\n绝对误差观测值与真值之差相对误差绝对误差与真值之比平均值±标准差（三）试验误差的表示四、试验误差及其控制途径\n保证实验材料的均一性及实验环境的稳定性改进操作管理制度，使之标准化消除系统误差精心选择试验单位采用合理的试验设计（四）试验误差的控制四、试验误差及其控制途径\n重复估计试验误差五试验设计的基本原理重复：试验中同一处理实施在两个或两个以上的试验单位上。如果同一处理只实施在一个试验单位上，那么只能得到一个观测值，则无从看出差异，因而无法估计试验误差的大小。只有当同一处理实施在两个或两个以上的试验单位上，获得两个或两个以上的观测值时，才能估计出试验误差。\n重复降低试验误差五试验设计的基本原理平均数抽样误差的大小与重复次数n的平方根成反比，所以n增加，可以降低试验误差。但在实际应用时，重复数太多，试验材料的初始条件不易控制，也不一定能降低误差。重复数的多少可根据试验的要求和条件而定。\n随机无偏的估计试验误差五试验设计的基本原理随机化是指在对试验材料分组时必须使用随机的方法，使供试材料进入各试验组的机会是相等，以避免试验材料分组时试验人员主观倾向的影响。这是在试验中排除非试验因素干扰的重要手段，目的是为了获得无偏的误差估计量。\n局部控制五试验设计的基本原理局部控制是指在试验时采取一定的技术措施或方法来控制或降低非试验因素对试验结果的影响。在试验中，当试验环境或试验单位差异较大时，仅根据重复和随机化两原则进行设计，不能将试验环境或试验误差所引起的变异从试验误差中分离出来，因而误差较大，试验的精确性与检验的灵敏度降低。\n局部控制降低试验误差五试验设计的基本原理在试验环境或试验单位差异较大的情况下，根据局部控制原则，可将整个试验环境或试验单位分成若干小环境或小组，称为单位组（或区组）。因为单位组之间的差异可在方差分析时从试验误差中分离出来，所以局部控制原则能较好地降低试验误差。\n五试验设计的基本原理重复、随机、局部控制三个基本原则是试验设计中必须遵循的原则，再采用相应的统计分析方法，就能最大程度地降低并无偏估计试验误差，无偏估计处理效应，从而对于各处理间的比较作出可靠的结论。\n随机重复局部控制无偏估计误差降低误差五试验设计的基本原理估计误差统计推断提高精确性三原则作用\n第二节：对比设计对比法：一种最简单的试验设计方法适用于单因素试验。简单对比设计邻比设计只有一个CK每一个处理相邻都有一个CK\n第二节：对比设计6个品系的水稻产量比较实验，设置一个对照品种1CK2CK345CK63CK4CK561CK25CK6CK123CK4每重复的第一个小区安排为处理区，第二个小区安排为CK，以后每隔两个处理区安排一个对照区，同时必须使每一重复的最后一个处理区的一侧有CK。在同一重复内各小区顺序排列，但重复时，使相同小区不要排在一条直线上，可采用阶梯式排列。\n单因素实验常用于少数处理试验及示范性试验，其试验单元排列特点是处理单元直接排列在对照区旁边，使每一小区可与其邻旁的对照区直接比较。\n第二节：对比设计动物试验中称为配对试验设计。把窝别、性别相同、年龄、体重相近的两个动物配成一对，然后用随机的方法将每对的两头动物分别安排到两组中。动物试验中称为配对试验设计。同一对动物之间差异要尽量小些，不同对之间的动物可以有差异。也可进行同一只动物前后两次进行不同的处理，对处理前后的结果进行比较。\n第二节：对比设计对比法试验，由于为顺序排列，不能正确估计出无偏的试验误差，因而试验结果不能采用方差分析的方法进行显著性检验。一般采用百分比法。某处理总和数对邻近CK的％＝邻近CK总和数\n第三节：随机区组设计(randomizedblockdesign)随机区组设计是根据局部控制和随机原理进行的，将试验单位按性质不同分成与重复数一样多的组，使区组内环境差异最小而区组间环境差异最大，每个区组均包括各处理的一个小区。区组内各处理随机排列，各区组独立随机排列。819745623562739184247683951IIIIII肥力高肥力低\n第三节：随机区组设计(randomizedblockdesign)819745623562739184肥力高肥力低247683951IIIIII区组重复随机随机数字法\n第三节：随机区组设计(randomizedblockdesign)随机随机数字法设有8个处理，我们得到随机数字，去掉0，9及重复数字，连续取得8个随机数字，即为一个区组内的排列。9,3,9,4,4,6,0,2,8,4,6,5,9,8,4,4,1,4,9,2,2,4,8,79,3,9,4,4,6,0,2,8,4,6,5,9,8,4,4,1,4,9,2,2,4,8,7\n第三节：随机区组设计(randomizedblockdesign)(1)设计简单，容易掌握(2)富于弹性，单因素、多因素及综合性的试验均可用(3)能提供无偏的误差估计(4)对试验区的形状要求不严\n第三节：随机区组设计(randomizedblockdesign)总平方和自由度区组处理误差A因素B因素互作\n第三节：随机区组设计(randomizedblockdesign)处理数不能太多，一般10个左右。处理数太多，区组必然增大，局部控制的效率降低。处理数或处理组合数不能太少，如果较少，误差项的自由度也会太小，会降低假设检验的灵敏度。\n第四节：裂区设计A1A2A3AaB1B2B3…BbB1B2B3…BbB1B2B3…BbB1B2B3…BbA1A2A3AaB1B2B3…BbB1B2B3…BbB1B2B3…BbB1B2B3…Bb裂区设计是先将每一区按第一因素的处理数划分为小区，称为主区（整区），在主区里随机安排主处理。在主区内引进第二个因素的各个处理（副处理），就是主处理的小区内分设与副处理相等的更小的小区，称为副区（裂区），在副区里随机排列副处理。\n第四节：裂区设计主处理分设在主区，副处理分设于主区内的副区，副区之间比主区之间的试验空间更为接近。在进行统计分析时，可分别估算主区与副区的试验误差，而副区的试验误差小于前者，即副区的比较比主区的比较更为精确。需要考虑\n第四节：裂区设计在一个因素的各处理比另一个因素的各处理需要更大区域时需要较大区域的因素作为主处理，设在主区需要较小区域的因素作为副处理，设在副区应用\n试验中某一因素的主效比另一因素的主效更为重要，而且要求的精度较高将要求精度较高的因素作为副处理，另一因素作为主处理。第四节：裂区设计应用\n根据以往的研究，知道某些因素的效应比另一些因素的效应更大时也适于采用裂区设计将可能表现较大差异的因素作为主处理第四节：裂区设计应用\n试验设计需要临时改动再加入一个试验因素可在原设计中的小区（主区）中再划分小区（副区），增加一个试验因素，就成了裂区设计。第四节：裂区设计应用\n第四节：裂区设计A1A2A3AaB1B2B3…BbB1B2B3…BbB1B2B3…BbB1B2B3…BbA1A2A3AaB1B2B3…BbB1B2B3…BbB1B2B3…BbB1B2B3…BbA因素a个水平B因素b个水平r个区组rab观测值\n主区部分副区部分区组A误差a总变异BA×B误差b总变异r-1a-1(r-1)(a-1)ra-1b-1(a-1)(b-1)a(r-1)(b-1)rab-1变异来源自由度\n对于单因素或两因素试验，因其因素少，试验的设计、实施与分析都比较简单。在实际工作中，常需要同时考察3个或3个以上的试验因素，若进行全面试验，则试验的规模很大，往往因试验条件的限制而难以实施。3因素3水平33＝274因素4水平44＝256\n正交设计正交设计就是安排多因素试验、寻求最优水平组合的一种高效率试验设计方法。在试验的全部处理组合中，仅挑选部分有代表性的水平组合（最优组合）进行试验。通过部分实施了解全面试验情况，从中找出较优的处理组合。特点\n第五节：正交设计正交试验的基本特点：用部分试验来代替全面试验，通过对部分试验结果的分析，了解全面试验的情况。正交试验是用部分试验来代替全面试验，它不可能像全面试验那样对各因素效应、交互作用一一分析;当交互作用存在时，有可能出现交互作用的混杂。虽然正交设计有上述不足，但它能通过部分试验找到最优水平组合，因而适应范围较广。\n3因素3水平33＝27影响某种植物生长有3个因素A因素：营养配方，A1、A2、A3B因素：光照，B1、B2、B3C因素：温度，C1、C2、C3\n第五节：正交设计全面试验可选出最优水平组合分析各因素的效应和交互作用若试验的目的主要是寻求最优水平组合，则可利用正交设计来安排试验。\n在试验安排中，每个因素在研究的范围内选几个水平，如同在选优区内打上网格，如果网上的每个点都做试验，就是全面试验。A2A3A1B1C1B3B2C2C327个\n第五节：正交设计A1B1C1A1B2C2A1B3C3A2B1C2A2B2C3A2B3C1A3B1C3A3B2C1A3B3C29个组合A2A3A1B1C1B3B2C2C3\n一正交表及特点正交表因素的水平数最多可安排的因素（互作）数试验次数（水平组合数）\nABCD1234111112122231333421235223162312731328321393321此表共有4列，可以安排4个因素;每一列有1、2、3三种数字，代表各因素的不同水平;表中有9行，代表9个不同处理组合。\nABCD1234111112122231333421235223162312731328321393321每一列中，不同数字出现的次数相等。任三列中，将同一横行的两个数字看成有序数对时，每一数对出现的次数相等。性质\n均衡分散整齐可比各试验因素的水平值出现次数相等。虽然组合不同，但因素水平是相同的，所以具有可比性。ABCD1234111112122231333421235223162312731328321393321特点\n第五节：正交设计二基本方法确定试验因素和水平数一般不超过四个因素，水平2-4为宜。\n第五节：正交设计二基本方法选用合适的正交表根据试验因素和水平数以及是否需要估计互作来选择合适的正交表。安排下全部试验因素部分试验的水平组合数尽可能少\n第五节：正交设计因素的水平数最少试验次数或处理组合数交互项自由度\n第五节：正交设计4因素BACD2水平ABAC(2-1)*4+1＝5(2-1)*4+(2-1)(2-1)+1＝6\n12345671111111121112222312211224122221152121212621221217221122182212112\n(3-1)*3+1＝7\n\n第五节：正交设计进行表头设计，列出试验方案不要让主效间、主效与交互项间有混杂现象。存在交互作用时，需查交互作用表，将交互作用安排在合适的列上。\n