生物统计学5 116页

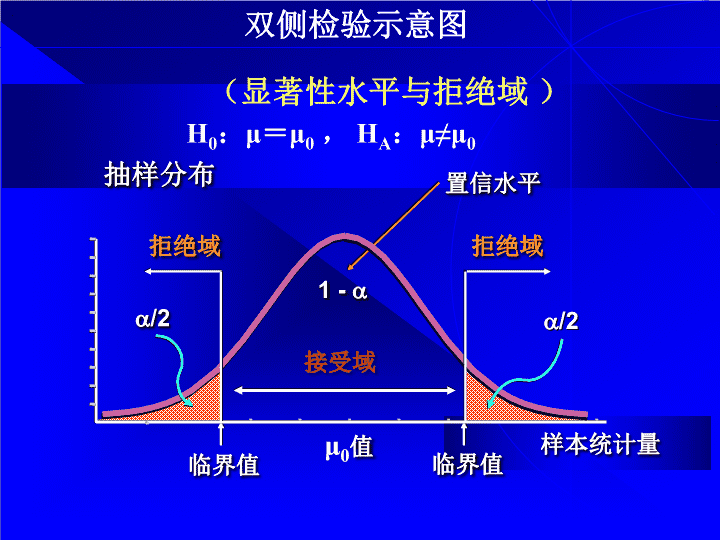
上节重点回顾\n双侧检验示意图（显著性水平与拒绝域）抽样分布μ0值临界值临界值a/2a/2样本统计量拒绝域拒绝域接受域1-置信水平H0：μ＝μ0，HA：μ≠μ0\n\n\n\n假设检验的两类错误根据假设检验做出判断无非下述四种情况：1、原假设真实，并接受原假设，判断正确；2、原假设不真实，且拒绝原假设，判断正确；3、原假设真实，但拒绝原假设，判断错误；4、原假设不真实，却接受原假设，判断错误。假设检验是依据样本提供的信息进行判断，有犯错误的可能。所犯错误有两种类型：第一类错误是原假设H0为真时，检验结果把它当成不真而拒绝了。犯这种错误的概率用α表示，也称作α错误(αerror)或弃真错误。第二类错误是原假设H0不为真时，检验结果把它当成真而接受了。犯这种错误的概率用β表示，也称作β错误(βerror)或取伪错误。\n正确决策和犯错误的概率可以归纳为下表：假设检验中各种可能结果的概率接受H0拒绝H0，接受H1H0为真1-α（正确决策）α（弃真错误）H0为伪β（取伪错误）1-β（正确决策）\n以单侧上限检验为例，设H0：μ≤μ0，H1：μ＞μ0弃真错误区取伪错误区从上图可以看出，如果临界值沿水平方向右移，α将变小而β变大，即若减小α错误，就会增大犯β错误的机会；如果临界值沿水平方向左移，α将变大而β变小，即若减小β错误，也会增大犯α错误的机会。图(a)μ≤μ0H0为真图(b)μ＝μ1＞μ0H0为伪\n错误和错误的关系你不能同时减少两类错误!和的关系就像翘翘板，小就大，大就小在样本容量n一定的情况下，假设检验不能同时做到犯α和β两类错误的概率都很小。若减小α错误，就会增大犯β错误的机会；若减小β错误，也会增大犯α错误的机会。要使α和β同时变小只有增大样本容量。但样本容量增加要受人力、经费、时间等很多因素的限制，无限制增加样本容量就会使抽样调查失去意义。因此假设检验需要慎重考虑对两类错误进行控制的问题。\n两类错误的控制准则假设检验中人们普遍执行同一准则：首先控制弃真错误（α错误）。假设检验的基本法则以α为显著性水平就体现了这一原则。两个理由:统计推断中大家都遵循统一的准则，讨论问题会比较方便。更重要的是:原假设常常是明确的，而备择假设往往是模糊的。如H0：μ＝μ0很清楚，而H1：μ≠μ0则不太清楚，是μ＜μ0还是μ＞μ0？大多少小多少都不清楚。对含义清晰的数量标准进行检验更容易被接受。因此，第一类错误成为控制两类错误的重点。在固定α的条件下，可以考虑如何减小犯β错误的概率。\n用A、B、C、D4种不同N、P配比的营养液浇灌种植的小麦幼苗，30天后计算平均日增重，得到下表的数据，问4种营养液的效果是否相同？营养液日增重（g）A5549624551B6158526870C7165567359D8590767869\n研究单味中药对小鼠细胞免疫机能的影响，把40只小鼠随机均分为4组，每组10只，雌雄各半，用药15d后测定E-玫瑰花环形成率（%），结果如下，试比较各组总体均值之间的差别有无显著性意义？对照组：14  10  12  16  13  14  12  10  13  9党参组：21  24  18  17  22  19  18  23  20  18黄芪组：24  20  22  18  17  21  18  22  19  23淫羊藿组：35  27  23  29  31  40  35  30  28  36\n\n\n第六章方差分析\n方差分析(Analysisofvariance，ANOVA)又叫变量分析，是英国著名统计学家R.A.Fisher于20世纪提出的。它是用以检验两个或多个均数间差异的假设检验方法。\nt检验可以判断两组数据平均数间的差异显著性，而方差分析既可以判断两组又可以判断多组数据平均数之间的差异显著性。有人说，我们可以把多组数据化成n个两组数据（化整为零），用n次t检验来完成这个多组数据差异显著性的判断。到底这种方法行不行\n对多个处理进行平均数差异显著性检验时，采用t检验法的缺点：1.检验过程烦琐。试验包含４个处理t检验：C42＝6次缺点\n缺点2.无统一的试验误差，误差估计的精确性和检验的灵敏性低。t检验：C42＝6次需计算6个标准误误差估计不统一误差估计精确性降低\n缺点3.推断的可靠性低，检验时犯α错误概率大。t检验：C42＝6次H0的概率：1-α＝0.956次检验相互独立6次都接受的概率(0.95)6＝0.735犯α错误的概率＝1-0.735＝0.265犯α错误的概率明显增加例如我们用t检验的方法检验4个样本平均数之间的差异显著性\n试验指标（experimentalindex）：为衡量试验结果的好坏和处理效应的高低，在实验中具体测定的性状或观测的项目称为试验指标。常用的试验指标有：身高、体重、日增重、酶活性、DNA含量等等。试验因素（experimentalfactor）：试验中所研究的影响试验指标的因素叫试验因素。当试验中考察的因素只有一个时，称为单因素试验；若同时研究两个或两个以上因素对试验指标的影响时，则称为两因素或多因素试验。\n因素水平（leveloffactor）:试验因素所处的某种特定状态或数量等级称为因素水平，简称水平。如研究5个温度对酶活力的影响，5个温度就是温度这个试验因素的5个水平。试验处理（treatment）:事先设计好的实施在实验单位上的具体项目就叫试验处理。\n试验单位（experimentalunit）:在实验中能接受不同试验处理的独立的试验载体叫试验单位。一只小白鼠，一条鱼，一定面积的小麦等都可以作为实验单位。重复（repetition）:在实验中，将一个处理实施在两个或两个以上的试验单位上，称为处理有重复；一处理实施的试验单位数称为处理的重复数。\n第一节方差分析的基本原理二、数学模型一、方差分析的基本思想、目的和用途三、平方和与df的分解四、统计假设的显著性检验五、多重比较\n观测值不同的原因处理效应(treatmenteffect)：处理不同引起试验误差：试验过程中偶然性因素的干扰和测量误差所致。方差：又叫均方，是标准差的平方，是表示变异的量。在一个多处理试验中，可以得出一系列不同的观测值。\n方差分析的基本思想总变异处理效应试验误差\n方差分析的目的确定各种原因在总变异中所占的重要程度。处理效应试验误差相差不大，说明试验处理对指标影响不大。相差较大，即处理效应比试验误差大得多，说明试验处理影响是很大的，不可忽视。\n方差分析的用途1.用于多个样本平均数的比较2.分析多个因素间的交互作用3.回归方程的假设检验4.方差的同质性检验1.用于多个样本平均数的比较2.分析多个因素间的交互作用\n二、数学模型假定有k组观测数据，每组有n个观测值，则共有nk个观测值平均T=∑xijTk…Ti…T2T1总和xk1xk2…xkj…xkn………………xi1xi2…xij…xin………………x21x22…x2j…x2nx11x12…x1j…x1n12…j…nk…i…21处理重复xx1x2xixk…\n用线性模型(linearmodel)来描述每一观测值：xij=μ+τi+εij(i=1,2,3…,kj=1,2,3…,n)μ－总体平均数τi－处理效应εij－试验误差xij－是在第i次处理下的第j次观测值要求εij是相互独立的，且服从标准正态分布N(0,σ2)二、数学模型\n对于由样本估计的线性模型为：xij=x+ti+eijx－样本平均数ti－样本处理效应eij－试验误差二、数学模型xij=μ+τi+εij\n根据的τi不同假定，可将数学模型分为以下三种：固定模型随机模型混合模型二、数学模型\n(一)固定模型(fixedmodel)指各个处理的效应值τi是固定值，各个的平均效应τi＝μi－μ是一个常量，且∑τi＝0。就是说除去随机误差以后每个处理所产生的效应是固定的。二、数学模型实验因素的各水平是根据试验目的事先主观选定的而不是随机选定的。\n不同离子对木聚糖酶活性的影响(mg/ml)0.000.250.500.751.001.250.000.060.120.180.240.300.000.400.801.201.602.000.000.400.600.801.001.20固定模型Na+K+Cu2+Mn2+二、数学模型\n在固定模型中，除去随机误差之后的每个处理所产生的效应是固定的，试验重复时会得到相同的结果方差分析所得到的结论只适合于选定的那几个水平，并不能将其结论扩展到未加考虑的其它水平上。固定模型二、数学模型\n(二)随机模型(randommodel)指各处理的效应值τi不是固定的数值，而是由随机因素所引起的效应。这里τi是一个随机变量，是从期望均值为0，方差为σ2的标准正态总体中得到的随机变量。得出的结论可以推广到多个随机因素的所有水平上。二、数学模型\n随机模型美国的黑核桃品种对不同地理条件的适应情况气候、水肥、土壤无法人为控制河南北京广州江苏新疆二、数学模型如果实验条件不能人为控制，那么这个样本对所属总体作出推断就属于随机模型。\n随机模型在随机模型中，水平确定之后其处理所产生的效应并不是固定的，试验重复时也很难得到相同的结果方差分析所得到的结论，可以推广到这个因素的所有水平上二、数学模型\n固定模型与随机模型的比较1.两者在设计思想和统计推断上有明显不同，因此进行方差分析时的公式推导也有所不同。其平方和与df的分解公式没有区别，但在进行统计推断时假设检验构成的统计数是不同的。2.模型分析的侧重点也不完全相同，方差期望值也不一样，固定模型主要侧重于效应值的估计和比较，而随机模型则侧重效应方差的估计和检验3.对于单因素方差分析来说，两者并无多大区别二、数学模型\n(三)混合模型(mixedmodel)指多因素试验中既有固定因素又有随机因素时所用的模型．在实际应用中，固定模型应用最多，随机模型和混合模型相对较少二、数学模型\n三、平方和与df的分解方差是离均差平方和除以自由度的商σ2＝∑(x-μ)2N∑(x-x)2s2=n-1要把一个试验的总变异依据变异来源分为相应的变异，首先要将总平方和和总df分解为各个变异来源的的相应部分。方差分析的基本思想引起观测值出现变异分解为处理效应的变异和试验误差的变异。\n三、平方和与df的分解……平均T=∑xijTk…Ti…T2T1总和xk1xk2…xkj…xkn………………xi1xi2…xij…xin………………x21x22…x2j…x2nx11x12…x1j…x1n12…j…nk…i…21处理重复xx1x2xixk处理间平均数的差异是由处理效应引起的：处理内的变异是由随机误差引起：平方和(x-xi)(xi–x)\n三、平方和与df的分解根据线性可加模型，则有：平方和(xi–x)(x-x)＝(x-xi)+(x-x)2＝[]2(x-xi)+(xi–x)(xi–x)2∑(x-x)2＝∑1n1n(x-xi)2+(x-xi)(xi–x)2∑1n+∑1n每一个处理n个观测值离均差平方和累加：＝(x-xi)2+2(x-xi)(xi–x)+(xi–x)20\n……平均T=∑xijTk…Ti…T2T1总和xk1xk2…xkj…xkn………………xi1xi2…xij…xin………………x21x22…x2j…x2nx11x12…x1j…x1n12…j…nk…i…21处理重复xx1x2xixk(xi–x)＝0(x-xi)2∑1n\n三、平方和与df的分解(xi–x)(x-xi)由于＝0，则：2∑1n∑(x-x)2＝∑(xi–x)2(x-xi)2nn11+∑1n(xi–x)2(x-xi)2(x-x)2＝∑∑1n1k∑∑1n1k+n∑1k总平方和SST处理内或组内平方和SSe处理间或组间平方和SSt平方和把k个处理的离均差平方在累加，得\n三、平方和与df的分解平方和总平方和＝处理间平方和+处理内平方和SST＝SSt+SSeSST＝∑∑(x-x)21n1k=∑x2-T2kn(∑x)2kn＝∑x2-SST＝∑x2-C令矫正数C＝，则：T2kn\n平方和三、平方和与df的分解SSt＝n∑1k(xi–x)2k＝n∑(-2+)1xi2xixx2=n∑-+nk1kxi22n∑1kxxix2=-2nk+n∑1kxi2x2nkx2=-n∑1kxi2nkx2=-n∑1kTi2n2nkT2(nk)2=∑Ti2-Cn1∑1kxi=kxxi=Tin=Tnkx\n三、平方和与df的分解总平方和：SST＝∑x2-C处理间平方和：SSt=∑Ti2-Cn1处理内平方和：SSe=SST-SSt平方和……平均T=∑xijTk…Ti…T2T1总和xk1xk2…xkj…xkn………………xi1xi2…xij…xin………………x21x22…x2j…x2nx11x12…x1j…x1n12…j…nk…i…21处理重复xx1x2xixkT2knC=\n自由度三、平方和与df的分解总自由度也可分解为处理间自由度和处理内自由度：dfT=dft+dfe总df处理间df处理内df\n三、平方和与df的分解自由度dfT=nk-1dft=k-1dfe=dfT-dft=nk-1-(k-1)=nk-k=k(n-1)……平均T=∑xijTk…Ti…T2T1总和xk1xk2…xkj…xkn………………xi1xi2…xij…xin………………x21x22…x2j…x2nx11x12…x1j…x1n12…j…nk…i…21处理重复xx1x2xixk\n三、平方和与df的分解根据各变异部分的平方和和自由度，可求得处理间方差（st2）和处理内方差（se2）：st2=SStdftSSedfese2=\n平方和自由度方差处理间处理内总变异\n用A、B、C、D4种不同N、P配比的营养液浇灌种植的小麦幼苗，30天后计算平均日增重，得到下表的数据，问4种营养液的效果是否相同？=27.227.924.125.830.9T=434.4111.496.2103.2123.6Ti27.030.829.024.622.223.026.724.324.825.726.825.931.924.031.835.91234DCBA营养液重复xixk=4，n=4，nk=16\n例=27.227.924.125.830.9T=434.4111.496.2103.2123.6Ti27.030.829.024.622.223.026.724.324.825.726.825.931.924.031.835.91234DCBA营养液重复xix(1)平方和的计算：T2knC＝＝434.4216＝11793.96SST＝∑x2-C＝31.92+24.02+…+24.62-C＝213.3SSt=∑Ti2-Cn1＝1/4×(123.62+103.22+…+111.42)-C＝103.94SSe＝SST-SSt=213.3-103.94=109.36\n例(2)自由度的计算：dfT＝nk-1=16-1=15dft=k-1=4-1=3dfe=k(n-1)=4×3=12(3)方差计算：st2=SStdft＝103.943＝34.647SSedfese2=＝109.3612＝9.113\n四、统计假设的显著性检验——F检验\n确定各种原因（处理效应、试验误差）在总变异中所占的重要程度。处理间的方差（st2）可以作为处理效应方差的估计量处理内的方差（se2）可以作为试验误差差异的估计量处理效应试验误差方差分析的目的:\n二者相比，如果相差不大，说明不同处理的变异在总变异中所占的位置不重要，也就是不同试验处理对结果影响不大。如果相差较大，也就是处理效应比试验误差大得多，说明试验处理的变异在总变异中占有重要的位置，不同处理对结果的影响很大，不可忽视。处理效应试验误差\nF检验从第三章我们已经知道，从一正态总体（μ,σ2）中随机抽取两个样本，其样本方差s12与s22的比值为F：F＝s12s22其F分布曲线随着df1和df2的变化而变化。由于F值表是一尾的（F值的区间〔0，+∞)），一般将大方差作分子，小方差作分母，使F值大于1，因此，表上df1的代表大方差自由度，df2代表小方差自由度。\n用处理效应的方差（st2）和实验误差的方差（se2）比较时，我们所做的无效假设是假设处理效应的变量和实验误差的变量是来自同一正态总体的两个样本，因此处理效应的方差（st2）和实验误差的方差（se2）的比值就是F值，即处理效应试验误差=方差分析\nF检验在进行不同处理差异显著性的F检验时，一般是把处理间方差作为分子，称为大方差，误差方差作为分母，称为小方差。无效假设是把各个处理的变量假设来自同一总体，即处理间方差不存在处理效应，只有误差的影响，因而处理间的样本方差σt2与误差的样本方差σe2相等：Ho：σt2＝σe2HA：σt2≠σe2\nF检验与t检验相类似，F检验是把计算所得的F值与临界Fα值比较，判断由误差造成的概率大小，最后作出统计推断。无效假设是否成立，要看计算的F值在F分布中出现的概率。\nF＜F0.05P＞0.05处理间差异不显著F＞F0.05P＜0.05处理间差异显著F＞F0.01P＜0.01处理间差异极显著否定Ho否定Ho接受Ho我们确定显著标准水平α后，从F值表中查出在dft和dfe下的Fα值\n综上所述，可归纳成方差分析表(analysisofvariancetable)se2k(n-1)SSe误差或处理内nk-1SST总和st2k-1SSt处理间F均方自由度平方和变异来源F＝st2se2F检验\n上例中，4个不同营养液处理小麦的增重的F值为：F＝st2se2＝34.6479.113＝3.802dft＝3dfe＝12，查F值表得F0.05＝3.49，F0.01＝5.95不同营养液处理的小麦的增重量差异是显著的例F0.01>F>F0.050.01F0.01，P<0.01，说明5个地区黄鼬冬季针毛长度差异极显著。\n结果做成方差分析表：不同地区黄鼬冬季针毛长度方差分析表变异来源SSdfs2FF0.05F0.01地区间地区内173.7112.9941543.430.8750.15**3.064.89总变异186.7019为了确定各个地区之间的差异是否显著，需要进行多重比较。\n这里用最小显著差数法（LSD）进行检验。查t值表，当dfe=15时，t0.05＝2.131，t0.01＝2.947，于是有：LSD0.05=2.131×0.658=1.402LSD0.01=2.947×0.658=1.939本例中各组内观测数相等，而且组内方差均为0.866，故任何两组的比较均可用LSD0.05及LSD0.01。\n在进行LSD0.05及LSD0.01比较时，各组间差数>LSD0.01，说明两地间差异极显著，标以不同的大写字母；LSD0.01>各组间差数>LSD0.05，说明两地间差异显著，标以不同的小写字母；\n地区平均数差异显著性α＝0.05α＝0.01东北内蒙古河北安徽贵州31.6027.4026.0324.7522.85abbccdABBCCDD结果表明，东北与其它地区，内蒙古与安徽、贵州，河北与贵州黄鼬冬季针毛长度差异均达到极显著水平，安徽与贵州差异达到显著水平，而内蒙古与河北、河北与安徽差异不显著。\n根据组内观测次数目不同组内观测次数相等的方差分析组内观测次数不相等的方差分析\n有时由于试验条件的限制，不同处理的观测次数不同，k个处理的观测次数依次是n1、n2、…、nk的单因素分组资料，前面介绍的方差分析方法仍然可用，但由于总观测次数不是nk，而是次，在计算平方和时公式稍有改变。组内观测次数不相等的方差分析se2∑ni-1SSe误差或处理内SST总和st2k-1处理间F方差自由度平方和变异来源F＝st2se2∑ni-k\n在作多重比较时，首先应计算平均数的标准误。由于各组内观测次数不等，因此应需先算得各ni的平均数n0：各个处理的样本容量用于LSR检验用于LSD检验\n用某种小麦种子进行切胚乳试验，实验分为三种处理：整粒小麦（I），切去一半胚乳（II），切去全部胚乳（III），同期播种与条件较一致的花盆内，出苗后每盆选留两株，成熟后进行单株考种，每株粒重结果如表，试进行方差分析。处理株号合计平均数12345678910ⅠⅡIII21202429252224252822232525292130312627242626202120424414625.524.424.3小麦切胚乳试验单株粒重（g）\n处理株号合计平均数12345678910ⅠⅡIII21202429252224252822232525292130312627242626202120424414625.524.424.3小麦切胚乳试验单株粒重（g）n1＝8，n2＝10，n3＝6，N＝24(1)平方和的计算\nSST＝∑x2–C=212+292+…+262-C=230.5SSe＝SST-SSt＝230.5-6.8＝223.7(2)自由度的计算\n(3)列方差分析表变异来源SSdfs2F处理间处理内6.8233.72213.410.70.318总变异230.523由表中结果可知，F＜1，表明三种处理的每株粒重无显著差异。\n由于F检验不显著，不需要再作多重比较。如果F检验显著，则需要进一步计算n0，并求得（用于LSR检验）或（用于LSD检验），即x1x2-SxS\n需要指出的是，不等观测次数的试验要尽量避免，因为这样的试验数据不仅计算麻烦，而且也降低了分析的灵敏度。