统计学基础知识 7页

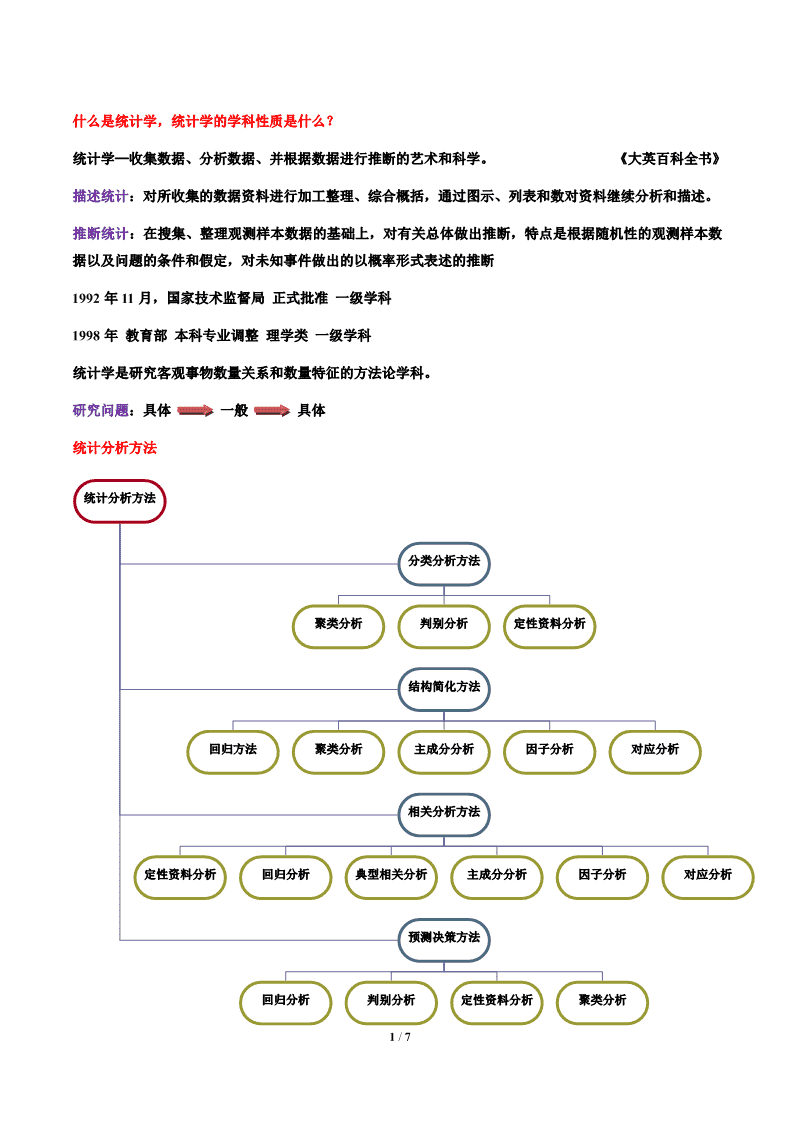
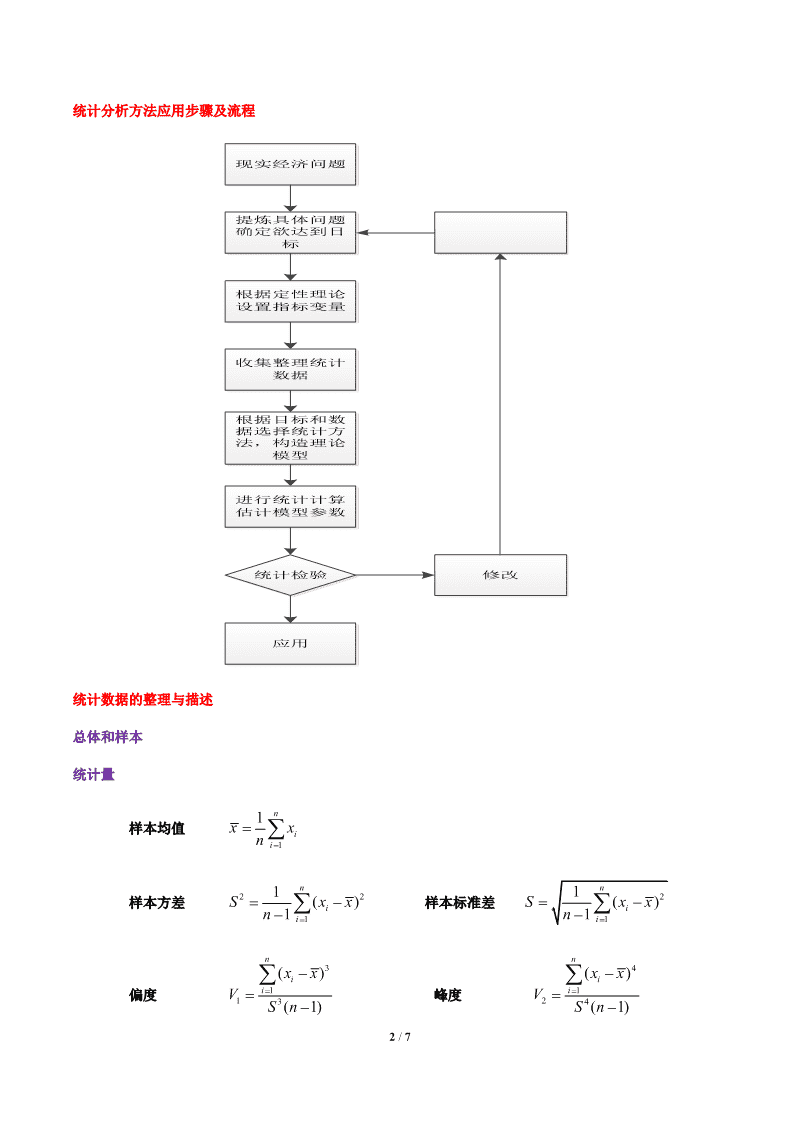
什么是统计学，统计学的学科性质是什么？统计学—收集数据、分析数据、并根据数据进行推断的艺术和科学。《大英百科全书》描述统计：对所收集的数据资料进行加工整理、综合概括，通过图示、列表和数对资料继续分析和描述。推断统计：在搜集、整理观测样本数据的基础上，对有关总体做出推断，特点是根据随机性的观测样本数据以及问题的条件和假定，对未知事件做出的以概率形式表述的推断1992年11月，国家技术监督局正式批准一级学科1998年教育部本科专业调整理学类一级学科统计学是研究客观事物数量关系和数量特征的方法论学科。研究问题：具体一般具体统计分析方法统计分析方法分类分析方法聚类分析判别分析定性资料分析结构简化方法回归方法聚类分析主成分分析因子分析对应分析相关分析方法定性资料分析回归分析典型相关分析主成分分析因子分析对应分析预测决策方法回归分析判别分析定性资料分析聚类分析1/7\n统计分析方法应用步骤及流程现实经济问题提炼具体问题确定欲达到目标根据定性理论设置指标变量收集整理统计数据根据目标和数据选择统计方法，构造理论模型进行统计计算估计模型参数统计检验修改应用统计数据的整理与描述总体和样本统计量n1样本均值xxini1nn22112样本方差S()xix样本标准差S()xixn1i1n1i1nn34()xxi()xxii1i1偏度V峰度V1324Sn(1)Sn(1)2/7\n几种重要的概率分布正态分布2分布t分布F分布自由度估计点估计区间估计最小二乘估计极大似然估计矩估计假设检验的原理与步骤在假设检验中,我们要依据样本数据做出接受或拒绝H0(原假设)的选择.那么做出这种选择的理论根据是什么呢?我们指出,假设检验的理论根据是“小概率事件的实际不可能原理”,即概率很小的随机事件在个别试验中几乎是不可能发生的.下图给出了假设检验的原理。由假设检验的原理可见，假设检验真正有意义的工作是在拒绝原假设时。假设检验的一般步骤:1)根据实际问题提出原假设和备择假设;3/7\n2)给出显著性水平;3)确定合适的检验统计量;4)在认为原假设为真的前提下,构造一个与检验统计量有关的小概率事件A,即确定A,使得P(A|H为真）;0求出H0的拒绝域,即事件A发生时,上述统计量的取值范围.H0的拒绝域也称为假设检验的拒绝域.根据样本观察值,求出统计量的观察值,从而确定是否接受H0.(统计量的观察值落在拒绝域内,则拒绝H0;反之,接受H0).多元分布的基本概念方阵的特征值（根）与特征向量设A为一n阶方阵。如果存在数和非零的n维向量X，使得AXX成立，则称为方阵A的特征值，X为A的对应于特征值的特征向量。例1矩阵.xls(sheet1)正交矩阵如果n阶方阵A满足AAI，则称A为正交阵。A为正交阵的充分必要条件是A的列向量都是单位向量，且两两正交。例1矩阵.xls(sheet2)正定矩阵设A为一n阶方阵。如果对任意非零的n维向量X，都有XAX0成立，则称A为一正定矩阵。半正定矩阵（定义）n阶半正定矩阵一定有n个非负的特征根（包括重根）。随机向量及其分布随机变量就是以不同的可能性（概率）进行取值的变量。如：在抽检产品时，引入随机变量X，使正品对应X=1,次品对应X=0;4/7\n掷硬币时，引入随机变量X,使正面对应X=1,反面对应X=0;掷骰子时，引入随机变量Y,其取值范围为1，2，3，4，5，6，使Y的每一个取值对应于一种抛掷结果；检测白糖重量时，引入随机变量Z,其取值范围为490—510，使每一检测结果都可由Z的一个取值表示。随机变量可分为离散型和连续型两种。离散型随机变量的全部取值可一一列举（试验结果有有限种或可列种，如某服务台前等待服务的顾客数），连续型随机变量可连续取值（对应于在一个区间内取值的情况，如电子元件的寿命，测量误差等）。随机向量：每个分量都是随机变量的向量。随机向量的期望与协方差矩阵设X(x1,x2,,xn)是一个随机向量，则称E(X)(E(x),E(x),,E(x))12n为随机向量X(x1,x2,,xn)的期望。对两个随机向量X(x1,x2,,xn)，Y(y1,y2,,ym)，称矩阵cov(x1,y1)cov(x1,y2)cov(x1,ym)cov(x2,y1)cov(x2,y2)cov(x2,ym)cov(X,Y)为这两个随机向量的协方差矩阵，其中cov(x,y)cov(x,y)cov(x,y)n1n2nmcov(x,y)E[(xE(x)][yE(y)]。ijiijj特别地，称cov(X,X)为X的协方差矩阵，简记为V(X)。称矩阵(x1,y1)(x1,y2)(x1,ym)(x2,y1)(x2,y2)(x2,ym)(X,Y)(x,y)(x,y)(x,y)n1n2nm为这两个随机向量的相关矩阵，其中(xi,yj)为随机变量xi和yj的相关系数，5/7\ncov(x,y)ij(x,y)。ijD(x)D(y)ij特别地，称(X,X)为X的相关矩阵。通常，我们将一个随机向量的协方差矩阵记为(ij)、相关矩阵记为R(ij).任何随机向量的协方差矩阵（相关矩阵）都是半正定矩阵。任何随机向量的n阶协方差矩阵（相关矩阵）都有n个非负的特征根（包括重根）和n个相互正交的单位特征向量。多元正态分布如果随机变量X的概率密度函数为2(x)12f(x)e2,x,222则称X服从参数为,的正态分布，记为X～N(,).特别地N(0,1)称为标准正态分布。正态随机变量的概率密度函数f(x)具有如下性质：1．图形呈钟型，以x为对称轴；22．在x处，f(x)取最大值。x值离越远，f(x)值越小，且以x轴为渐近线。越小，曲线2越陡峭；越大，曲线越平缓。2．密度曲线与x轴围成的面积恒等于1.23．E(X),D(X)6/7\n设p维随机向量X(x1,x2,,xp)的联合概率密度函数为111f(x)p/21/2exp[(x)(x)]，(2)||2其中为p维实向量，为p阶正定矩阵，则称X服从p元正态分布，也称X为p维正态随机变量，简记为X～N(,).此时，E(X),V(X)7/7