- 680.00 KB
- 2022-09-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
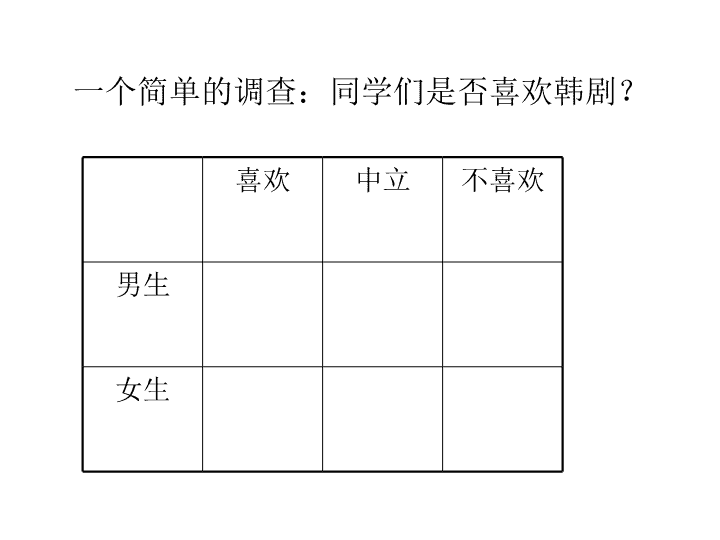
第一讲教育与心理统计学概述\n一个简单的调查:同学们是否喜欢韩剧?喜欢中立不喜欢男生女生\n\n\n初步核算,前三季度国内生产总值166043亿元,同比增长11.5%,比上年同期加快0.7个百分点。其中,一季度增长11.1%,二季度增长11.9%,三季度增长11.5%。分产业看,第一产业增加值18207亿元,增长4.3%,回落0.6个百分点;第二产业增加值83478亿元,增长13.5%,加快0.2个百分点;第三产业增加值64358亿元,增长11.0%,加快1.5个百分点。[2007-10-2510:12:16]\n2007年各月份CPI涨幅12月6.50% 11月6.90%10月6.50% 9月6.20%8月6.50% 7月5.60%6月4.40% 5月3.40%4月3.00% 3月3.30%2月2.70% 1月2.20%\n例题:王老师是一位心理学教师,本学期期末所教班级的学生考试成绩如下:81,73,64,59,94,82,67,75,90,48,57,86,75,93,88,72,65,77,60,79,70,81,56,64,73,99,87,66,50,45,80,82,67,74,68,92,54,57,87,64,76,55,61,65,70,89,71,49,60,72,70,83,67,74。问题:王老师应该怎样比较全面地整理出这次考试分数?怎样初步评价这次考试结果?\n检测项目结果参考标准考试人数:20平均分数:76.100成绩标准差:4.047-10考试优良率%20.00%考试合格率%100.0%最高分:84.0最低分:66.0考试信度:->0.7考试效度:0.6162>0.4成绩分布正态性检验:成绩分布服从正态分布服从正态分布偏度:-0.3786峰度:-0.3594试卷总体难度:0.7605试卷总体区分度:0.1000>0.2心理学考试质量分析表\n你在一本心理杂志上看到这样一段文字:“独立组的t检验表明,在训练之前,实验组与控制组之间,在三个方面无显著差异,三个t值分别是t(18)=0.39,P>0.05;t(18)=0.14,P>0.05;t(18)=1.35,P>0.05。”心理与教育测量、实验心理学你如何理解下面的实验结果?\n关于统计的初步理解1、数据;2、统计图表;3、统计指标;4、数据的搜集、获取方法:问卷调查、实验、测量、观察等\n第一节统计方法在心理和教育科学研究中的作用一、心理与教育统计的定义与性质二、心理与教育科学研究数据的特点三、学习心理与教育应该注意的事项\n一、心理与教育统计的定义与性质(一)定义心理与教育统计学是专门研究如何运用统计学原理与方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育活动规律的一门科学。1.统计学原理:2.随机性数据3.数据搜集获取方法:问卷调查、实验、测量、观察等4.数据分析处理方法:绘制图表;计算统计量——主要包括描述性统计量和推断性统计量、实验设计;分析5.得出结论:该结论可以普遍适应于所有情境\n(二)统计学的分类(1)理论统计学(2)应用统计学(3)两者的关系(三)心理与教育统计的性质(1)应用统计学学:着重研究介绍各种统计方法在不同的心理与教育研究中应用的条件和具体方法,及其统计计算结果的解释。(2)量化研究\n运用……研究……数量关系的学科统计学应用统计心理与教育统计学人口统计学经济统计学生物统计学……教育与心理统计学的性质数理统计原理与方法\n二、心理与教育科学研究数据的特点(一)心理与教育科学研究的数据与结果多用数字形式呈现(二)心理与教育科学研究数据具有随机性和变异性1.定义:科学研究中因观测人员、观测工具、观测条件的变化而具有随机变化的显像。2.随机因素:造成数据变异的原因,出自观测过程中一些偶然的不可控制的因素3.随机误差:4.随机误差的原因\n(三)心理与教育科学研究数据具有规律性1.变量2.一次结果的随机性3.多次结果的规律性(四)心理与教育科学研究的目标是通过部分数据来推测总体特征1.统计研究的目的:研究总体而非个别事件2.统计研究对象:研究有一定代表性的部分对象,最终通过样本研究对总体做出有效可靠的推论\n三、学习心理与教育应该注意的事项(一)要注意的几个问题1.必须克服畏难情绪2.重点掌握各种统计方法使用的条件3.加强课后练习(二)要切记的一些要点1.克服“统计无用”与“统计万能”的思想,注意科研道德2.正确选用统计方法,防止无用和乱用统计(1)分析一下实验设计是否合理(2)分析实验数据的类型(3)分析数据的分布规律\n第二节心理与教育统计学的内容一、描述统计二、推断统计三、实验设计四、教育研究中的三者之间关系五、心理与教育统计研究的分类\n一、描述统计(一)描述统计的定义描述统计(descriptivestatistics):主要研究如何整理心理与教育科学实验或调查得来的大量数据,描述一组数据的全貌,表达一件事物的性质。1.数据分组与统计图表2.数据分布状态3.集中量数:4.差异量数:5.地位量数6.相关量数:\n(二)描述统计的作用1.可以描述局部的、一组数据的情况;也可以描述整体数据的情况2.使杂乱无章的数据更好地呈现出显示事物的特征与变化趋势\n二、推断统计(一)推断统计的定义推断统计(inferentialstatistics):主要研究如何通过局部数据所提供的信息,推论总体的情形。1.总体参数(特征)值的估计2.各种各样的假设检验3.各种非参数的统计方法\n推论统计:根据已获得的样本数据所提供的信息来推论总体的特征的统计方法。通常包括总体参数估计和假设检验(t、Z、F、2检验等)两部分。\n总体而言,推荐生与统考生的身心发展状况分别如何?(参数估计)推荐生身心发展是否显著好于统考生?(假设检验)\n(二)推断统计的理论基础1.抽样理论及其方法:在什么情况下可以从样本的特性推论出总体的特性;其中,最重要的是样本抽取的“随机性”原则2.估计理论及其方法:主要是根据随机抽样的结果来估计总体分布的参数值,分为点估计和区间估计3.统计检验及其方法:根据实际的抽样结果来推论有关总体特征的假设是否与具体的随机抽样所提供的信息相一致。\n(三)推断统计的作用1.从局部数据估计总体的情况2.对假设进行检验与估计3.对影响变化的因素进行分析4.对两件事物或多件事物之间的差异进行比较\n三、实验设计(一)实验设计的定义实验设计(experimentaldesign):主要目的在于研究如何科学地、经济地以及更加有效地进行实验。一项严谨的实验研究,在实验前就要对研究的基本步骤、取样方法、实验条件控制、实验结果数据的统计分析。通常包括研究课题的确定、研究变量的确定、研究对象的抽取、研究方法、研究工具、研究结果的统计分析方法的选择等。\n选择哪些方面作为衡量学生发展的指标(学习成绩、心理健康水平、身体素质、解决问题能力等)?(研究变量的确定)选择多少学生?(样本容量的确定)怎样选取学生?(抽样方法的选择)用什么统计方法进行分析?(统计方法的选择)假如你在某个小学任校长,该校正在进行一项教学改革,如何评价改革的成败?\n推论统计可靠数据一般水平及关系样本↓总体描述统计实验设计(保障)概率分布平均(基础)(核心)推论统计推论统计(核心)四、教育研究中的三者之间关系\n五、心理与教育统计研究的分类依据研究的问题实质,主要可以分为:1.描述一件事物的性质2.比较两件事物之间的差异3.分析影响事物变化的因素4.一件事物两种不同属性之间的相互关系5.取样方法\n第三节心理与教育统计学的发展一、统计学的发展历程二、统计在心理与教育研究中的应用三、心理与教育统计在中国的发展与应用\n一、统计学的发展历程(一)统计学的形成1.古代作为“政治算术”的统计工作统计工作最初是为统治者治理国家的需要而组织的收集资料的工作(1)古埃及时期的全国人口与财产调查(2)古希腊及罗马时期的人口调查与财产登记(3)中国大禹治水时期的分配贡赋制度\n2.“统计学”的出现(1)拉丁文“status”:对各种现象和基本情况进行简单的估量(2)意大利文“stato”:国家概念,国家机构与国力的总和。此时“stato”的概念与“计量”只有隐含的联系(3)18世纪的德文“statistika”:正式命名为“统计学”,意为国家应该注意的事实学问,包括国家的组织、人口、军队、国民职业和地上地下资源。但是,此时的“统计”多用文字表述,极少用数字(4)英国数学家配第的“statistics”:专门研究各种数量,数字是它的专用形式(5)当前的“统计学”概念的理解:一是指该门学科本身,指它的知识总体;二是指许多统计测量值组成的一个集合;三是指统计技术或统计量\n(二)统计学的理论基础——概率论与正态分布曲线方程的产生1.概率论的创立(1)16世纪的伽利略对概率论的提出(2)17世纪的帕斯卡和费马的概率论的创立2.正态分布曲线方程(1)17世纪末18世纪初贝努里:贝努里定理为发现正态概率分布创造了条件(2)1733年隶莫夫提出了正态分布概率和概率的乘法运算法则,推导出正态曲线方程(3)18世纪的高斯和拉普拉斯各自独立发现正态曲线分布方程,高斯还首次提出了正态分布曲线(4)19世纪的泊松提出了“大数定理”\n(三)数理统计的产生与发展——描述统计学与推论统计学1.“数理统计”的提出(1)19世纪的凯特勒:首先提出要将统计学与数学中的概率论结合,以概率论为理论基础确立统计研究方法(2)1867年韦特斯坦:首次提出“数理统计”,后又发展为数理统计学派2.描述统计学:以高尔顿和皮尔逊为代表(1)高尔顿:中位数、百分位数、四分差、相关与回归概念及其计算方法(2)皮尔逊:频率曲线理论、直线相关系数及其计算方法、配合度检验方法、大样本理论(3)格塞特:小样本理论、t分布3.推论统计学:以费舍为代表(1)费舍:论证t分布、F分布理论、实验设计、随机化、点估计与区间估计理论(2)二战后:非参数法、序列分析、随机过程研究、小样本分布、多元统计理论与方法\n二、统计在心理与教育研究中的应用(一)心理与教育统计与数理统计的关系1.数理统计原理及其方法在心理研究、教育研究中的应用:正态分布理论等2.心理与教育统计对统计学的推动:因子分析等(二)数理统计在心理与教育研究中的应用(1)凯特勒:提出身高、体重等非常近似地遵循正态分布曲线(2)高尔顿:高斯的误差理论推广到人类行为的测量中,首创回归理论(3)皮尔逊:皮尔逊相关系数、X2分布及其检验(4)斯皮尔曼:等级相关系数、因子分析(5)20世纪后贡献较大的是:卡特尔、桑代克、瑟斯顿等\n三、心理与教育统计在中国的
发展与应用(一)20世纪20年代后关于心理与教育统计方面的译著和专著的出版发行,以及统计思想与技术的介绍、传播、普及(二)20世纪50年代后心理学受挫,严重影响了我国心理与教育科学研究的开展与提高(三)20世纪80年代初期心理学新生,心理与教育统计学也开始复苏(四)20世纪90年代末期紧密结合计算机科学的发展、紧随该学科国际发展前沿动态\n第四节心理与教育统计的基础概念一、数据类型二、变量、观测值、随机变量三、总体、样本与个体四、次数、比率、频率与概率五、参数和统计量\n一、数据类型(一)从数据的观测方法与来源分析1.计数数据(countdata):计算个数的数据2.测量数据(measurementdata):借助于一定的测量工具或一定的测量标准而获得的数据。\n(二)从数据反映的测量水平来分1.称名数据(nominaldata):只说明某一事物与其它事物在属性上的不同或类别上的差异它具有独立的分类单位,其数值一般都取整数形式,只计算个数,并不说明事物之间差异的大小。有关被试属性的调查资料,大多属于这类数据。2.顺序数据(ordinaldata):是指既无性等单位,也无绝对零点的数据,是按事物某种属性的多少或大小,按次序将各个事物加以排列后获得的数据资料。3.等距数据(intervaldata):是具有相等单位,但无绝对零点的数据4.比率数据(ratiodata):能表明量的大小,既有相等单位,同时也具有绝对零点。\n(三)从数据是否具有连续性来分1.离散数据(discretedata):又称不连续数据,该类数据在任何两个数据点之间所取的数值的个数是有限的,如从事某一职业的人数、球赛比分、班级个数等。2.连续数据(continuousdata):指任意两个数据点之间都可以分出无限多个大小不等的数值,如年龄、长度、重量、自信心等。\n(四)不同类型数据之间的关系\n二、变量、观测值、随机变量(一)变量1.变量(variable):就是指心理与教育实验、观察、调查中想要获得的数据,即为一个可以取不同数值的物体属性或事件,其数值具有不确定性。2.常数(constant):在一定范围内其数值不会改变(二)观测值和个案1.观察值(observation):一旦确定了某个数值,就称该数值为变量的观测值,也就是具体数据.2.个案(case):每一个具体的调查对象或事件就是个案,每一个案大多在不同的属性上表现出了不同的具体的观测值(三)随机变量随机变量:在统计学上,取值之前不能准确地预料到什么值的变量\n\n三、总体、样本与个体1.总体(population):又称全域,指具有某种特征的一类事物的全体。总体是所欲研究的某一类对象的全体,总体的大小随研究的问题而改变2.个体(individual):构成总体的每个基本单元3.样本(sample):从总体中抽取的一部分个体4.样本大小(samplesize)或样本容量(capacityofsample):实验中被试的数目,或一个观测重复的次数,通常用n表示;样本容量超过30的为大样本,少于30的为小样本。5.有限个体的数目通常用N表示6.总体、个体与样本之间的关系\n总体样本样本是从总体中抽取的作为观察对象的一部分个体。\n总体(N)样本容量样本包含的个体数目大样本n>30小样本n<30样本(n)相对性总体(N)\n四、次数、比率、频率与概率1.事件:在一项研究中,对随机现象进行观察试验,在一定条件下,本质不同的事物可能出现,也可能不出现,这种事情称为随机事件,简称事件。2.频数(frequency):是指某一事件在某一类别中出现的数目或次数,用f表示3.比率:两个数的比4.频率:又称相对次数,即某一事件发生的次数被总的事件数目除,通常用比例(proportion)或百分数(percent)表示5.概率(probality):又称机率、或然率,用符号P表示,指某一事件在无限的观测中所能预料的相对出现的次数,也就是某一事物或某种情况在某一总体中出现的频率。\n五、参数和统计量1.参数(parameter):是指总体的特性,是描述总体情况的统计指标,用希腊字母表示,如:μ、σ、ρ2.统计量(statistics):是指样本的特征值,用英文字母表示,如:X、S、R\n平均数标准差相关系数统计量参数参数与统计量参数:统计量:参数与统计量的符号系统量数总体特性样本特性