统计学教材课后习题答案 21页

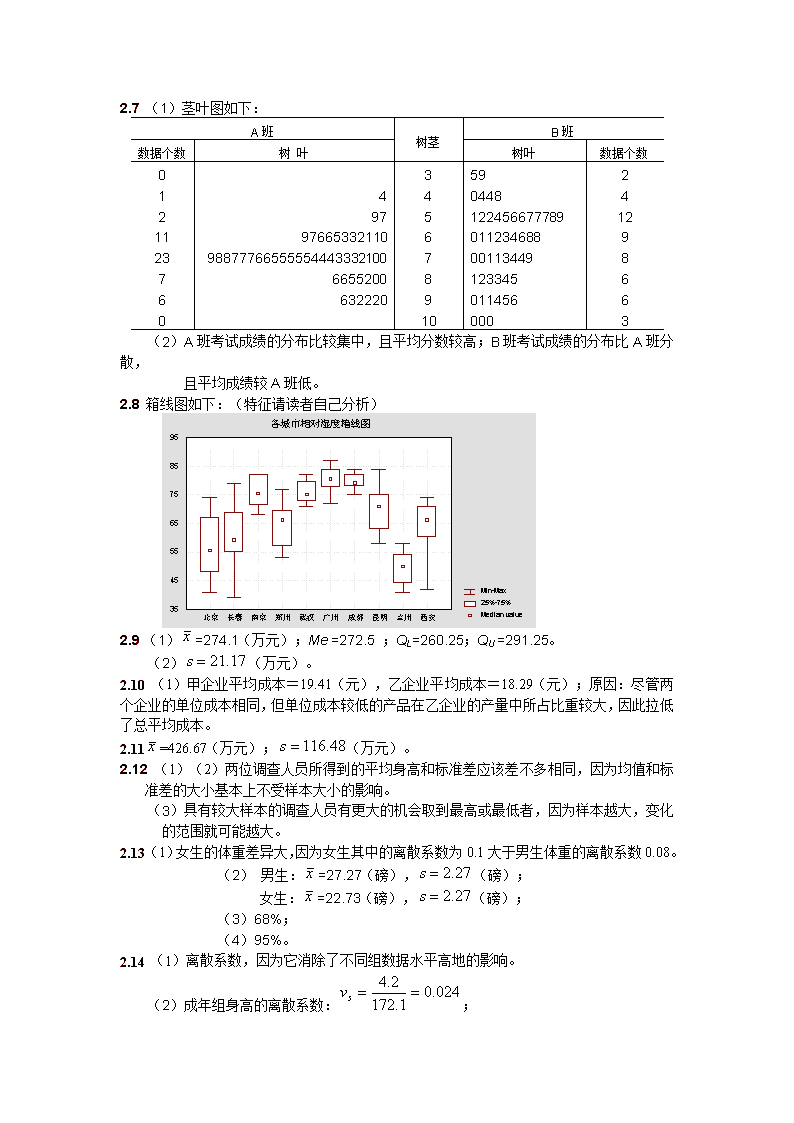
第2章统计数据的描述答案2.1（1）属于顺序数据。（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频率）频率%A1414B2121C3232D1818E1515合计100100（3）条形图（略）2.2（1）频数分布表如下：40个企业按产品销售收入分组表按销售收入分组（万元）企业数（个）频率（%）向上累积向下累积企业数频率企业数频率100以下100～110110～120120～130130～140140以上591274312.522.530.017.510.07.55142633374012.535.065.082.592.5100.04035261473100.087.565.035.017.57.5合计40100.0————（2）某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40100.02.3频数分布表如下：某百货公司日商品销售额分组表按销售额分组（万元）频数（天）频率（%）25～3030～3535～4040～4545～5046159610.015.037.522.515.0合计40100.0直方图（略）。\n2.4（1）排序略。（2）频数分布表如下：100只灯泡使用寿命非频数分布按使用寿命分组（小时）灯泡个数（只）频率（%）650~66022660~67055670~68066680~6901414690~7002626700~7101818710~7201313720~7301010730~74033740~75033合计100100直方图（略）。（3）茎叶图如下：6518661456867134679681123334555889969001111222334455666778888997000112234566677888971002233567788972012256789973356741472.5（1）属于数值型数据。（2）分组结果如下：分组天数（天）-25~-206-20~-158-15~-1010-10~-513-5~0120~545~107合计60（3）直方图（略）。2.6（1）直方图（略）。（2）自学考试人员年龄的分布为右偏。\n2.7（1）茎叶图如下：A班树茎B班数据个数树叶树叶数据个数03592144044842975122456677789121197665332110601123468892398877766555554443332100700113449876655200812334566632220901145660100003（2）A班考试成绩的分布比较集中，且平均分数较高；B班考试成绩的分布比A班分散，且平均成绩较A班低。2.8箱线图如下：（特征请读者自己分析）2.9（1）=274.1（万元）；Me=272.5；QL=260.25；QU=291.25。（2）（万元）。2.10（1）甲企业平均成本＝19.41（元），乙企业平均成本＝18.29（元）；原因：尽管两个企业的单位成本相同，但单位成本较低的产品在乙企业的产量中所占比重较大，因此拉低了总平均成本。2.11=426.67（万元）；（万元）。2.12（1）（2）两位调查人员所得到的平均身高和标准差应该差不多相同，因为均值和标准差的大小基本上不受样本大小的影响。（3）具有较大样本的调查人员有更大的机会取到最高或最低者，因为样本越大，变化的范围就可能越大。2.13（1）女生的体重差异大，因为女生其中的离散系数为0.1大于男生体重的离散系数0.08。（2）男生：=27.27（磅），（磅）；女生：=22.73（磅），（磅）；（3）68%；（4）95%。2.14（1）离散系数，因为它消除了不同组数据水平高地的影响。（2）成年组身高的离散系数：；\n幼儿组身高的离散系数：；由于幼儿组身高的离散系数大于成年组身高的离散系数，说明幼儿组身高的离散程度相对较大。2.15表给出了一些主要描述统计量，请读者自己分析。方法A方法B方法C平均165.6平均128.73平均125.53中位数165中位数129中位数126众数164众数128众数126标准偏差2.13标准偏差1.75标准偏差2.77极差8极差7极差12最小值162最小值125最小值116最大值170最大值132最大值1282.16（1）方差或标准差；（2）商业类股票；（3）（略）。2.17（略）。第3章概率与概率分布答案3.1设A＝女性，B＝工程师，AB＝女工程师，A+B＝女性或工程师（1）P(A)＝4/12＝1/3（2）P(B)＝4/12＝1/3（3）P(AB)＝2/12＝1/6（4）P(A+B)＝P(A)＋P(B)－P(AB)＝1/3＋1/3－1/6＝1/23.2求这种零件的次品率，等于计算“任取一个零件为次品”（记为A）的概率。考虑逆事件“任取一个零件为正品”，表示通过三道工序都合格。据题意，有：于是3.3设A表示“合格”，B表示“优秀”。由于B＝AB，于是＝0.8×0.15＝0.123.4设A＝第1发命中。B＝命中碟靶。求命中概率是一个全概率的计算问题。再利用对立事件的概率即可求得脱靶的概率。＝0.8×1＋0.2×0.5＝0.9脱靶的概率＝1－0.9＝0.1或（解法二）：P(脱靶)＝P(第1次脱靶)×P(第2次脱靶)＝0.2×0.5＝0.1\n3.5设A＝活到55岁，B＝活到70岁。所求概率为：3.6这是一个计算后验概率的问题。设A＝优质率达95％，＝优质率为80％，B＝试验所生产的5件全部优质。P(A)＝0.4，P()＝0.6，P(B|A)=0.955，P(B|)=0.85，所求概率为：决策者会倾向于采用新的生产管理流程。3.7令A1、A2、A3分别代表从甲、乙、丙企业采购产品，B表示次品。由题意得：P(A1)＝0.25，P(A2)＝0.30，P(A3)＝0.45；P(B|A1)＝0.04，P(B|A2)＝0.05，P(B|A3)＝0.03；因此，所求概率分别为：（1）＝0.25×0.04＋0.30×0.05＋0.45×0.03＝0.0385（2）3.8据题意，在每个路口遇到红灯的概率是p＝24/(24+36)＝0.4。设途中遇到红灯的次数＝X，因此，X～B(3，0.4)。其概率分布如下表：xi0123P(X=xi)0.2160.4320.2880.064期望值（均值）＝1.2（次），方差＝0.72，标准差＝0.8485（次）3.9设被保险人死亡数＝X，X～B(20000，0.0005)。（1）收入＝20000×50（元）＝100万元。要获利至少50万元，则赔付保险金额应该不超过50万元，等价于被保险人死亡数不超过10人。所求概率为：P(X≤10)＝0.58304。（2）当被保险人死亡数超过20人时，保险公司就要亏本。所求概率为：P(X>20)＝1－P(X≤20)＝1－0.99842＝0.00158（3）支付保险金额的均值＝50000×E(X)＝50000×20000×0.0005（元）＝50（万元）支付保险金额的标准差＝50000×σ(X)＝50000×(20000×0.0005×0.9995)1/2＝158074（元）3.10（1）可以。当n很大而p很小时，二项分布可以利用泊松分布来近似计算。本例中，λ=np=20000×0.0005=10，即有X～P(10)。计算结果与二项分布所得结果几乎完全一致。（2）也可以。尽管p很小，但由于n非常大，np和np(1-p)都大于5，二项分布也可以利用正态分布来近似计算。本例中，np=20000×0.0005=10，np(1-p)=20000×0.0005×(1-0.0005)=9.995，即有X～N(10,9.995)。相应的概率为：P(X≤10.5)＝0.51995，P(X≤20.5)＝0.853262。可见误差比较大（这是由于P太小，二项分布偏斜太严重）。\n【注】由于二项分布是离散型分布，而正态分布是连续性分布，所以，用正态分布来近似计算二项分布的概率时，通常在二项分布的变量值基础上加减0.5作为正态分布对应的区间点，这就是所谓的“连续性校正”。（3）由于p＝0.0005，假如n=5000，则np＝2.5<5，二项分布呈明显的偏态，用正态分布来计算就会出现非常大的误差。此时宜用泊松分布去近似。3.11（1）＝0.04779合格率为1-0.04779＝0.95221或95.221％。(2)设所求值为K，满足电池寿命在200±K小时范围内的概率不小于0.9，即有：即：，K/30≥1.64485,故K≥49.3456。3.12设X＝同一时刻需用咨询服务的商品种数，由题意有X～B(6,0.2)（1）X的最可能值为：X0＝[(n+1)p]＝[7×0.2]＝1（取整数）（2）＝1-0.9011＝0.0989第4章抽样与抽样分布答案4.1⑴20,2；⑵近似正态；⑶-2.25；⑷1.50。4.2⑴0.0228；⑵0.0668；⑶0.0062；⑷0.8185；⑸0.0013。4.3⑴0.8944；⑵0.0228；⑶0.1292；⑷0.9699。4.4⑴101,99⑵1；⑶不必。4.5趋向正态。4.6⑴正态分布,213,4.5918；⑵0.5,0.031,0.938。4.7⑴406,1.68,正态分布；⑵0.001；⑶是，因为小概率出现了。4.8⑴增加；⑵减少。4.9⑴正态；⑵约等于0；⑶不正常；⑷正态,0.06。4.10⑴0.015；⑵0.0026；⑶0.1587。4.11⑴(0.012,0.028)；⑵0.6553,0.7278。4.12⑴0.05；⑵1；⑶0.000625。\n第5章参数估计答案5.1（1）；（2）E=1.55。5.2（1）；（2）E=4.2；（3）（115.8,124.2）。5.3（2.88,3.76）；(2.80,3.84)；(2.63,4.01)。5.4（7.1,12.9）。5.5（7.18,11.57）。5.6（18.11%,27.89%）；（17.17%,22.835）。5.7(1)（51.37%,76.63%）；（2）36。5.8（1.86,17.74）；（0.19,19.41）。5.9（1）2±1.176；（2）2±3.986；（3）2±3.986；（4）2±3.587；（5）2±3.364。5.10（1），；（2）1.75±4.27。5.11（1）10%±6.98%；（2）10%±8.32%。5.12（4.06,14.35）。5.1348。5.14139。5.1557。5.16769。第6章假设检验答案6.1研究者想要寻找证据予以支持的假设是“新型弦线的平均抗拉强度相对于以前提高了”，所以原假设与备择假设应为：6.2＝“某一品种的小鸡因为同类相残而导致的死亡率”，6.3，。6.4（1）第一类错误是该供应商提供的这批炸土豆片的平均重量的确大于等于60克，但检验结果却提供证据支持店方倾向于认为其重量少于60克；（2）第二类错误是该供应商提供的这批炸土豆片的平均重量其实少于60克，但检验结果却没有提供足够的证据支持店方发现这一点，从而拒收这批产品；（3）连锁店的顾客们自然看重第二类错误，而供应商更看重第一类错误。6.5（1）检验统计量，在大样本情形下近似服从标准正态分布；（2）如果，就拒绝；（3）检验统计量＝2.94>1.645，所以应该拒绝。\n6.1＝3.11，拒绝。6.2＝1.93，不拒绝。6.3＝7.48，拒绝。6.4＝206.22，拒绝。6.5＝-5.145，拒绝。6.6＝1.36，不拒绝。6.7＝-4.05，拒绝。6.8＝8.28，拒绝。6.9（1）检验结果如下：t-检验:双样本等方差假设变量1变量2平均100.7109.9方差24.1157894733.35789474观测值2020合并方差28.73684211假设平均差0df38tStat-5.427106029P(T≤t)单尾1.73712E-06t单尾临界1.685953066P(T≤t)双尾3.47424E-06t双尾临界2.024394234t-检验:双样本异方差假设变量1变量2平均100.7109.9方差24.1157894733.35789474观测值2020假设平均差0df37tStat-5.427106029P(T≤t)单尾1.87355E-06t单尾临界1.687094482P(T≤t)双尾3.74709E-06t双尾临界2.026190487（2）方差检验结果如下：\nF-检验双样本方差分析变量1变量2平均100.7109.9方差24.1157894733.35789474观测值2020df1919F0.722940991P(F≤f)单尾0.243109655F单尾临界0.395811384第7章方差分析与试验设计答案7.1(或)，不能拒绝原假设。7.2(或)，拒绝原假设。，拒绝原假设；，不能拒绝原假设；，拒绝原假设。7.3方差分析表中所缺的数值如下表：差异源SSdfMSFP值F临界值组间42022101.4780.2459463.354131组内383627142.07———总计425629————(或)，不能拒绝原假设。7.4有5种不同品种的种子和4种不同的施肥方案，在20快同样面积的土地上，分别采用5种种子和4种施肥方案搭配进行试验，取得的收获量数据如下表：(或)，拒绝原假设。(或)，拒绝原假设。7.5(或)，不能拒绝原假设。(或)，不能拒绝原假设。7.6(或)，拒绝原假设。(或)，不能拒绝原假设。\n(或)，不能拒绝原假设。第8章相关与回归分析答案8.1（1）利用Excel计算结果可知,相关系数为，说明相关程度较高。（2）计算t统计量给定显著性水平=0.05，查t分布表得自由度n-2=10-2=8的临界值为2.306，显然，表明相关系数r在统计上是显著的。8.2利用Excel中的”数据分析”计算各省市人均GDP和第一产业中就业比例的相关系数为:-0.34239，这说明人均GDP与第一产业中就业比例是负相关，但相关系数只有-0.34239，表明二者负相关程度并不大。相关系数检验：在总体相关系数的原假设下，计算t统计量：查t分布表，自由度为31-2=29，当显著性水平取时，=2.045；当显著性水平取时，=1.699。由于计算的t统计量的绝对值1.9624小于=2.045，所以在的显著性水平下，不能拒绝相关系数的原假设。即是说，在的显著性水平下不能认为人均GDP与第一产业中就业比例有显著的线性相关性。但是计算的t统计量的绝对值1.9624大于=1.699，所以在的显著性水平下,可以拒绝相关系数的原假设。即在的显著性水平下，可以认为人均GDP与第一产业中就业比例有一定的线性相关性。8.3设当年红利为Y，每股账面价值为X建立回归方程估计参数为参数的经济意义是每股账面价值增加1元时，当年红利将平均增加0.072876元。序号6的公司每股账面价值为19.25元，增加1元后为20.25元，当年红利可能为：(元)8.4（1）数据散点图如下：\n（2）根据散点图可以看出，随着航班正点率的提高，投诉率呈现出下降的趋势，两者之间存在着一定的负相关关系。（3）设投诉率为Y，航班正点率为X建立回归方程估计参数为（4）参数的经济意义是航班正点率每提高一个百分点，相应的投诉率（次/10万名乘客）下降0.07。（5）航班按时到达的正点率为80%，估计每10万名乘客投诉的次数可能为：（次/10万）8.5由Excel回归输出的结果可以看出：（1）回归结果为（2）由Excel的计算结果已知：对应的t统计量分别为0.51206、4.853871、4.222811、3.663731,其绝对值均大于临界值,所以各个自变量都对Y有明显影响。由F=58.20479,大于临界值，说明模型在整体上是显著的。8.6（1）该回归分析中样本容量是14+1=15；（2）计算RSS=66042-65965=77；ESS的自由度为k-1=2，RSS的自由度n－k=15-3=12；（3）计算：可决系数修正的可决系数（4）检验X2和X3对Y是否有显著影响(5)F统计量远比F临界值大，说明X2和X3联合起来对Y有显著影响，但并不能确定X2\n和X3各自对Y的贡献为多少。8.7来源平方和自由度方差来自回归2179.5612179.56来自残差99.11224.505总离差平方和2278.67238.8（1）用Excel输入Y和X数据，生成和的数据，用Y对X、、回归，估计参数结果为t=(-1.9213)(2.462897)(-2.55934)(3.118062)（2）检验参数的显著性：当取时，查t分布表得，与t统计量对比，除了截距项外，各回归系数对应的t统计量的绝对值均大于临界值，表明在这样的显著性水平下，回归系数显著不为0。（3）检验整个回归方程的显著性：模型的,，说明可决系数较高，对样本数据拟合较好。由于F=98.60668，而当取时，查F分布表得，因为F=98.60668>4.07，应拒绝，说明X、、联合起来对Y确有显著影响。（4）计算总成本对产量的非线性相关系数：因为因此总成本对产量的非线性相关系数为或R=0.9867466（5）评价：虽然经t检验各个系数均是显著的，但与临界值都十分接近，说明t检验只是勉强通过，其把握并不大。如果取，则查t分布表得，这时各个参数对应的t统计量的绝对值均小于临界值，则在的显著性水平下都应接受的原假设。8.9利用Excel输入X、y数据，用y对X回归，估计参数结果为t值=（9.46）（-6.515）整理后得到：第9章时间序列分析答案\n9.1（1）30××=30×1.3131=39.393（万辆）（2）（3）设按7.4%的增长速度n年可翻一番则有所以n=log2/log1.074=9.71（年）故能提前0.29年达到翻一番的预定目标。9.2（1）以1987年为基期，2003年与1987年相比该地区社会商品零售额共增长：（2）年平均增长速度为=0.0833=8.33%（3）2004年的社会商品零售额应为（亿元）9.3（1）发展总速度平均增长速度=（2）（亿元）（3）平均数（亿元），2002年一季度的计划任务：（亿元）。9.4(1)用每股收益与年份序号回归得。预测下一年(第11年)的每股收益为元(2)时间数列数据表明该公司股票收益逐年增加，趋势方程也表明平均每年增长0.193元。是一个较为适合的投资方向。9.5（1）移动平均法消除季节变动计算表年别季别鲜蛋销售量四项移动平均值移正平均值（）2000年一季度13.1—二季度13.910.875—三季度7.910.310.5875四季度8.69.7102001年一季度10.810.159.925二季度11.510.7510.45三季度9.711.711.225四季度1113.212.452002年一季度14.614.77513.9875二季度17.516.57515.675三季度1617.52517.05四季度18.218.1517.83752003年一季度18.418.37518.2625\n二季度2018.32518.35三季度16.9四季度18（2）（3）趋势剔出法季节比例计算表（一）年别季别时间序列号t鲜蛋销售量预测鲜蛋销售量趋势剔除值2000年一季度113.19.3323529411.403718878二季度213.99.9722058821.39387415三季度37.910.612058820.74443613四季度48.611.251911760.7643145612001年一季度510.811.891764710.908191531二季度611.512.531617650.917678812三季度79.713.171470590.736440167四季度81113.811323530.7964479272002年一季度914.614.451176471.010298368二季度1017.515.091029411.159629308三季度111615.730882351.0171076四季度1218.216.370735291.1117399232003年一季度1318.417.010588241.081679231二季度142017.650441181.133116153三季度1516.918.290294120.923987329四季度161818.930147060.950864245上表中，其趋势拟合为直线方程。趋势剔出法季节比例计算表（二）季度年度一季度二季度三季度四季度2000年1.4037191.3938740.7444360.764315—2001年0.9081920.9176790.736440.796448—2002年1.0102981.1596291.0171081.11174—2003年1.0816791.1331160.9239870.950864—平均1.1009721.1510750.8554930.9058424.013381季节比率%1.0973011.1472370.8526410.9028224．00000根据上表计算的季节比率，按照公式计算可得：2004年第一季度预测值：2004年第二季度预测值：2004年第三季度预测值：2004年第四季度预测值：\n9.1(1)用原始资料法计算的各月季节比率为:月份1月2月3月4月5月6月季节比率0.91950.78680.99311.00291.02881.0637月份7月8月9月10月11月12月季节比率0.97220.98511.04071.03501.07651.0958平均法计算季节比率表：年别月份2000年2001年2002年2003年平均季节比率%1月4.785.186.466.825.808750.91952月3.974.615.625.684.970250.78683月5.075.696.967.386.27350.99314月5.125.717.127.406.335751.00295月5.275.907.237.606.499251.02886月5.456.057.437.956.71951.06377月4.955.656.787.196.14150.97228月5.035.766.767.356.2230.98519月5.376.147.037.766.5741.040710月5.346.146.857.836.538251.035011月5.546.477.038.176.800251.076512月5.446.557.228.476.92251.0958平均6.3172081.0000季节比率的图形如下：(2)用移动平均法分析其长期趋势年月序号工业总产值(亿元)移动平均移正平均Jan-0014.78Feb-0023.97Mar-0035.07Apr-0045.12May-0055.27\nJun-0065.455.13Jul-0074.955.17Aug-0085.035.22Sep-0095.375.27Oct-00105.345.32Nov-00115.545.37Dec-00125.445.115.43Jan-01135.185.145.49Feb-01144.615.205.55Mar-01155.695.255.62Apr-01165.715.305.69May-01175.905.355.77Jun-01186.055.405.87Jul-01195.655.465.97Aug-01205.765.526.06Sep-01216.145.586.18Oct-01226.145.656.29Nov-01236.475.736.40Dec-01246.555.826.51Jan-02256.465.936.60Feb-02265.626.016.68Mar-02276.966.126.74Apr-02287.126.236.80May-02297.236.356.85Jun-02307.436.466.89Jul-02316.786.556.91Aug-02326.766.646.93Sep-02337.036.716.96Oct-02346.856.776.98Nov-02357.036.827.02Dec-02367.226.887.06Jan-03376.826.917.10Feb-03385.686.917.15Mar-03397.386.947.23Apr-03407.406.977.31May-03417.607.007.41Jun-03427.957.04Jul-03437.197.08Aug-03447.357.12Sep-03457.767.19Oct-03467.837.27Nov-03478.177.36Dec-03488.477.46\n原时间序列与移动平均的趋势如下图所示：9.1（1）采用线性趋势方程法：剔除其长期趋势。趋势分析法剔除长期趋势表年月序号工业总产值(亿元)长期趋势值剔除长期趋势Jan-831477.9467.06721.023193Feb-832397.2474.07370.837844Mar-833507.3481.08021.054502Apr-834512.2488.08671.049404May-835527495.09321.064446Jun-836545502.09971.085442Jul-837494.7509.10620.971703Aug-838502.5516.11270.973625Sep-839536.5523.11921.025579Oct-8310533.5530.12571.006365Nov-8311553.6537.13221.030659Dec-8312543.9544.13870.999561Jan-8413518551.14520.939861Feb-8414460.9558.15170.825761Mar-8415568.7565.15821.006267Apr-8416570.5572.16470.997091May-8417590579.17121.018697Jun-8418604.8586.17771.031769Jul-8419564.9593.18420.952318Aug-8420575.9600.19070.959528Sep-8421613.9607.19721.011039Oct-8422614614.20370.999668Nov-8423646.7621.21021.041032Dec-8424655.3628.21671.043111Jan-8525645.7635.22321.016493Feb-8526562.4642.22970.875699Mar-8527695.7649.23621.071567\nApr-8528712656.24271.084964May-8529723.1663.24921.090239Jun-8530743.2670.25571.108831Jul-8531678677.26221.001089Aug-8532676684.26870.987916Sep-8533703691.27521.016961Oct-8534685.3698.28170.981409Nov-8535703.3705.28820.997181Dec-8536722.4712.29471.014187Jan-8637681.9719.30120.948003Feb-8638567.6726.30770.781487Mar-8639737.7733.31421.005981Apr-8640739.6740.32070.999027May-8641759.6747.32721.016422Jun-8642794.8754.33371.053645Jul-8643719761.34020.944387Aug-8644734.8768.34670.956339Sep-8645776.2775.35321.001092Oct-8646782.5782.35971.000179Nov-8647816.5789.36621.034374Dec-8648847.4796.37271.064075剔除长期趋势后分析其季节变动情况表年份月份1983年1984年1985年1986年季节比率%1月1.0231930.9398611.0164930.9480030.9818882月0.8378440.8257610.8756990.7814870.8301983月1.0545021.0062671.0715671.0059811.0345794月1.0494040.9970911.0849640.9990271.0326225月1.0644461.0186971.0902391.0164221.0474516月1.0854421.0317691.1088311.0536451.0699227月0.9717030.9523181.0010890.9443870.9673748月0.9736250.9595280.9879160.9563390.9693529月1.0255791.0110391.0169611.0010921.01366810月1.0063650.9996680.9814091.0001790.99690511月1.0306591.0410320.9971811.0343741.02581212月0.9995611.0431111.0141871.0640751.030234（3）运用分解法可得到循环因素如下图：\n第10章统计指数答案10.1（1）；（2）。（3）略。10.2；；。10.3（1）。（2）略。10.4（1）；（2）；（3）；（4）略。10.5；；。10.6⑴；⑵；⑶；⑷。10.7⑴⑵，⑶，\n10.8依据有关公式列表计算各企业的工业经济效益综合指数如下：各企业经济效益综合指数一览表(标准比值法)参评指标标准比值或个体指数(%)权数A企业B企业C企业D企业E企业产品销售率77.3592.3397.9792.7487.6115资金利税率90.04104.0699.6384.87103.3230成本利润率90.37112.9699.88101.0782.0515增加值率87.24100.0098.2887.5992.0710劳动生产率93.47101.85116.84109.5987.0310资金周转率87.43101.09114.75103.8398.3620综合指数87.73102.41104.0395.0194.03──排名52134──10.9依据有关公式列表计算各企业的工业经济效益综合指数如下表：各企业经济效益综合指数一览表(改进的功效系数法)参评指标阈值改进的功效系数权数满意值不允许值A企业B企业C企业D企业E企业产品销售率95.5074.5060.0089.52100.0090.2980.7615资金利税率14.1011.5070.77100.0090.7760.0098.4630成本利润率9.506.9070.77100.0083.0884.6260.0015增加值率29.0025.3060.00100.0094.5961.0875.1410劳动生产率7250540068.6579.89100.0090.2760.0010资金周转率2.101.6060.0080.00100.0084.0076.0020综合指数────65.5091.9793.9574.9778.05──排名────52143──上面两种方法给出的综合评价结果的差异表现在D、E两个企业的综合经济效益排名不同。原因在于两种方法的对比标准不同(以下具体说明)。第12章国民经济统计基础知识答案12.1生产法GDP=168760亿元；分配法GDP=168755亿元使用法GDP=154070亿元国内生产净值=149755亿元（按生产法计算）国民总收入=165575亿元（按收入法计算）国民可支配总收入=167495亿元国民可支配净收入=148490亿元消费率=67.95%（按可支配总收入计算）储蓄率=32.05%（按可支配总收入计算）投资率=27.31%（按使用法GDP计算）\n12.2国民财富总额为：216765亿元12.3生产法GDP增长速度为8.69%，紧缩价格指数为102.83%；使用法GDP增长速度为8.25%，紧缩价格指数为103.25%。