统计学b卷-含答案 6页

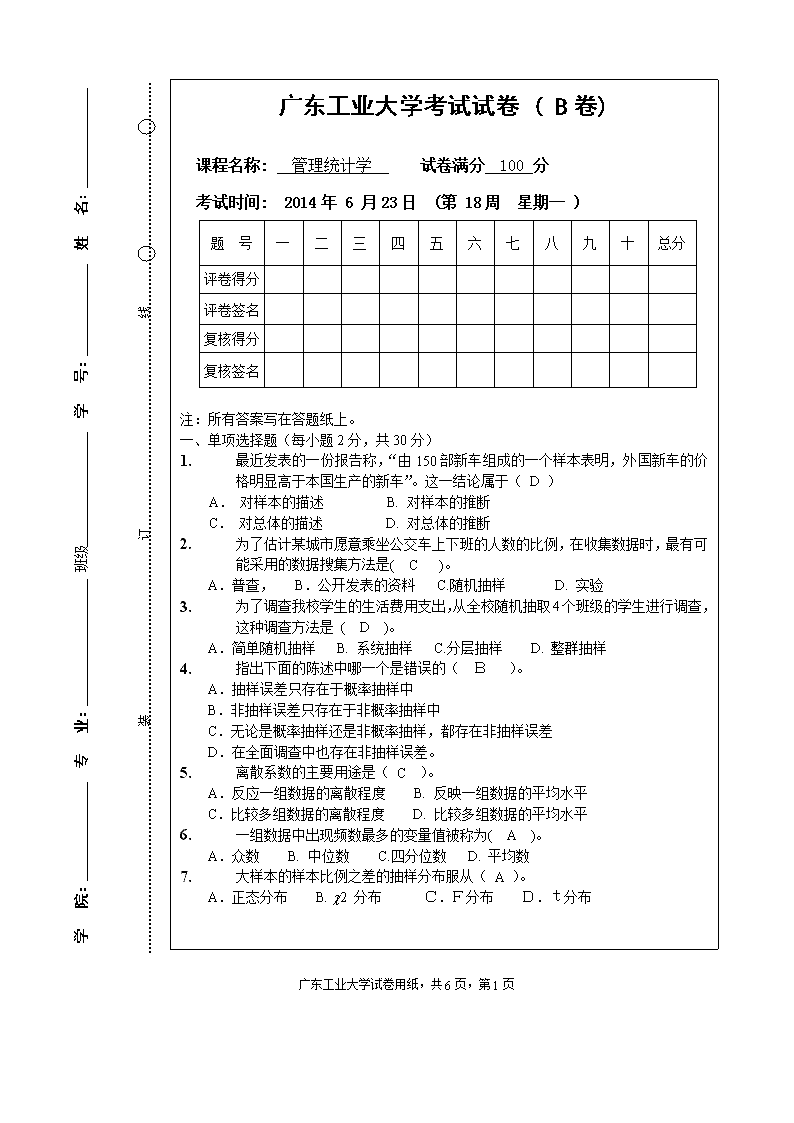
广东工业大学考试试卷(B卷)课程名称:管理统计学试卷满分100分考试时间:2014年6月23日(第18周星期一)题号一二三四五六七八九十总分评卷得分评卷签名复核得分复核签名注：所有答案写在答题纸上。一、单项选择题（每小题2分，共30分）1.最近发表的一份报告称，“由150部新车组成的一个样本表明，外国新车的价格明显高于本国生产的新车”。这一结论属于（D）A．对样本的描述B.对样本的推断C．对总体的描述D.对总体的推断2.为了估计某城市愿意乘坐公交车上下班的人数的比例，在收集数据时，最有可能采用的数据搜集方法是(C)。A．普查，B．公开发表的资料C.随机抽样D.实验3.为了调查我校学生的生活费用支出，从全校随机抽取4个班级的学生进行调查，这种调查方法是(D)。A．简单随机抽样B.系统抽样C.分层抽样D.整群抽样4.指出下面的陈述中哪一个是错误的（Ｂ）。A．抽样误差只存在于概率抽样中B．非抽样误差只存在于非概率抽样中C．无论是概率抽样还是非概率抽样，都存在非抽样误差D．在全面调查中也存在非抽样误差。5.离散系数的主要用途是（C）。A．反应一组数据的离散程度B.反映一组数据的平均水平C．比较多组数据的离散程度D.比较多组数据的平均水平6.一组数据中出现频数最多的变量值被称为(A)。A．众数B.中位数C.四分位数D.平均数7.大样本的样本比例之差的抽样分布服从（A）。A．正态分布B.c2分布　　　Ｃ．Ｆ分布　　Ｄ．ｔ分布学院：专业：班级学号：姓名：装订线广东工业大学试卷用纸，共6页，第6页\n8.从一个均值，标准差的总体中随机选取容量为n=36的样本。假定该总体并不是很偏，则样本均值小于19.8的近似概率为（A）。（注：已知标准正态分布的分布函数Φ(1)=0.8413）A．0.1587B.0.8413C.0.3174D.0.63249.一个95%的置信区间是指（C）。A．总体参数有95%的概率落在这一区间内B.总体参数有95%的概率未落在这一区间内Ｃ．在用同样的方法构造的总体参数的多个区间中，有95%的区间包含该总体参数Ｄ．在用同样的方法构造的总体参数的多个区间中，有95%的区间不包含该总体参数10.正态总体，方差未知时，在小样本条件下，总体均值在1-α置信水平下的置信区间为（B）。A.B.C.D.11.在假设检验中，第一类错误是指（A）。A.当原假设正确时拒绝原假设B.当原假设错误时拒绝原假设C.当原假设错误时接受原假设D.当备择假设不正确时未拒绝被择假设12.双因素方差分析涉及（Ａ）Ａ．两个分类型自变量　　　Ｂ．两个数值型自变量　　Ｃ．两个分类型因变量　　　Ｄ．两个数值型因变量13.在双因素反差分析中，度量两个分类自变量对因变量的影响的统计量是R2，其计算公式为（A）。A.B.C.D.14.在回归估计中，自变量的取值x0越远离其平均值，求得的y的预测区间（A）。A.越宽B.越窄C.越准确D.越接近实际值15.标准化残差图主要用于直观地判断（C）。A.回归模型的线性关系是否显著B.回归系数是否显著C.误差项ε服从正态分布的假设是否成立D.误差项ε等方差的假设是否成立二、填空题（每空2分，共20分）1.如果在样本加工为统计量的过程中，样本中所含的信息可能有所损失，若在将样广东工业大学试卷用纸，共6页，第6页\n本加工为统计量时，信息毫无损失，则称此统计量为充分统计量而中位数、分位数、四分位数则都是次序统计量。1.正态总体，方差未知时，在小样本条件下，总体均值在1-α置信水平下的置信区间为。2.参数估计是指用样本统计量去估计总体的参数；具体包括点估计与区间估计两类。3.Oneway-ANOVA时，从3个总体中各选取了4个观察值，得到SST=1364，SSE=828，组间均方为268，组内均方为92。4.假设检验中的第一类错误又被称为弃真错误，其发生的概率是α。三、计算分析题（共计50分）1.已知某一样本的样本均值，样本标准差，样本容量，请构造置信水平95%的置信区间。（注：，）解：因为总体分布未知，但是样本容量75为大样本，所以根据中心极限定理，样本均值服从正态分布。且所以总体均值μ的置信区间半径为所以置信区间为（114.2，125）。2.根据以往的生产数据，某种产品的废品率为5%。如果要求95%的置信区间，估计误差不超过2%，样本容量n应为多大？解：由题意知，π=0.05，E=0.02，α=0.05对总体比例π的估计的误差是，所以广东工业大学试卷用纸，共6页，第6页\n1.（18分）在一项关于儿童身体情况的调查中，在全国各城市随机地抽取了若干名周岁的儿童进行调查。其中在北京抽得的5名儿童的身高分别是（厘米）：84.00，75.00，78.00，76.00，67.00；而在上海抽得的5名儿童的身高分别是（厘米）：72.00，71.00，74.00，74.00，73.00。用EXCEL分析得到如下结果：t-检验:双样本等方差假设　北京上海平均74.673.6方差32.82.3观测值55合并方差17.55假设平均差0df8tStat0.377426P(T<=t)单尾0.357837t单尾临界1.859548P(T<=t)双尾0.715673t双尾临界2.306004　t-检验:双样本异方差假设　北京上海平均74.673.6方差32.82.3观测值55假设平均差0df5tStat0.377426P(T<=t)单尾0.360674t单尾临界2.015048P(T<=t)双尾0.721347t双尾临界2.570582　1）首先请以显著性水平为α=5%检验二者方差是否相等？(已知)2）试分析在显著性水平为α=5%时，两市周岁儿童的身高是否存在显著差异。解：1）已知北京儿童的身高样本方差为，上海儿童的身高的样本方差为；所以所以以显著性水平为α=5%拒绝原假设H0，即认为二者方差之间存在着显著差异。2）因为二者方差存在显著差异，所以使用双样本异方差假设下的t检验。因为检验二者均值是否相等，因此是双侧t检验，所以P值为0.721347157，大于显著性水平广东工业大学试卷用纸，共6页，第6页\nα，所以不拒绝原假设H0，也即不能证明两市周岁儿童身高存在显著差异。1.2.（14分）某厂为了调查其生产的某型设备的故障率，随机抽查了卖出的100台设备，发现其中35台在一年之内需要派人上门维修。　　（1）在95％的置信水平下，求一年之内需要上门维修设备比例的置信区间。（7分）（2）如果要求估计误差不超过5%，在相同条件下，应抽取多少台设备进行调查？（7分）（注：，）解：（1）由题意知，，。这是二项分布，则的点估计为0.35，置信水平95%的置信区间半径为：所以，设备维修比例的置信区间为(25.7%,44.3%)。…….7分（2）二项分布的置信水平95%的估计的误差为因为p未知，将其设定为0.5，欲使估计误差不超过5%，则：解得：…….7分3.（17分）某农科所试验在水溶液中种植西红柿,采用了三种施肥方式和四种不同的水温。三种施肥方式是：一次施肥、二次施肥与四次施肥。水温分别为4摄氏度,10摄氏度,16摄氏度,20摄氏度。试验结果的产量如下表: 施肥方式一次施肥二次施肥四次施肥水温冷(4摄氏度)374044凉(10摄氏度)303131温(16摄氏度)301911热(20摄氏度)191715  用方差分析方法，得到如下的表格：方差分析差异源SSdfMSFP-valueFcrit广东工业大学试卷用纸，共6页，第6页\n行1020.6670.0076174.757063列28.50.6531755.143253误差186.8333总计123611（1）请写出SSR、SSC、SSE的自由度；（2）计算MSR、MSC、MSE的值；（3）计算表中F统计量的值；（4）分析“施肥的方式”和“水温”对产量的影响是否显著。（α=0.05）解：1）df(SSR)=R-1=3df(SSC)=C-1=2df(SSE)=(R-1)(C-1)=6…….3分2)MSR=SSR/3=340.2MSC=SSC/2=14.25MSE=SSE/6=31.14…….6分3）FR=MSR/MSE=10.93FC=MSC/MSE=0.464)从表上可以看出行的P值0.007617，远小于显著性水平α，所以行因素即水温对产量存在着显著影响；列的P值0.653175远大于显著性水平α，所以列因素即施肥方式对产量不存在着显著影响。…….6分广东工业大学试卷用纸，共6页，第6页