工学高等钢筋混凝土结构混凝土的力学性能 63页

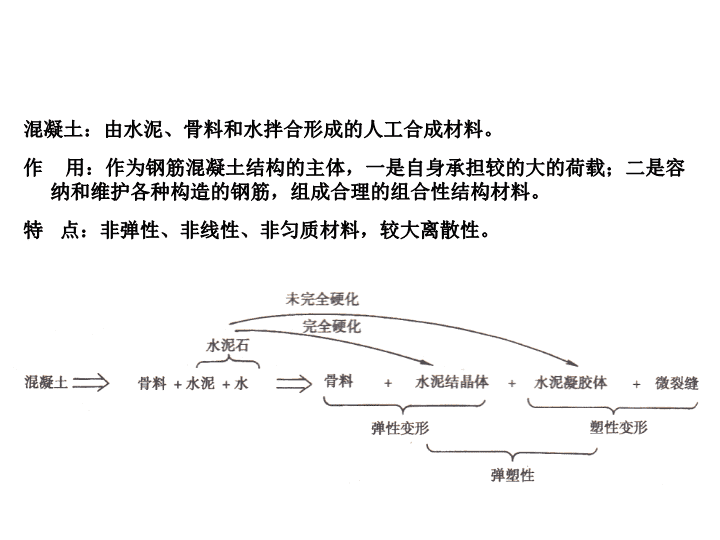
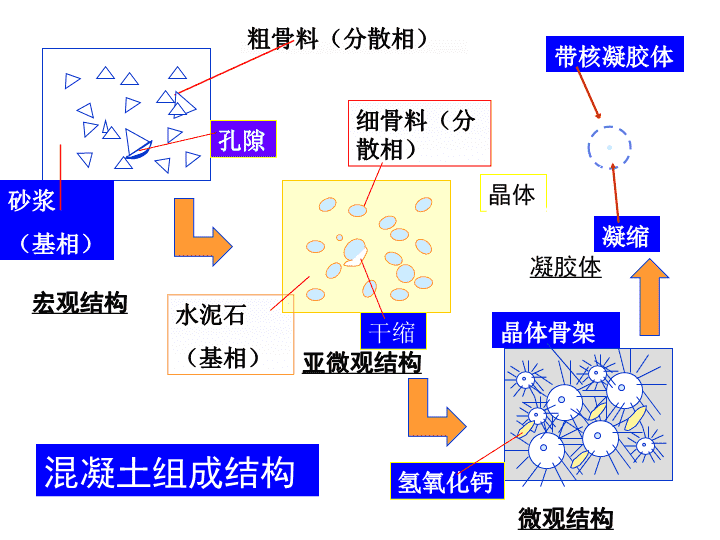
混凝土：由水泥、骨料和水拌合形成的人工合成材料。 作 用：作为钢筋混凝土结构的主体，一是自身承担较的大的荷载；二是容纳和维护各种构造的钢筋，组成合理的组合性结构材料。 特 点：非弹性、非线性、非匀质材料，较大离散性。 混凝土是由水泥、水、骨料按一定比例配合，经过硬化后形成的人工石。其为一多相复合材料，其质量的好坏与材料、施工配合比、施工工艺、龄期、环境等诸多因素有关。 第 1 章 基本力学性能 第一节 混凝土的变形及破坏机理 一 . 材料的组成和内部构造 通常把混凝土的结构分为三种类型： Ａ . 微观结构： 也即水泥石结构，包括水泥凝胶、晶体骨架、未水化完的水泥颗粒和凝胶孔组成。 Ｂ . 亚微观结构： 即混凝土中的水泥砂浆结构。 Ｃ . 宏观结构： 即砂浆和粗骨料两组分体系。 宏观结构 亚微观结构 微观结构 粗骨料（分散相） 水泥石 （基相） 细骨料（分散相） 砂浆 （基相） 晶体骨架 晶体 带核凝胶体 干缩 孔隙 凝缩 氢氧化钙 凝胶体 混凝土组成结构 晶体骨架： 由完全水化的水泥结晶体和骨料组成，承受外力，具有弹性变形特点。 塑性变形： 在外力作用下由凝胶、孔隙、微裂缝产生。 破坏起源： 孔隙、微裂缝等原因造成。 PH 值： 由于水泥石中的氢氧化钙存在，混凝土偏碱性。 由于水泥凝胶体的硬化过程需要若干年才能完成，所以，混凝土的强度、变形也会在较长时间内发生变化，强度逐渐增长，变形逐渐加大 。 由于混凝土材料的非均匀微构造、局部缺陷和离散性较大而极难获得精确的计算结果。因此，主要讨论混凝土结构的宏观力学反应，即混凝土结构在一定尺度范围内的平均值。 宏观结构中混凝土的两个基本构成部分，即粗骨料和水泥砂浆的随机分布，以及两者的物理和力学性能的差异是其非匀质、不等向性质的根本原因。 粗骨料和水泥浆体的物理力学性能指标的典型值 施工和环境因素引起混凝土的 非匀质性 和 不等向性 ：例如浇注和振捣过程中，比重和颗粒较大的骨料沉入构件的底部，而比重小的骨料和流动性大的水泥砂浆、气泡等上浮，靠近构件模板侧面和表面的混凝土表层内，水泥砂浆和气孔含 量 比内部的多；体积较大的结构，内部和表层的失水速率和含水 量 不等，内外温度差形成的微裂缝状况也有差别；建造大型结构时，常需留出水平的或其它形状的施工缝 …… 。 当混凝土承受不同方向（即平行、垂直或倾斜于混凝土的浇注方向）的应力时，其强度和变形值有所不同。 例如对混凝土立方体试件，标准试验方法规定沿垂直浇注方向加载以测定抗压强度， 其值略低于沿平行浇注方向加载的数值。再如，竖向浇注的混凝土柱，截面上混凝土性质对称，而沿柱高两端的性质有别；卧位浇注的混凝土柱，情况恰好相反。这两种柱在轴力作用下的强度和变形也将不等。 浇注方向 N N 浇注方向 N N ≤ 1.1.2 材性的基本特点 混凝土的材料组成和构造决定其 4 个基本受力特点 : 1 ．复杂的微观内应力、变形和裂缝状态 将一块混凝土按比例放大，可以看作是 由粗骨料和硬化水泥砂浆等两种主要材料构成的不规则的三维实体结构，且具有非匀质、非线性和不连续的性质 。 混凝土在承受荷载（应力）之前，就已经存在复杂的微观应力、应变和裂缝，受力后更有剧烈的变化。 在混凝土的凝固过程中，水泥的水化作用在表面形成凝胶体，水泥浆逐渐变稠、硬化，并和粗细骨料粘结成一整体。在此过程中，水泥浆失水收缩变形远大于粗骨料的。此收缩变形差使粗骨料受压，砂 浆 受拉。这些应力场在截面上的合力为零，但局部应力可能很大，以至在骨料界面产生微裂缝。 粗骨料和水泥砂桨的热工性能（如线膨胀系数 ) 有差别。当混凝土中水泥产生水化热或环境温度变化时，两者的温度变形差受到相互约束而形成温度应力场。 压力 拉力 当混凝土承受外力作用时，即使作用应力完全均匀，混凝土内也将产生 不均匀的空间微观应力场 。 在应力的长期作用下， 水泥砂浆和粗骨料的徐变差使混凝土内部发生应力重分布 ，粗骨料将承受更大的压应力。 所有这些都说明， 从微观上分析混凝土，必然要考虑非常复杂的、随机分布的三维应力（应变）状态 。 其对于混凝土的宏观力学性能，如开裂，裂缝开展，变形，极限强度和破坏形态等，都有重大影响。 混凝土内部有不可避免的初始气孔和缝隙，其尖端附近因收缩、温度变化或应力作用都会形成局部应力集中区，其应力分布更复杂，应力值更高。 2. 变形的多元组成 从砼的组成和构造特点分析，其变形值由 3 部分组成： ⑴骨料的弹性变形 占混凝土体积绝大部分的石子和砂，本身的强度和弹性模量值均比其组成的混凝土高出许多。即使混凝土达到极限强度值时，骨料并不破碎，变形仍在弹性范围以内，即 变形与应力成正比，卸载后变形可全部恢复，不留残余变形 。 ⑵ 水泥凝胶体的粘性流动 水泥经水化作用后生成的凝胶体，在应力作用下除了即时产生的变形外，还将随时间的延续而发生缓慢的粘性流（移）动，混凝土的变形不断地增长，形成塑性变形。 当卸载后，这部分变形一般不能恢复，出现残余变形。 ⑶ 裂缝的形成和扩展 在拉应力作用下，混凝土沿应力的垂直方向发生裂缝。 在压应力作用下，混凝土大致沿应力平行方向发生纵向劈裂裂缝，穿过粗骨料界面和砂浆内部。 在应力的下降过程中，变形仍继续增长，卸载后大部分变形不能恢复。 后两部分变形成分，不与混凝土的应力成比例变化，且卸载后大部分不能恢复，一般统称为 塑性变形 。 不同原材料和组成的混凝土，在不同的应力水平下，这三部分变形所占比例有很大变化。 ① 当混凝土应力较低时，骨料弹性变形占主要部分，总变形很小 ； ② 随应力的增 大，水泥凝胶体的粘性流动变形逐渐加速增长 ； ③ 接近混凝土极限强度时，裂缝的变形才明显显露，但其数量级大，很快就超过其它变形成分 。 在应力峰值之后，随着应力的下降，骨料弹性变形开始恢复，凝胶体的流动减小，而裂缝的变形却继续加大。 3. 应力状态和途径对力学性能的巨大影响 混凝土的单轴抗拉和抗压强度的比值约为 1:10 ，相应的峰值应变之比约为 1:20 ，都相差一个数量级。两者的破坏形态也有根本区别。 混凝土在基本受力状态下力学性能的巨大差别使得： ① 混凝土在不同应力状态下的多轴强度、变形和破坏形态等有很大的变化范围 ； ② 存在横向和纵向应力（变）梯度的情况下，混凝土的强度和变形值又将变化 ； ③ 荷载（应力）的重复加卸和反复作用下，混凝土将产生程度不等的变形滞后、刚度退化和残余变形等现象 ； ④ 多轴应力的不同作用途径，改变了微裂缝的发展状况和相互约束条件，混凝土出现不同力学性能反应 。 混凝土成熟度的增加，表示了水泥和骨料的粘结强度增大，水泥凝胶体稠化，粘性流动变形减小，因而混凝土的极限强度和弹性模量值都逐渐提高。但是，混凝土在应力的持续作用下，因水泥凝胶体的粘性流动和内部微裂缝的开展而产生的徐变与时俱增，使混凝土材料和构件的变形加大，长期强度降低。 混凝土周围的环境条件既影响其成熟度的发展过程，又与混凝土材料发生物理的和化学的作用，对其性能产生有利的或不利的影响。 4. 时间和环境条件的影响 混凝土随水泥水化作用的发展而渐趋成熟。有试验表明，水泥颗粒的水化作用由表及里逐渐深入，至龄期 20 年后仍未终止。 混凝土的这些材性特点，决定了其力学性能的复杂、多变和离散，同时由于混凝土原材料的性质和组成的差别很大，完全从微观的定量分析来解决混凝土的性能问题，得到准确而实用的结果是十分困难的。 所以，从结构工程的观点出发，将一定尺度，（例如 ≥ 70mm 或 3 ～ 4 倍粗骨料粒径）的混凝土体积作为单元，看成是连续的、匀质的和等向的材料，取其平均的强度、变形值和宏观的破坏形态等作为研究的标准，可以有相对稳定的力学性能．并且用同样尺度的标准试件测定各项性能指标。 混凝土在结构中主要用作受压材料， 最简单的单轴受压状态下的破坏过程最有代表性 。 混凝土一直被认为是“脆性”，材料，无论是受压还是受拉状态，它的破坏过程都短暂、急骤，肉眼不可能仔细地观察到其内部的破坏过程。现代科学技术的高度发展，为材料和结构试验提供了先进的加载和量测手段。现在已经可以比较容易地获得混凝土受压和受拉的应力 - 应变全曲线，还可采用超声波检测仪、 x 光摄影仪、电子显微镜等多种精密侧试仪器，对混凝土的微观构造在受力过程中的变化情况加以详尽的研究。 二 . 混凝土的变形及破坏机理 试验证明，结构混凝土在承受荷载或外应力之前，内部就已经存在少量、分散的微裂缝，宽（ 2-5 ） ×10 -3 、最长（ 1-2mm ）， 其主要原因是在混凝土的凝固过程中，粗骨料和水泥砂浆的收缩差和不均匀温湿度场所产生的微观应力场。由于水泥砂浆和粗骨料表面的粘结强度只及该砂浆抗拉强度的 35% ～ 65% ，而粗骨料本身的抗拉强度远超过水泥砂浆的强度，故当混凝土内微观拉应力较大时， 首先在粗骨料界面出现微裂缝，称界面粘结裂缝。 试验采用方形板式试件，既接近理想的平面应力状态，又便于在加载过程中直接获得裂缝的 x 光信息。 试验证实了混凝土在受力前就存在初始微裂缝，都出现在较大粗骨料的界面．开始受力后直到极限荷载，混凝土内的微裂缝逐渐增多和扩展，可以分作 3 个阶段： 粘结裂缝 σ=0 用 X 光观测的混凝土单轴受压的裂缝过程 1. 微裂缝相对称定期 (σ/σ max <0.3 ～ 0.5) 这时混凝土的压应力较小，虽然有些微裂缝的尖端因应力集中而沿界面略有发展，也有些微裂缝和间隙因受压而有些闭合，对混凝土的宏观变形性能无明显变化。 即使荷载的多次重复作用或者持续较长时间，微裂缝也不致有大发展，残余变形很小。 用 X 光观测的混凝土单轴受压的裂缝过程 σ=0.65σ max 2. 稳定裂缝发展期（ σ/σ max <0.75 ～ 0.9 ） 混凝土的应力增大后，原有的粗骨料界面裂缝逐渐延伸和增宽，其它骨料界面又出现新的粘结裂缝。界面裂缝逐渐地进入水泥砂浆，或者水泥砂浆中原有缝隙处的应力集力将砂浆拉断，产生少量微裂缝。但是， 当荷载不再增大，微裂缝的发展亦将停滞，裂缝形态保持基本稳定。 故荷载长期作用下，混凝土的变形将增大，但不会提前过早破坏。 σ=0.85σ max 用 X 光观测的混凝土单轴受压的裂缝过程 3. 不稳定裂缝发展期（ σ/σ max >0. 75 ～ 0. 9 ） 混凝土在高应力作用下，粗骨料的界面裂缝突然加宽和延伸；水泥砂浆中的已有裂缝也加快发展，并和相邻的粗骨料界面裂缝相连。这些裂缝逐个连通，构成大致平行于压应力方向的连续裂缝，或称纵向劈裂裂缝。 若混凝土中部分粗骨料的强度较低，或有节理和缺陷，也可能在高应力下发生骨料劈裂。 特点：应力增量不大，而裂缝发展迅速，变形增长大。即使应力维持常值，裂缝仍将继续发展，不再能保持稳定状态。 σ max 用 X 光观测的混凝土单轴受压的裂缝过程 从对混凝土受压过程的微观现象的分析，其破坏机理可以概括为： ⑴首先是水泥砂浆沿粗骨料的界面和砂浆内部形成微裂缝 ； ⑵应力增大后这些微裂缝逐渐地延伸和扩展，并连通成为宏观裂缝 ； ⑶砂浆的损伤不断积累，切断了和骨料的联系，混凝土的整体性遭受破坏而逐渐地丧失承载力 。 混凝土的强度远低于粗骨料本身的强度，当混凝土破坏后，其中的粗骨料一般无破损的迹象，裂缝和破碎都发生在水泥砂浆内部。所以，混凝土的强度和变形性能在很大程度上取决于水泥砂浆的质量和密实性。 任何改进和提高水泥砂浆质 量 的措施都能较多地提高混凝土强度和改善结构的性能。 0 2 4 6 8 10 20 30 s (MPa) e × 10 -3 B A C D A 点以前 ，微裂缝没有明显发展，混凝土的变形主要弹性变形。 A 点应力随混凝土强度的提高而增加，对普通强度混凝土 s A 约为 (0.3~0.4) f c ，对高强混凝土 s A 可达 (0.5~0.7) f c 。 A 点以后 ，裂缝开始有所延伸发展，产生部分塑性变形。微裂缝的发展导致混凝土的横向变形增加。但该阶段微裂缝的发展是稳定的。 典型的砼受压应力 - 应变曲线 随应变增长，试件上相继出现多条不连续的纵向裂缝，横向变形急剧发展，承载力明显下降，混凝土骨料与砂浆的粘结不断遭到破，裂缝连通形成斜向破坏面。 D 点的应变 e = (2~3) e 0 ，应力 s 等于 0.4 f c 左右。 达到 B 点，内部一些微裂缝相互连通，裂缝发展已不稳定，横向变形突然增大，体积应变开始由压缩转为增加。在此应力的长期作用下，裂缝会持续发展最终导致破坏。取 B 点的应力作为混凝土的长期抗压强度。普通强度混凝土 s B 约为 0.8 f c ，高强强度混凝土 s B 可达 0.95 f c 以上。 达到 C 点 f c ，内部微裂缝连通形成破坏面，应变增长速度明显加快， C 点的纵向应变值称为峰值应变 e 0 ，约为 0.002 。 三、影响应力 - 应变曲线形状的因素 1. 试验方法 在棱柱体抗压试验时，若应用普通液压式材料试验机加载，可毫无困难地获得应力应变曲线的上升段．但试件在达到最大承载力后急速破裂，量测不到有效的下降段曲线。 Whitney 很早就指出 混凝土试件突然破坏的原因是试验机的刚度不足 。 试验机本身在加载过程中发生变形，储存了很大的弹性应变能。当试件承载力突然下降时，试验机因受力减小而恢复变形，即刻释放能量，将试件急速压坏。 要获得稳定的应力 - 应变全曲线，主要是曲线的下降段，必须控制混凝土试件缓慢地变形和破坏。有两类试验方法： ①应用电液伺服阀控制的刚性试验机直接进行试件等应变速度加载； ②在普通液压试验机上附加刚性元件，使试验装置的总体刚度超过试件下降段的最大线刚度，就可防止混凝土的急速破坏。 按上述方法实测的混凝土棱柱体受压应力 - 应变全曲线如图。 加载中应变速率对应力 - 应变曲线的影响 不同强度混凝土的应力 - 应变关系曲线 强度等级越高，线弹性段越长，峰值应变也有所增大。但高强混凝土中，砂浆与骨料的粘结很强，密实性好，微裂缝很少，最后的破坏往往是骨料破坏，破坏时脆性越显著，下降段越陡。 2. 砼强度等级的影响 应变梯度对混凝土的强度和变形性能的影响。试验按照控制截面应变方法的不同分作三类 1. 等偏心距试验 ( e 0 =const) 按预定偏心距确定荷载位置，一次加载直至试件破坏为止。试件的截面应变随荷载的增大而变化，应变梯度逐渐增大，中和轴因混凝土受压的塑性变形等原因而向荷载方向有少量移动。 3. 应变梯度的影响 3. 等应变梯度加载（ ε 1 -ε 2 =const ） 试件由试验机施加轴力 N ，在横向有千斤顶施加弯矩 M 。试验时按预定应变梯度同时控制 N 和 M ，使截面应变平行地增大，应变梯度保持为一常值。 2. 全截面受压，一侧应变为零（ ε 2 ≡o) 截面中心的主要压力 (N 1 ）由试验机施加。偏心压力（ N 2 ）由液压千斤顶施加，数值可调，使一侧应变为零。截面应变分布始终成三角形，但应变梯度渐增。 2.2.2 主要试验结果 1. 极限承载力（ N p ）和相应的最大应变 (ε 1p ) 试件破坏时的极限承载力随荷载偏心距（ e o ）的增大而降低，但是均明显高出按线性应力图（弹性）计算的承载力： 表明混凝土塑性变形产生的截面非线性应力分布，有利于承载力的提高。 在极限荷载下，试件截面的最大压应变 (ε 1p ) 达 3.0 ～ 3.5 × 10 -3 ，随偏心距的变化并不大。此应变值显著大于混凝土轴心受压的峰值应变 ε p ，说明试件此时的最外纤维已进入应力 - 应变曲线的下降段。 应力 - 应变关系 在混凝土棱柱体的偏心受压试验中，虽然可以准确地确定荷载的数值和位置，并量测到截面的应变值和分布，但由于混凝土应力 - 应变的非线性关系，截面的应力分布和数值仍不得而知。故偏心受压情况下的混凝土应力 - 应变全曲线不能直接用试验数据绘制。为了求得混凝土的偏心受压应力 - 应变全曲线，只能采取一些假定，推导基本计算公式，并引人试验数据进行大量的运算。现有计算方法分两类： ⑴ 增量方程计算法。将加载过程划分成多个微段，用各荷载段的数据增量代入基本公式计算一一对应的应力和应变关系，作图相连得应力 - 应变全曲线； ⑵给定全曲线方程，拟合参数值。首先选定合理的全曲线数学方程，用最小二乘法作回归分析，确定式中的参数值。 根据试验结果和分析，过镇海建议采用混凝土偏心抗压强度（ f c.e ）和相应峰值应变 (ε p,e ) 随偏心距 (e 0 ）而变化的简化计算式 理论曲线和试验结果的比较如图。 按上式计算，轴心受压构件（ e 0 =0) 得 1 ，受弯构件 (e 0 ＝∞ ) 得 1.2 。 偏心受压的抗压强度 4. 侧向约束的影响 侧向受约束时混凝土的变形特点  cu 约束混凝土 非约束混凝土  c  c f cc f c E sec E c  c0 2  c0  sp  cc o 环箍断裂 受压应力 - 应变全曲线 混凝土受压应力 - 应变全曲线包括上升段和下降段，是其力学性能的全面宏观反应： ◆ 曲线峰点处的最大应力即棱柱体抗压强度，相应的应变为峰值应变 ε p ； ◆曲线的（割线或切线）斜率为其弹性（变形）模量，初始斜率即初始弹性模量 E c ； ◆下降段表明其峰值应力后的残余强度；曲线的形状和曲线下的面积反映了其塑性变形的能力，等等。 全曲线方程 绘制峰值点坐标为（ 1 ， 1 ）的标准曲线如图，曲线形状有一定差别，但具有一致的几何特性，可用数学条件描述。 混凝土受压应力 - 应变全曲线、及图像化的本构关系，是研究和分析混凝土结构和构件受力性能的主要依据，为此需要建立相应的数学模型。 将混凝土受压应力 - 应变全曲线用无量纲坐标表示： 其几何特征的数学描述如下： 这些几何特征与混凝土的受压变形和破坏过程（见前）完全对应．具有明确的物理意义。 下降段曲线可无限延长，收敛与横坐标轴，但不相交； 为了准确地拟合混凝土的受压应力 - 应变试验曲线，各国研究人员提出了多种数学函数形式的曲线方程，如：多项式、指数式、三角函数、有理分式、分段式等等。 对于曲线的上升段和下降段，有的用统一方程，有的则给出分段公式。其中比较简单、实用的曲线形式如图。 清华大学研究组建议及 《 规范 》 所采用的分段式曲线方程为： 其中上升段⑴式应满足数学条件描述中 1 、 2 、 3 、 7 ，下降段⑵式应满足数学条件描述中的 3 ～ 7 。 ⑴ ⑵ 将条件 1 和 3 中的三个边界条件代入⑴式，可解得： 式中还有一个独立参数 a 1 。从式⑴可知，当 x =0 时，有 dy / dx = a 1 从各符号的定义可得： 符合曲线在峰点连续的条件。 式中： 混凝土的初始切线弹性模量（ N/mm 2 ）。 混凝土棱柱体抗压强度和峰值应变的比值，即峰值割线模量（ N/mm 2 ）。 α a = a 1 ，规范称之为曲线上升段参数。 物理意义：混凝土的初始切线模量与峰值割线模量之比 E 0 /E p ； 几何意义：曲线的初始斜率和峰点割线斜率之比。 上升段曲线方程为： 上升段曲线方程，满足数学条件描述 7 。由条件 2 的不等式，可得 α a 值的范围： ⑶ 上升段理论曲线随参数 α a 的变化： α a ＞ 3 ，曲线局部 y ＞ 1 ， 显然违背试验结果； 1.1 ＜ α a ＜ 1.5 ， 曲线的初始段（ x ＜0 .3 ）内有拐点，单曲度不明显，在 y≤0.5 ～ 0.6 范围内接近一直线； α a ＜ 1.1 ， 上升段曲线上拐点明显，与混凝土材性不符。 下降段曲线方程中包含三个参数，将数学条件描述中 3 的两个边界条件代入，可解得： 式中 b 0 为独立参数，在混凝土规范中称为下降段参数， 即 α d = b 0 ， 将其代入上式，并化简可得： 上式满足数学条件描述中的 6 、 7 。 可解得拐点位置 x D （＞ 1.0 ） 此外，由数学条件 4 满足： 同理，由数学条件 5 满足： 可解得最大曲率点的位置 x E （＞ x D ） 下降段曲线上两个特征点 D 、 E 的位置随参数 α d 值而变化， 计算结果如图，与试验数据一致。 对参数取 α a 和 α d 赋 予不等的数值，可得变化的理论曲线。 对于不同原材料和强度等级的结构混凝土，甚至是约束混凝土，选用了合适的参数值。都可以得到与试验结果相符的理论曲线。过镇海等建议的参数值见表，可供结构分析和设计应用。 规范中的曲线方程和参数值 1 、用于非线性分析 混凝土结构设计规范附录 C 中，建议采用的混凝土单轴（即轴心）受压应力 - 应变全曲线方程同前： 但式中的纵、横坐标改为： 式中： f c ＊ — 混凝土的单轴（即轴心）抗压强度（ N/mm 2 ），应根据结构分析方法和极限状态验算的需要，分别取为标准值（ f ck ）、设计值（ f c ）或平均值（ f cm ）； ε c — 与 f c ＊ 相应的峰值压应变。 ε c 按下式计算： 上升段和下降段的曲线参数分别按下式计算： 在应力 - 应变曲线的下降段上，当应力（残余强度）减至 0.5 f c ＊ 时，所对应的压应变为 ε u 。其值可由 解得： 分析或验算结构构件时，混凝土的单轴压应变不宜超过值 ε u 。 ⑷ 按上述公式计算随混凝土抗压强度而变化的各项参数值，经整理后如表。 将这些参数带入式⑶、⑷即得混凝土单轴（轴心）受压应力 - 应变全曲线。 1.8 1.8 1.9 1.9 2.0 2.1 2.3 2.6 3.0 4.2 3.00 2.74 2.48 2.21 1.94 1.65 1.36 1.06 0.74 0.41 1.65 1.71 1.78 1.84 1.90 1.96 2.03 2.09 2.15 2.21 2030 1980 1920 1850 1790 1720 1640 1560 1470 1370 60 55 50 45 40 35 30 25 20 15 混凝土单轴受压应力 - 应变曲线的参数值 混凝土结构设计规范附录 C 明确指出，上述公式的适用条件是：混凝土强度等级 C15 ～ C80 ，质量密度（ 2200 ～ 2400 ） kg/m 3 ，正常温、湿度环境和加载速度等。当结构或构件的受力状态或环境条件不符合此要求时，例如混凝土受有横向和纵向应变梯度、箍筋约束作用、重复加卸载、持续荷载或快速加载，高温作用、 … … 等因素的影响时，应对应力 - 应变曲线方程的各参数值进行适当修正。 2 、用于构件正截面承载力计算 钢筋混凝土和预应力混凝土的受弯构件、偏心受压构件和大偏心受拉构件等，在内力作用下截面上将出现沿局部或全截面的不均匀压应力分布。在计算这类构件的正截面极限承载力时，混凝土规范所采用的基本假定中，规定了混凝土受压应力 - 应变曲线方程为： 上升段： 下降段： ≯2.0 ≮ 0.002 ≯0.0033 取 曲线方程可改写为 式中各参数都随混凝土的立方体抗压强度标准值 f cu,k 而变化，计算公式为： 《 规范 》 混凝土应力 - 应变曲线参数 f cu ≤ C50 C60 C70 C80 n 2 1.833 1.667 1.5 e 0 0.002 0.00205 0.0021 0.00215 e u 0.0033 0.0032 0.0031 0.003 上升段： 下降段： 按上述方程计算的不同强度等级混凝土的受压应力 - 应变曲线的各参数值列如下表，各理论曲线如图。 ≯2.0 ≮ 0.002 ≯0.0033 比较 计算正截面承载力时所采用的受压应力 - 应变曲线与棱柱体受压试验所得曲线存在显著差异： ⑶ ⑷ ⑴ 按式 混凝土达 抗压强度后，应力保持不变，为一水平线，应变值不超过 ε cu ，但始终不出现下降段。 ⑵与抗压强度相应的压应变值 ε 0 均大于棱柱体的受压峰值应变 ε c 。 ⑶上升段曲线的形状稍有不同，式中的参数 n 和参数 α a 具有相同的几何意义： ⑶ 上升段曲线的形状稍有不同，式中的参数 n 和参数 α a 具有相同的几何意义： 同为曲线的初始斜率。 这些差别说明：计算正截面承载力所采用的混凝土受压应力 - 应变曲线比棱柱体轴心受压的相应曲线更丰满、峰值应变更大、曲线下的面积更大。这里考虑了实际工程中的结构构件一般都具有应变梯度、箍筋约束、龄期较长等有利因素，因而作出相应的修正。按此计算构件的正截面极限承载力与试验结构更相符，但并不适用于结构构件受力全过程的非线性分析。 Hognestad 建议的应力 - 应变曲线 Rüsch 建议的应力 - 应变曲线 0 0.002 0.0033 f c s e e 0 e cu