室内设计工程制图ppt课件 66页

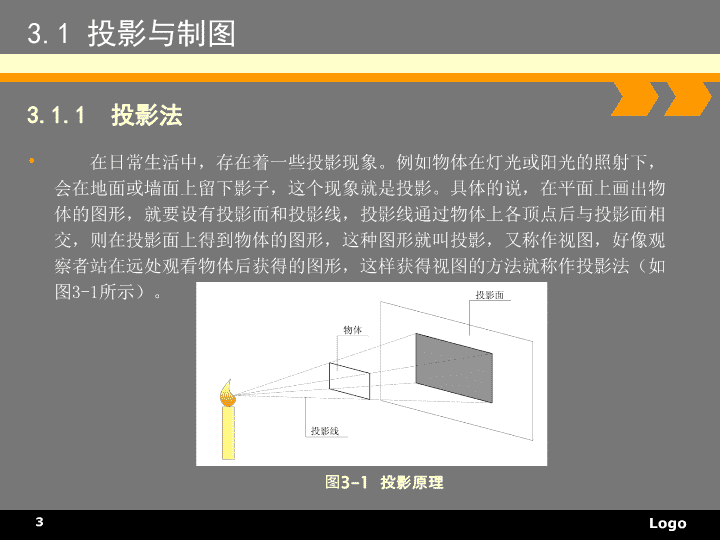
第三章制图投影绘制室内设计工程制图1nLogo3.1投影与制图目录13.2三面投影图及其对应关系233.3点、直线、平面的投影43.4体的投影2nLogo在日常生活中，存在着一些投影现象。例如物体在灯光或阳光的照射下，会在地面或墙面上留下影子，这个现象就是投影。具体的说，在平面上画出物体的图形，就要设有投影面和投影线，投影线通过物体上各顶点后与投影面相交，则在投影面上得到物体的图形，这种图形就叫投影，又称作视图，好像观察者站在远处观看物体后获得的图形，这样获得视图的方法就称作投影法（如图3-1所示）。3.1投影与制图3.1.1投影法图3-1投影原理3nLogoLogo图3-2中心投影法3.1投影与制图1．中心投影法所有的投射线都交于投影中心的投影方法称为中心投影法。如图3-2所示，设S点为一白炽灯的发光点。自S发出无数光线，经三角板三个顶点A、B、C三条投影线，延长与投影面（H）相交得三个点a、b、c，三角形abc为三角板的投影。这种投影的形式被称为中心投影法。中心投影法不能反映出物体的真实形状和大小，并且会随着物体的位置变化而变化。中心投影法常用语透视图中，不能作为工程图。3.1.2投影法的分类4nLogoLogoLogo图3-1绘图版与丁字尺的用法3.1投影与制图在日常生活中，存在着一些投影现象。例如物体在灯光或阳光的照射下，会在地面或墙面上留下影子，这个现象就是投影。具体的说，在平面上画出物体的图形，就要设有投影面和投影线，投影线通过物体上各顶点后与投影面相交，则在投影面上得到物体的图形，这种图形就叫投影，又称作视图，好像观察者站在远处观看物体后获得的图形，这样获得视图的方法就称作投影法（如图3-1所示）。3.1.2投影法5nLogoLogoLogo图3-3正投影法3.1投影与制图2．平行投影法所有的投影线相互平行的投影方法叫平行投影法，如太阳离地球较远，所照射出的光线可作为平行光线，所得的投影称为平行投影。根据投影线是否与投影面垂直，平行投影法又分为正投影法和斜投影法。1）正投影——投影线垂至于投影面称为正投影法，所得的投影△abc称为正投影，如图3-3所示。6nLogoLogoLogo图3-4斜投影法3.1投影与制图2）斜投影——投影线与投影面倾斜的平行投影法称为斜投影法，所得的投影△abc称为斜投影。斜投影法一般用于轴测图的绘制，能表现物体的立体形象和尺寸，如图3-4所示。7nLogoLogoLogo图3-5物体的单个方向投影3.2三面投影图（三视图）及其对应关系用正投影法绘制出的图形称作视图。用正投影法绘制物体视图时，是将物体放在绘图者和投影面之间，以观察者的视线作为互相平行的投影线，将观察到的物体形状画在投影面上。如图3-5所示，几个形状不同的物体在同一个投影面上的投影是相同的，因此，物体的一个视图不能反映出物体的真实形态，需要有其他方向的投影，才能清楚完整的反映出物体的全貌。为此，我们设置三个互相垂直的平面作为投影面来表达物体的形状。3.2.1三面视图的形成8nLogoLogoLogoLogo图3-6三个方向投影面体系3.2三面投影图（三视图）及其对应关系原来的投影面H，称为水平投影面，简称平面；增设一V面，称为正立投影面，简称正面；和垂直于H、V两个面的W面,称为侧立投影面，简称侧面（如图3-6所示）。9nLogoLogoLogoLogoLogo图3-7三视图形成3.2三面投影图（三视图）及其对应关系三个投影面形成三个体系，出现三个投影轴OX、OY、OZ，并且相互垂直交于一点O，称为原点。在三个体系中放置一个物体，使其主要面平行于投影面，用正投影法在H、V、W面中得到三个投影，称三视图，如图3-7所示。主视图：又称作正立面图，在V面上得到的投影图，由前向后投影；俯视图：又称作平面图，在水平面H上的到的投影图，由上向下投影；左视图：又称作侧立面图，在W面上得到的投影图，由左向右投影。10nLogoLogoLogoLogo图3-8三个投影面展开3.2三面投影图（三视图）及其对应关系展开时，正面V保持不动，H面按OX轴向下旋转90°；W面绕OZ轴向右旋转90°，使三个投影面展开（如图3-8至图3-9所示）。为了作图方便，可做一条45°的辅助线反应平面图与侧面图的对应关系。3.2.2三面视图的展开图3-9三个投影面展开后视图11nLogoLogoLogoLogoLogo3.2三面投影图（三视图）及其对应关系1．三面视图的位置关系平面图在正立面图的下方，左立面图在正立面图的右侧，三个视图位置不发生改变。2．三面视图的三等关系三视图是由同一物体、同一位置情况下，进行的三个不同方向的正投影得到的，因此各个视图间存在着严格的尺寸关系。如图3-10所示，正面视图和平面图的长度相等并对正；正面图和侧面图中的高度相等并且平齐；平面图、侧面图中的宽度相等。总结起来就是：长对正、高平齐、宽相等。3.2.3三面视图的对应关系12nLogo图3-10三个视图的尺寸关系3.2三面投影图（三视图）及其对应关系13nLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影假设空间有A点，将其放在三个投影体系中，自A点分别向三个投影面做垂线，获得点的三个投影。空间点为A，在H面的投影用小写字母a表示，V面投影用a′表示,W面投影用a″表示，如图3-11所示。3.3.1点的投影图3-11点的三面投影14nLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影再将三块投影面展开后摊平，在每一个投影平面内，都可表现出A点的投影图形，如图3-12所示。点的投影图特征：1）点的正面投影和水平投影的连线，在同一垂直线上；2）点的正面投影和侧面投影的连线，在同一水平线上；3）点的水平投影到OX轴的距离，等于该点的侧面投影到OZ轴的距离,反映空间点到V面的距离（同理，空间点到H和W面的距离也可以从点的正面、水平投影中得到反映）。图3-12点的投影15nLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影1．直线实长的投影图特征：直线对一个投影面相对位置有平行、垂直、倾斜三种，如图3-13所示。直线平行于一个投影面，该直线叫做“投影面平行线”。直线垂直于一个投影面，该直线叫做“投影面垂直线”。直线倾斜投影面，该直线对投影面既不平行也不垂直，该直线叫做“一般位置直线”。3.3.2点的投影（1）平行（2）垂直（3）倾斜图3-13直线的投影16nLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影2．直线在三面体系中的投影1）投影面平行线如图3-14所示，直线平行于投影面有三种形式：水平线:平行于H面，与V、W面倾斜的直线，如图3-14中的直线AB；（a）直线AB位置图（b）直线AB投影图图3-14直线AB平行于H面17nLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影正平线:平行于V面，与H、W面倾斜的直线，如图3-15中的直线AB；（a）直线AB位置图（b）直线AB投影图图3-15直线AB平行于V面18nLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影侧平线:平行于W面，与H、V面倾斜的直线，如图3-16中的直线AB。（a）直线AB位置图（b）直线AB投影图图3-16直线AB平行于W面19nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影2）投影面垂直线，直线平行于投影面有三种形式：铅垂线：垂直于H面的直线，如图3-17中的直线AB；（a）直线AB位置图（b）直线AB投影图图3-17直线AB垂直与H面20nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影正垂线：垂直于V面的直线，如图3-18中的直线AB；（a）直线AB位置图（b）直线AB投影图图3-18直线AB垂直与V面21nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影侧垂线：垂直于W面的直线，如图3-19中的直线AB。（a）直线AB位置图（b）直线AB投影图图3-19直线AB垂直与W面22nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影3）一般位置投影如图3-20所示，直线AB与H、V、W三个投影面都倾斜，因此，他在三个投影面上的长度都要变短。（a）直线AB位置图（b）直线AB投影图图3-20直线AB与H、V、W三个面倾斜23nLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影平面对一个投影面相对位置有三种情况：平行、垂直、倾斜三种（如图3-21所示）。平行于一个投影面，并且垂直于另两个投影面的平面，叫做“投影面平行面”。如果平面内有一根直线，垂直于一个投影面，并且与另外两个投影面倾斜的平面，叫做“投影面垂直面”在三个投影面体系中，不平行同时也不垂直于任何一个投影面的平面，叫做“一般位置平面”。3.3.3平面的投影（1）平行面（2）垂直（3）倾斜图3-21面的投影24nLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影1．投影面平行面1）平面在它所平行的投影面上的投影，反映实形；2）该平面的另外两面投影，各积聚成一条直线，且平行于相应的投影轴（如图3-22所示）。（a）面ABCD位置图（b）面ABCD投影图图3-22投影面平行面25nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影2．投影面垂直面1）空间平面在它所垂直的投影面上的投影，积聚成一条直线；2）空间平面在它所不垂直，同时也不平行的投影面上的投影，仍为平面图形，但小于原来空间平面图形（如图3-23所示）。（a）面ABCD位置图（b）面ABCD投影图图3-23投影面垂直面26nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.3点、直线、平面的投影3．一般位置平面一般位置平面的投影特征：1）一般位置平面在任一投影面的投影，均不反映该平面的空间实形；2）在任一投影面上的投影，均无积聚性（如图3-24所示）。（a）面ABCD位置图（b）面ABCD投影图图3-24投影面一般位置平面27nLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1．六棱柱的投影如图3-25所示为一正六棱柱，由上、下两底面（正六边形）和六个等大棱面（长方形）组成。并将其放置成上、下底面与水平投影面H平行，并有两个棱面平行于正投影面V（如图3-26所示）。3.4.1平面体的投影图3-25六棱柱示意图图3-26六棱柱位置图28nLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影作图方法与步骤a、作正六棱柱的对称中心线和底面基线，画出具有形状特征的投影——水平投影。b、根据投影三等关系（长对正、高平齐、宽相等）作出其他两个投影（如图3-27所示）。从图3-26可以看出当棱柱的底面平行某一个投影面时，则棱柱在该投影面上投影的外轮廓为与其底面全等的正多边形，而另外两个投影则由若干个相邻的矩形线框所组成。图3-27六棱柱投影图29nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影棱柱表面上点的投影如图3-26所示，已知棱柱表面上点E的正面投影e′，求作它的其他两面投影e、e″。因为棱面ABCD是铅垂面，在H面上的投影有积聚性。因此，在图中自e′做垂线，与ab(c)(d)交于点e,即e点为棱面ABCD上E点的水平投影；再根据e、e′可求出e″（如图3-28所示）。图3-28六棱柱表面上点的投影图30nLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1．棱锥的投影如图3-29所示为一正三棱锥，它的表面由一个底面（正三边形ABC）和三个侧棱面（等腰三角形）围成，将其放置成底面△ABC与水平投影面H平行，并有一个棱面垂直于侧投影面（如图3-30所示）。图3-29三棱锥示意图图3-30三棱锥位置图31nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影作图方法与步骤a、作正三棱锥的对称中心线和底面基线，画出底面△ABC水平投影的等边三角形△abc。b、根据正三棱锥的高度定出锥顶S的投影位置s′，然后在正面投影和水平投影上用直线连接锥顶与底面四个顶点的投影，即得四条棱线的投影。c、根据投影规律，由正面投影和水平投影作出侧面投影（如图3-31所示）。从图3-30中可以看出当棱锥的底面平行某一个投影面时，则棱锥在该投影面上投影的外轮廓为与其底面全等的正多边形，而另外两个投影则由若干个相邻的三角形线框所组成。图3-31三棱锥投影图32nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影棱锥表面点的投影棱锥表面有两个点：E为可见点，F为不可见点。如图3-30所示，因为点E在△SAB上为可见，△SAB是一般位置平面，通过做辅助线，过点E及锥顶点S作一条直线SD，与底边AB交于点D。即过e′作s′d′，再作出其水平投影sd。由于点E属于直线SD，根据点在直线上的从属性质可知e必在sd上，求出水平投影e，再根据e、e′可求出e″。如图3-33所示，因为点F不可见，故点F必定在棱面△SAC上。棱面△SAC为侧垂面，它的侧面投影积聚为直线段s″a″（c″），因此f″必在s″a″（c″）上，由f、f″即可求出f′。图3-32三棱锥表面可见点投影图33nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影棱锥表面点的投影棱锥表面有两个点：E为可见点，F为不可见点。如图3-30所示，因为点E在△SAB上为可见，△SAB是一般位置平面，通过做辅助线，过点E及锥顶点S作一条直线SD，与底边AB交于点D。即过e′作s′d′，再作出其水平投影sd。由于点E属于直线SD，根据点在直线上的从属性质可知e必在sd上，求出水平投影e，再根据e、e′可求出e″。如图3-33所示，因为点F不可见，故点F必定在棱面△SAC上。棱面△SAC为侧垂面，它的侧面投影积聚为直线段s″a″（c″），因此f″必在s″a″（c″）上，由f、f″即可求出f′。图3-33三棱锥表面不可见点投影图34nLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1．圆柱的投影如3-34所示，圆柱面可看作一条母线AA1围绕与它平行的轴线OO1回转而成。AA1叫做母线，圆柱面上任意一条平行于轴线的直线，称为素线。并且为了方便作图，一般将它的轴线垂直于某个投影面（如图3-35所示）。3.4.2曲面体的投影图3-34圆柱示意图图3-35圆柱位置图35nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影作图方法与步骤a、作侧面投影的中心线和轴线的正面投影和水平投影（点划线）b、作侧面投影的圆形。c、根据圆柱的高度，按投影规律（长对正、高平齐、宽相等），作出正面投影和水平投影（如图3-36所示）。从图3-35中可以看出当圆柱的轴线垂直某一个投影面时，必有一个投影为圆形，另外两个投影为全等的矩形。图3-36圆柱投影图36nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影圆柱表面上点的投影如图3-35所示，已知圆柱面上点M的正面投影m′，求作点m和m″。因为圆柱面的侧面投影积聚成一个圆，因而圆柱面上的M点其侧面投影m一定在圆柱面的侧面投影圆周上。又因为m′可见，因此由m′和m，可求得m″（如图3-37所示）。图3-337圆柱表面上点的投影图37nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1．圆锥的投影圆锥面可看作是一条直母线SA围绕与它平行的轴线SO回转而成。在圆锥面上通过锥顶的任一直线称为圆锥面的素线。母线上任意一点M随母线旋转的轨迹均是圆，这些圆被称为纬圆（如图3-38所示）。图3-38圆锥示意图图3-35圆锥位置图38nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影作图方法与步骤a、作水平投影的中心线和轴线的正面投影和水平投影。b、作水平投影的圆形。c、根据圆锥的高度定出锥顶S的投影位置，然后根据投影规律（长对正、高平齐、宽相等），作出正面投影和水平投影，其投影图如图3-40所示。从图3-40中可以看出，当圆锥的轴线垂直某一个投影面时，则圆锥在该投影面上投影为与其底面全等的圆形，另外两个投影为全等的等腰三角形。图3-40圆锥投影图39nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影圆锥表面上点的投影方法一：如图3-41（a）所示，过锥顶S和点M作一直线SA，与底面交于点A。点M的各个投影必在此SA的相应投影上。在图3-41（b）中过m′作s′a′，然后求出其水平投影sa。由于点M在直线SA上，根据点在直线上的从属性质可知m必在sa上，求出水平投影m，再根据m、m′可求出m″。图3-41（a)40nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影圆锥表面上点的投影方法一：如图3-41（a）所示，过锥顶S和点M作一直线SA，与底面交于点A。点M的各个投影必在此SA的相应投影上。在图3-41（b）中过m′作s′a′，然后求出其水平投影sa。由于点M在直线SA上，根据点在直线上的从属性质可知m必在sa上，求出水平投影m，再根据m、m′可求出m″。图3-41（b)41nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影方法二：如图3-42（a）所示，过圆锥面上点M作一个垂直于圆锥轴线的辅助圆，点M的各个投影必在此辅助圆的相应投影上。在图3-42(b)中过m′作水平线a′b′，此为辅助圆的正面投影积聚线。辅助圆的水平投影为一直径等于a′b′的圆，圆心为s，由m′向下引垂线与此圆相交，且根据点M的可见性，即可求出m。然后再由m′和m可求出m″。图3-42（a)42nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影方法二：如图3-42（a）所示，过圆锥面上点M作一个垂直于圆锥轴线的辅助圆，点M的各个投影必在此辅助圆的相应投影上。在图3-42(b)中过m′作水平线a′b′，此为辅助圆的正面投影积聚线。辅助圆的水平投影为一直径等于a′b′的圆，圆心为s，由m′向下引垂线与此圆相交，且根据点M的可见性，即可求出m。然后再由m′和m可求出m″。图3-42（b)43nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影3．球的投影如图3-44所示，圆球在三个投影面上的投影都是直径相等的圆，他们分别是这个球面的三面投影的转向轮廓线。正面投影的圆它是前面可见半球与后面不可见半球的分界线的投影。与此类似，侧面投影的圆是左半球与右半球的分界线的投影；水平投影的圆是平行于H面的上半球与下半球的分界线的投影，其投影图如图3-45所示。图3-43圆球示意图图3-44圆球位置图44nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影3．球的投影如图3-44所示，圆球在三个投影面上的投影都是直径相等的圆，他们分别是这个球面的三面投影的转向轮廓线。正面投影的圆它是前面可见半球与后面不可见半球的分界线的投影。与此类似，侧面投影的圆是左半球与右半球的分界线的投影；水平投影的圆是平行于H面的上半球与下半球的分界线的投影，其投影图如图3-45所示。图3-45圆球投影图45nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影圆球表面上点的投影如图3-46，已知球面上点A的正面投影a′，求作他的水平投影a和侧面投影a″。虽然球的三面投影都没有积聚性，并且球面上也不存在直线，但可以通过球面上的点A做平行于投影面的圆。现在，通过点A作水平圆，实际上这个圆为点A绕球的铅垂轴线旋转而成的。a、通过a′作这个圆的正面投影，按照在正面投影中所显示的这个圆的直径长度，做出反应这个圆实形的水平投影。b、由于a′可见，可由a′在这个圆的前半圆的水平投影上作出a。图3-46圆球表面上点的投影图46nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影圆球表面上点的投影如图3-46，已知球面上点A的正面投影a′，求作他的水平投影a和侧面投影a″。虽然球的三面投影都没有积聚性，并且球面上也不存在直线，但可以通过球面上的点A做平行于投影面的圆。现在，通过点A作水平圆，实际上这个圆为点A绕球的铅垂轴线旋转而成的。a、通过a′作这个圆的正面投影，按照在正面投影中所显示的这个圆的直径长度，做出反应这个圆实形的水平投影。b、由于a′可见，可由a′在这个圆的前半圆的水平投影上作出a。c、根据a′、a做a″，因为根据a′判断出，点A位于上半球和左半球上，所以a″是可见的。图3-46圆球表面上点的投影图47nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影由图3-47某高层建筑图可以知道，建筑是由多个几个形体组合而成的。常见的基本几何体有棱柱、棱锥、圆柱、圆锥、球等。3.4.3组合体的投影图3-47某高层建筑48nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1．组合体的形成方法组合体的形状一般比较复杂，假设把组合体分解，然后根据分解后的各个平面体、曲面体和他们的相对位置等进行分析，画清各部分的形状特征，这种分析方法称为形体分析法。必须注意的是，对建筑物或构建进行形体分解仅仅是一种假想的方法。需要注意的是，建筑是一个整体，是不可分割的。形体分析法仅是一种假想的分析方法。组合体的组合方式可以是叠加、相切和二者混合等多种形式。49nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1）叠加式把组合体看成由若干个基本形体叠加而成，如图3-48所示，该基础是由1、2、3、4四个平面几何体叠加而成。图3-48叠加式组合体50nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影2）切割式有些组合体可以看作是由一个大的基本形体经过若干次切割而成（如图3-49所示）。图3-49切割式组合体51nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影3）混合式组合体的分解是由叠加和切割这两种形式组成（如图3-50所示）。图3-50混合式组合体52nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影2．组合体的连接关系所谓连接关系，就是指基本形体组合成组合体时，各基本形体表面间真实的相互关系。组合体的表面连接关系主要有：两表面相互平齐、不平齐、相切、相交（如图3-51所示）。组合体的表面连接关系不同，投影图的画法也不同。53nLogo3.4体的投影（a）表面平齐，相交处不画线图3-51组合体的表面连接关系（b）表面不平齐，画线（c）表面相切，相切处不画线（d）表面相交，相交处画线54nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影3．组合体的投影图画法1）形体分析由图3-52可知，此图为切割型组合形式。图3-52组合体的投影图画法55nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影2）确定位置根据基础在房屋中的位置，形体应水平放置，使底面平行于水平投影面H，且在三视图中V视图为主视图，将反应物体主要特征的面平行于V面，并尽量保证尽量多的平面与投影面平行或垂直。3）确定视图数量视图的数量要尽量用少的数量把形体表现完整、清晰。该形体的主要形态由正面，顶面，侧面即可体现，因此需要画出V、H、W三面投影即可。56nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影4．组合体的尺寸标注常见几个形体的尺寸标注，一般只标注其长、宽、高或直径即可，如图3-53所示。图3-53常见几何体尺寸标注法57nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影4．组合体的尺寸标注常见几个形体的尺寸标注，一般只标注其长、宽、高或直径即可，如图3-53所示。图3-53常见几何体尺寸标注法58nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1）尺寸的种类a、细部尺寸：用于确定组合体中各基本体自身大小的尺寸（如图3-54至图3-55所示）。b、定位尺寸：用于确定组合体中各基本形体之间相互位置的尺寸。c、总体尺寸：确定组合体总长、总宽、总高的外包尺寸。图3-54组合体的尺寸标注59nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影1）尺寸的种类a、细部尺寸：用于确定组合体中各基本体自身大小的尺寸（如图3-54至图3-55所示）。b、定位尺寸：用于确定组合体中各基本形体之间相互位置的尺寸。c、总体尺寸：确定组合体总长、总宽、总高的外包尺寸。图3-54组合体的尺寸标注60nLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogoLogo3.4体的投影2）尺寸标注要求a、组合体尺寸标注前需进行形体分析，弄清反映在投影图上的有哪些基本形体，然后注意这些基本形体的尺寸标注要求，做到简洁合理。b、各基本形体之间的定位尺寸一定要先选好定位基准，再行标注，做到心中有数不遗漏。c、由于组合体形状变化多，定形、定位和总体尺寸有时可以相互兼代。d、组合体各项尺寸一般只标注一次。（3）尺寸标注中应注意的问题a、尺寸一般应布置在图形外，以免影响图形清晰。b、尺寸排列要注意大尺寸在外、小尺寸在内，并在不出现尺寸重复的前提下，使尺寸构成封闭的尺寸链。c、反映某一形体的尺寸，最好集中标在反映这一基本形体特征轮廓的投影图上。d、两投影图相关的尺寸，应尽量标注在两图之间，以便对照识读。e、尽量不在虚线图形上标注尺寸。具体标注方式见第四章4.1.5尺寸标注。61nLogoLogo本章小结：本章节重点在于培养学生的空间想象能力，即从二维德平面图想象出三维的立体形态，这是工程制图的一个难点。因为在今后进行的艺术设计创作中，需要经常不断的将头脑中想象的图形落实到图面上，再由图面制成立体的形态。所以，学生要在开始学习工程制图时，就培养、训练这种思维方式和绘图技巧，为学习专业设计课打下良好基础。课后习题：1.什么是投影？2．什么是投影现象？投影法有几种？3．正投影法中的点、直线、平面有哪些投影特征？4．三视图都有那些内容？5．三视图的对应关系是什么？62nLogo6．画出下图的三视图。7．组合体的形成方法？63nLogoLogoLogo8．画出下图的三视图，并标注出尺寸。64nThankyou室内设计工程制图65n此课件下载可自行编辑修改，供参考！感谢您的支持，我们努力做得更好！