2.4-流体运动的积分方程 41页

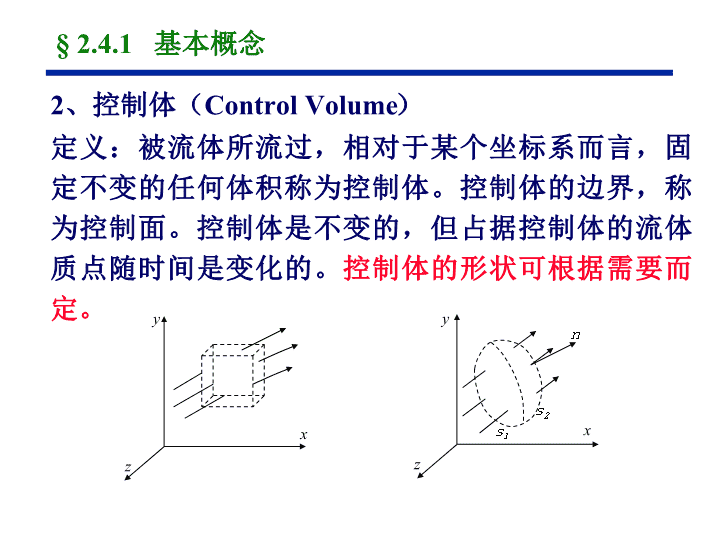
§2.4流体运动的积分方程§2.4.1基本概念流体动力学是研究产生流体运动的原因。为此，我们必须解决三个方面的问题：（1）流体的运动学问题（如前述）；（2）作用于流体上各种力的特征（如前述）；（3）控制流体运动的普遍规律；流体动力学基本方程就是将经典牛顿力学描述物质运动的普遍规律，应用于流体运动的物理现象中，从而得到联系流体运动各物理量之间的关系式。\n系统的基本特点：（1）系统边界随流体一起运动；（2）在系统的边界上没有质量的交换；（3）在系统的边界上受到外界的表面力；（4）在系统的边界上存在能量的交换。t’txyz§2.4.1基本概念1、系统(System)定义：系统是指包含着确定不变物质的任何集合体，称为系统。在流体力学中，系统是指由任何确定流体质点组成的团体。\n2、控制体（ControlVolume）定义：被流体所流过，相对于某个坐标系而言，固定不变的任何体积称为控制体。控制体的边界，称为控制面。控制体是不变的，但占据控制体的流体质点随时间是变化的。控制体的形状可根据需要而定。§2.4.1基本概念xzyxyzs1s2n\n控制体的基本特点:（1）控制体的边界相对于坐标系而言是固定的；（2）在控制面上可以发生质量交换，即流体可以流进、流出控制面；（3）在控制面上受到外界作用于控制体内流体上的力；（4）在控制面上存在能量的交换。§2.4.1基本概念\n针对质量m确定的封闭系统τ，上述基本物理定律可以分别表述为：（1）质量方程：表示：系统τ中的质量m不随时间变化。（2）动量方程：表示：系统受外界作用的合外力等于系统的动量对时间的变化率。§2.4.2Lagrange型积分方程\n（3）动量矩方程表示：外界作用于系统上所有外力对某点力矩之和等于系统对同一点的动量矩对时间的变化率。（4）能量方程表示：单位时间内由外界传入系统的热量与外界对系统所做的功之和等于该系统的总能量E对时间的变化率。其中右端括号内为单位质量流体所含内能和动能。§2.4.2Lagrange型积分方程\n上述积分方程称为拉格朗日型积分方程，其特点是：研究对象是质量确定的封闭系统τ，方程中均含有封闭系统中某物理量对时间的变化率。由于流体系统τ的大小和形状均随时间而改变，长时间追踪系统有困难。此外要确切表达系统中物理量随时间的变化率也不容易。有许多流体力学问题往往只关心物体附近确定区域内的速度、作用力等，并不关心具体流体系统的时间历程，拉格朗日型方程对于分析、研究流场来说并不方便，因此实用的是以控制体为研究对象的Euler型积分方程。§2.4.2Lagrange型积分方程\n由质量守恒：这就是积分形式的质量方程。其意义为：控制体中质量的增加率等于净流入控制面的质量流量。xyztτs1s2nEuler型积分方程是对控制体建立的积分方程。利用Reynolds输运方程，可很容易获得。（1）质量方程由雷诺输运方程，取σ＝1，有§2.4.4Euler型积分方程\n由雷诺输运方程，取，有：（2）动量方程由动量守恒原理得：意义为：控制体所受合外力等于控制体中动量的增加率加上净流出控制面的动量流量。－积分形式动量方程§2.4.4Euler型积分方程\n由雷诺输运方程，取，有：（3）动量矩方程由动量矩守恒原理得：－积分形式动量矩方程意义是：控制体所受合外力矩等于控制体中动量矩的增加率加上净流出控制面的动量矩流量。§2.4.4Euler型积分方程\npdsτn由雷诺输运方程，取，有：（4）能量方程由能量守恒原理得：－积分形式能量方程意义是：外界对控制体的传热率和净输入功率等于控制体中能量的增加率加上净流出控制面的能量流量。§2.4.4Euler型积分方程\n我们将系统在初始时刻占据的空间设为控制体，因此在初始瞬间上述对系统输入的加热率和做的功率都可以看成是对控制体的加热率和功率。pdsτn其中，外界对系统做功还可以细分为：流体机械通过轴转动传递的功率称为轴功率（有正负），表面力对系统做功以及彻体力对系统做功。设输入功为正，输出功为负，则水泵、风机等输入正功，涡轮输入负功：§2.4.4Euler型积分方程\n表面力做功还可以分为法向应力做功和切向应力做功。法向应力做功（率）为：切向应力做功（率）为：S为控制体的外表面积上式中的表面剪应力做功（率）一项可以分以下三种情况来考虑：§2.4.4Euler型积分方程\n（1）如果控制面的部分表面为旋转轴表面，则这部分表面上的剪应力做的功率已归入轴功率之中；（2）部分控制面可能为静止固体表面，因为V=0，从而上述剪切应力做功为零；（3）控制面表面是流体进出的通道，此时可以通过适当选择控制面方位和形状使控制面和流体速度相垂直，即剪应力与速度相垂直，从而上述剪切应力做功为零；总之，可以适当选择控制面使剪应力在控制面上做的功（率）为零：§2.4.4Euler型积分方程\n彻体力做功（率）为：τ为控制体的体积设彻体力有势：，有：对于定常流动，第二项由连续方程为零。第一项由高斯公式：§2.4.4Euler型积分方程\n从而：整理得：上式就是常用的积分形式的能量方程。代入：§2.4.4Euler型积分方程\n积分形式质量方程的应用值得指出：质量方程描述流体的质量守恒条件，与流体是否受力无关，与流体属性是否有粘性也无关。积分形式质量方程不描述单独点的细节，它用在控制体上，甚至允许控制体包含流动不连续的地方，例如以后要介绍的激波等处。§2.4.5Euler型积分方程的应用\n例：一段输气管道直径150mm，在相距8m的两个截面上同时量取数据，流入、流出的重量流量分别为2N/s和1.8N/s，问这段管道内气体的平均密度随时间的变化率有多大？解：这是一个非定常问题，流入与流出流量不相等必然造成控制体内质量增加。取这段管道内空间为控制体，由积分形式质量方程：§2.4.5Euler型积分方程的应用\n例：一容积固定为τ的容器装满盐水，初始时刻密度为ρi，纯水（设水密度为ρw）流入容器并与其中盐水充分混合，设流动定常，容器内液位恒定，流入与流出的体积流量不变Q1＝Q2＝Q。求（1）容器内液体混合物的密度变化率；（2）密度变为ρ时（ρi>ρ>ρw）所需的时间。解（1）：划容器内部为控制区。由积分形式质量方程：τ=常数ρwρ§2.4.5Euler型积分方程的应用\n解（2）：由上式：§2.4.5Euler型积分方程的应用\n关于积分形式质量方程的进一步讨论：（1）当密度等于常数时，ρ＝c(必然为不可压)，由上式得：Q1S1S2Q2上述积分可用流入与流出的体积流量Q表为：或说明：当密度等于常数时，流入控制体的体积流量与流出的体积流量相等§2.4.5Euler型积分方程的应用\n（2）当流动为定常可压时，有：设质量流量用表示，得到或说明当流动定常时，流入控制体的质量流量与流出的质量流量相等。注意后一式表示流经控制面任一截面的流量为常数。§2.4.5Euler型积分方程的应用\n说明：在密度不变的一维流动中，流管的粗细将反映流速小大。（3）对于一维流动，控制体如图sV1V2ρ2ρ1A1A2一维流动中，当密度等于常数时，流入的体积流量等于流出的体积流量，可表为§2.4.5Euler型积分方程的应用\n一维流动中，当定常可压时，流入的质量流量等于流出的质量流量，可表为：说明：在定常一维可压流动中，密度ρ、速度V与截面积A的乘积为常数。对式取微分，可以得到定常一维流动质量方程的微分形式：§2.4.5Euler型积分方程的应用\n积分形式动量方程与动量矩方程的应用积分形式动量方程中的合外力指流体受到的所有形式的外力之和，可以包含彻体力、法向表面力和切向表面力，控制体中的物体对于流体的作用力也可以单独考虑。一般来说有两类控制体可供选择：一类是物体不包括在所取控制体之内，而物体的部分壁面构成控制面的一部分，例如管道中的流动；另一类是控制体将流过的物体也包括在内，例如绕机翼的流动。§2.4.5Euler型积分方程的应用\n积分形式的动量方程用于定常、一维管流控制体时（如图），可得：p1、ρ1、V1A1A2xyθ1θ2p2、ρ2、V2对于物体不包括在内的第一类控制体，例如管道，应用积分形式动量方程的目的主要是求管道受到流体的反作用力Rx、Ry。－Rx－Ry方程左端是控制体内流体所受合力在相应坐标系的投影,可包含管璧对流体作用力、重力和两端压力。§2.4.5Euler型积分方程的应用\n设两端的压强分别为p1、p2，管壁对流体的作用力分量为－Rx、－Ry（如上图），不计彻体力，从而动量方程可写为（x方向）：即：如此得到的就是管壁受力。当求管壁所受纯由流动引起的反作用力例如固定管道的螺栓受力时，由于大气压无合力可不考虑，上式中压强用表压。y向同理：§2.4.5Euler型积分方程的应用\n将控制体外部取得离机翼足够远，这样即使翼面附近有粘性力，到了S面上也没有粘性力了，只有压力的作用，从而x方向表面力为：对于如图的第二类控制体（机翼被包含在控制体之内），主要目的是求物体（机翼）受力。我们将动量方程作些变换和说明，得到更常用的形式。设机翼受力在三个方向的分量为Fx、Fy和Fz。则控制体受力的三个分量为－Fx、－Fy和－Fz。(n,x)np§2.4.5Euler型积分方程的应用\n控制体内的x方向彻体力为：从而控制体内x方向所受的合外力为：控制体内x方向的动量随时间变化率及净流出控制面的动量流量为：注：连接S和S1双层面上的面积分为0。§2.4.5Euler型积分方程的应用\n由动量守恒，得：同理：上述方程常常用于定常流动的气体，此时式中的当地变化率一项等于零，且彻体力可以忽略。积分形式动量方程的一个重要方面在于人们不需要知道控制体中的流动细节，只需要知道控制面边界处的流动特性来求作用力，这个作用力可以包含摩擦力的影响在内，例如用上述方程来求物体受到的阻力等。§2.4.5Euler型积分方程的应用\n例．有一种尾迹详测法可以用来测量一个二维物体的型阻（型阻是由粘性直接和间接造成的物体动量法测型阻p1、u1p2、u2解：取控制面S如图。在上游足够远处气体流基本上还没有受到物体的影响还是直匀流。在下游一定距离处气流的静压已经和来流的静压没有什么区别了，但尾迹区速度分布仍然受到影响如图。阻力，例如摩擦阻力和压差阻力）。我们来看一看要测哪些量，并怎样使用积分形式的动量方程。§2.4.5Euler型积分方程的应用\n上下两根流线取在远离物体的地方，那里流速和静压都和原来的来流值一样。在这个S面上作用的静压既然都是同一个值，那末压力做面积分的结果必是零。上下两根流线处没有摩擦力。设定常，不计彻体力，则计算翼型受到的阻力Fx只需计算越过控制面的动量流量：测出尾迹区σ中速度分布即可求出阻力。§2.4.5Euler型积分方程的应用\n例：求宽度为b的二维不可压定常射流对固定斜板（与水平成θ角）的（1）作用力（2）射流宽度比b1/b2（3）力的作用点设不计重力和流动损失。θb,Vb1,V1b2,V2解：由于是自由射流，射流开始处及1、2截面处压强均为大气压。分别沿上下两根流线列不计重力的伯努利方程可得：V1=V2=V（或认为流动均匀无旋，伯努利常数全场成立）由质量方程可知：Q＝Q1＋Q2或b=b1+b2R§2.4.5Euler型积分方程的应用\n（1）求作用力如图建立坐标系，取控制体如图，假设控制体受力为R，由y向动量方程：（注意控制面上大气压无合力）θb,Vb1,V1b2,V2xyR可见θ＝900时受力最大斜板受力与此大小相等方向相反。§2.4.4Euler型积分方程的应用\n（2）求射流宽度比b1/b2由x向动量方程：考虑到：V1=V2=V，有上式与b=b1+b2联立得：故得射流宽度比：这也是流量比Q1/Q2θb,Vb1,V1b2,V2xyR§2.4.5Euler型积分方程的应用\n（3）求力的作用点e设力的作用点距y轴的距离为e，设顺时针方向为矩的正方向，由动量矩方程仅当θ＝900时合力的作用点才通过射流中心θb,Vb1,V1b2,V2xyRe§2.4.5Euler型积分方程的应用\n积分形式的能量方程的应用将积分形式的能量方程应用在进出口处流动参数均匀分布且只有一个进口和一个出口的控制体上，流动定常：1.一维定常流能量方程§2.4.5Euler型积分方程的应用\n注意到质量流量不变，上式除以质量流量化为单位质量形式：该式意义为：对一维控制体加热和做功，等于流出与流入控制面的能量差。写成微分形式，有：§2.4.5Euler型积分方程的应用\n与静止气体的热力学第一定律对比，上式可以称为运动流体在有加热和有输入功时的热力学第一定律，它表明：对流体微团加热和做功，等于微团内能增加、势能增加、动能增加、对外膨胀做功以及压强做功（即流动时压强做功简称流动功）。注意到在重力场下：§2.4.5Euler型积分方程的应用\n2.一维定常流能量方程在各种条件下的表现形式（1）对于理想、定常、不可压、一维、重力场、无机械功输入输出的流动由于加热不会使不可压流体膨胀做功，也不会有摩擦使机械能转化为热能（内能），则内能的变化仅仅是由于外部加热引起的，即dq=du，从而而这就是一维欧拉方程，可积分得伯努利方程：§2.4.5Euler型积分方程的应用\n因此伯努利方程是能量方程在理想、不可压、定常、一维、重力场、无机械功输入输出条件下的特例。（2）在理想、定常、不可压、一维、重力场、有机械功输入输出的条件下，则能量方程化为：§2.4.5Euler型积分方程的应用用这个方程可方便的初步估算风扇对流动做功的功率，利用水库高差发电使涡轮机产生的功率等问题。