2.4--欧拉运动方程及其积分 32页

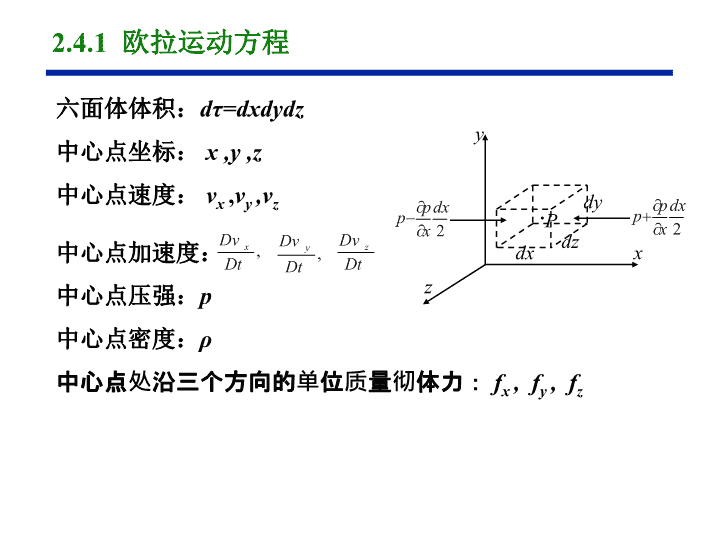
在流场中划出一块三边分别的为dx，dy，dz的微元矩形六面体。不计粘性力，表面力就没有切向力，仅有法向力（压力）一种，而彻体力是可以有的。xyz·Pdxdydz欧拉运动微分方程组是在不计流体粘性前提下推导出来的，该方程实质上是微分形式的动量方程。2.4欧拉运动方程及其积分2.4.1欧拉运动方程\n六面体体积：dτ=dxdydz中心点坐标：x,y,z中心点速度：vx,vy,vz中心点加速度：中心点压强：p中心点密度：ρ中心点处沿三个方向的单位质量彻体力：fx,fy,fzxyz·Pdxdydz2.4.1欧拉运动方程\nx方向的表面力为：x方向的彻体力为：牛顿定律：x方向合外力等于质量乘以x方向加速度，得2.4.1欧拉运动方程\n两边同除以微元体积dxdydz，令其趋于零，并代入加速度的表达，得同理可以写出y和z方向的表达：这就是笛卡尔坐标系下理想流体的欧拉方程。2.4.1欧拉运动方程\n欧拉方程规定了理想流的压强变化与速度变化和彻体力之间的关系。如果在欧拉运动方程中考虑粘性项欧拉方程的向量形式为：2.4.1欧拉运动方程向量形式\n2.4.1欧拉运动方程理想流欧拉方程还可以有另一种表达形式。把加速度的迁移部分改写一下，把迁移加速度部分改写一下：\n式中V是合速，另两个迁移加速度也可以改为类似的式子：得如下形式的理想流欧拉方程称为“格罗米柯－兰姆方程”：\n该形式好处是在方程中显示了旋转角速度，便于分析无旋流动。2.4.1欧拉运动方程\n直匀流对机翼的绕流例.在海平面上，直匀流流过一个机翼，远前方直匀流的静压p＝p∞＝101200牛/米2，流速=100米/秒。已知A，B，C三点的速度分别是VA=0，VB=150米/秒，VC=50米/秒，空气在海平面的ρ=1.255千克/米3。假设流动无旋，求A、B、C三点的压强。2.4欧拉运动方程\n于是：解:流动无旋，伯努利常数全流场通用。由远前方条件得：2.4欧拉运动方程\n2.5环量与涡2.5.1环量与涡的概念研究流动的问题，还有两个极重要的概念:环量和涡。环量的定义：在流场中任取一条封闭曲线，速度沿该封闭曲线的线积分称为该封闭曲线的速度环量。速度环量的符号不仅决定于流场的速度方向，而且与封闭曲线的绕行方向有关，规定积分时逆时针绕行方向为正，即封闭曲线所包围的区域总在行进方向的左侧。\n如果把一个速度向量分成三个坐标轴方向的三个分量vx,vy,vz,把线段ds也分解成dx,dy,dz三个方向：沿曲线AB作速度的线积分沿闭曲线速度的线积分于是环量表达式为：2.5.1环量与涡的概念\n如果流动是无旋的，存在速度势函数Φ，那末上式中的vx,vy,vz都可以用Φ的偏导数表达：说明在无旋流动中，沿着任意一条封闭曲线的速度环量均等于零。但是对有旋流动，上述结论并不成立，绕任意一条封闭曲线的速度环量一般不等于零。2.5.1环量与涡的概念\n旋转轴线都按右手定则确定。涡量概念是指流场中微团角速度之二倍，如平面问题中的2ωz，称为涡量，涡量是个纯运动学的概念。在三维流里，流体微团可以有三个方向的角速度ωx,ωy,ωz,三者合为一个合角速度是：§2.5.1环量与涡的概念\n像流线一样，在同一瞬时，如在流场中有一条曲线，该线上每一点的涡轴线都与曲线相切，这条曲线叫涡线。涡线的微分方程是（给定时刻，t为参量）：涡线给定瞬间，通过某一曲线（本身不是涡线）的所有涡线构成的曲面称为涡面。由封闭涡面组成的管状涡面称为涡管。涡面涡管2.5.2涡线与涡管\n在三维空间问题中，涡通量就是：式中的S是任意形状空间曲面，γ是曲面上微面积dS的法线和ω的轴线之间的夹角。nγ空间问题的涡通量平面问题的涡通量涡线是截面积趋于零的涡管。涡线和涡管的强度都定义为绕涡线或涡管的一条封闭围线的环量。涡量在一个截面上的面积分称为涡通量，在平面问题中，涡通量就是：§2.5.1环量与涡的概念\n在有旋流动中，速度环量与涡量存在着十分密切的联系。为说明这个联系，首先考察二维流场。§2.5.2环量与涡量的关系在二维流场中，任取封闭曲线，然后把该封闭曲线所围成的面积用两组坐标的平行线分割成一系列微小面积，做每一块微小面积的速度环量并求和，得到总的速度环量。对于微元ABCD，速度环量为\n§2.5.2环量与涡量的关系\n绕整个封闭曲线的速度环量为（上图中微元矩形块的重合部分做线积分时因正负号相反而相消）上式即为二维问题中的格林公式。表明：沿平面上一封闭围线L做速度的线积分，所得的环量等于曲线所围面积上每个微团角速度的2倍乘以微团面积之和，即等于通过面积S的涡通量。§2.5.2环量与涡量的关系\n如果围线内没有涡通量，那末沿围线的环量必是零。如果把围线放大一些，尽管面积放大了，但只要包进去的面积里没有涡通量，那么环量值并不会改变。推广到三维空间中的封闭曲线L上，计算的速度环量仍等于二倍角速度乘围线所包的面积，但这面积应取其在与涡线相垂直的平面上的投影值。沿一块有限大的曲面S的围线L的环量仍等于S面上各点的二倍角速度与面积点积：§2.5.2环量与涡量的关系\n展开即：§2.5.2环量与涡量的关系其实这就是是斯托克斯公式，描述曲线积分与曲面积分之间的关系。\n三维流中环量与涡的关系nγ表明：沿空间封闭曲线L的环量，等于穿过张在L上任意曲面S上的涡通量，涡通量的数值与所张的曲面形状无关，只跟围线所包含的涡量有关，无旋时涡通量为零从而沿封闭曲线的速度环量也为零。对于无旋流动还有：说明速度势函数差的意义是沿线段的速度线积分。§2.5.2环量与涡量的关系\n一条强度为Γ的涡线的一段dS对线外的一点P会产生一个诱导速度，情况正像电流会产生磁力的一样。表达涡段所产生的诱导速度的公式是：涡与诱导速度§2.5.2环量与涡量的关系\n这个dV是一个垂直于线段dS与受扰点P所组成的平面的速度（如图），其值正比于涡强Γ和涡段长度dS，但反比于距离r的平方，另外还要乘上r与ds的夹角的θ的正弦。这个公式在形式上和电磁学的电磁感应的比奥—萨瓦公式一样，仍叫比奥—萨瓦公式。或：§2.5.2环量与涡量的关系\n现在把一条强度为Γ的直涡线对线外一点所产生的诱导速度写一下。AB是涡线，P为线外一点，P到AB的距离是h。令任意微段ds与P的连线和AB垂线PN之间夹角为γ，则直线涡的诱导速度ds§2.5.2环量与涡量的关系\nds再令PA与AB的夹角为α；PB与BA的夹角为β。上式积分，γ由到得：这个诱导速度是垂直于纸面的，按图示Γ的方向，它向外指。如果涡线一头是无限长的，那就有：2.5.2环量与涡量的关系\n如果涡线是半无限长，且P点至涡线之垂直足N与涡线的一端重合，则：如果涡线两头都伸展到无限远，则：涡线和环量的概念在空气动力学中十分重要。凡是升力的问题都和涡及环量有关。2.5.2环量与涡量的关系\n’2.5.3理想流中的涡定理描述理想流体中的涡线或涡管有如下定理：定理1沿涡线或涡管涡强不变。见图，在涡管上两条围线PQR和P’Q’R’作两条重合的连线PP’和RR’,沿P’PQRR’Q’P’这样一条围线计算环量，由于所张曲面就是原来涡管的一部分，没有涡线穿过，故总的环量为零：得：这就是说沿涡管任何地方计算它的环量（涡强）其值都是相同的。这条定理称为海姆霍兹第一定理，或简称第一涡定理。由于环量等于涡通量，因此沿同一涡管，涡管细处转速必然快反之涡管粗处转速必然慢。\n涡管强度守恒（左图）和涡管可能存在的形式（右图）定理2：一根涡管在流体里不可能中断，可以伸展到无限远去，可以自相连接成一个涡环（不一定是圆环），也可以止于边界，固体的边界或自由边界（如自由液面）。这条定理可以用第一定理的结论推演而得到证明。第一定理说，涡强沿涡管不变。如果涡管到某处突然中止了，那末涡强也就应该随之变为零，而这是违反第一定理的，所以是不可能的。§2.5.3理想流中的涡定理此定理称为海姆霍兹第二定理，或简称第二涡定理。\n§2.5.3理想流中的涡定理定理3开尔文kelvin定律(环量不变定律)：在理想流中，涡的强度不随时间变化，既不会增强，也不会削弱或消失。实际飞机的尾涡\n实际流体都是有粘性的，涡强是会随时间变化的。不过空气的粘性很小，机翼上的涡随着气流流下去，离机翼很远之后它对机翼的作用就趋于零了，而在离机翼不太远的范围内，粘性使涡强的衰减并不很显著，所以计算涡对机翼的作用时，可以不必考虑粘性的衰减作用，当作它在理想流中强度不衰减去处理就行了。§2.5.3理想流中的涡定理陆龙卷\n本章基本要求了解两种描述流场的方法的区别与特点，重点掌握欧拉法下加速度的表达和意义掌握流体微团的几种变形和运动及其数学表达，掌握流体微团的运动分解与刚体运动的异同；了解系统分析方法与控制体分析方法的区别与联系，掌握雷诺输运方程的表达及意义；空气动力学基本方程是本章重点:微分形式方程要重点掌握连续方程、欧拉方程和能量方程的表达和意义；掌握微元控制体分析方法；掌握伯努利方程的表达、意义、条件和应用；重点需要掌握的概念：流线、流量、散度、旋度、速度势函数、流函数、环量与涡的表达、意义及其相互之间的关系.