2018学年高中物理 精做09 带电粒子在组合场中的运动大题精做 新人教版-选修1 14页

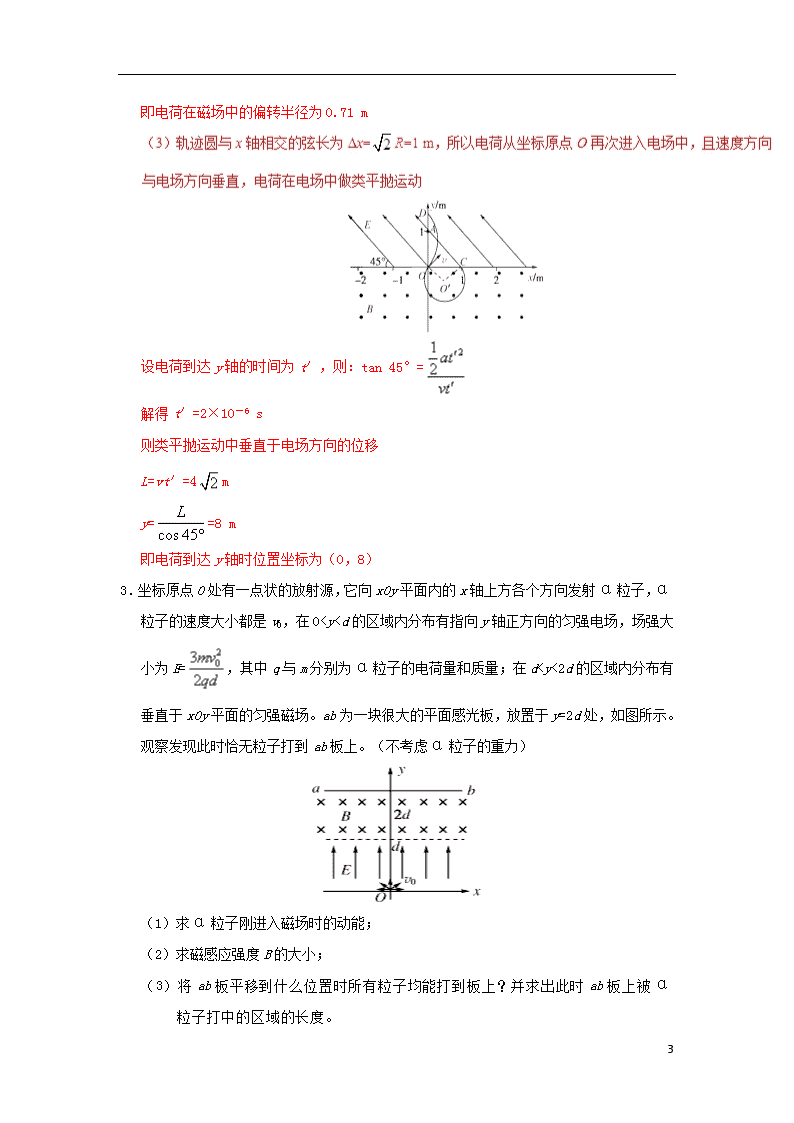
-精做09带电粒子在组合场中的运动1．如图所示，两平行金属板间距为d，电势差为U，板间电场可视为匀强电场；金属板上方有一磁感应强度为B的匀强磁场。电荷量为+q、质量为m的粒子，由静止开始从正极板出发，经电场加速后射出，从M点进入磁场后做匀速圆周运动，从N点离开磁场。忽略重力的影响。（1）求匀强电场场强E的大小；（2）求粒子从电场射出时速度ν的大小；（3）求M、N两点间距L的大小；保持粒子不变，请你说出一种增大间距L的方法。【答案】（1）（2）（3）只增大U或只减小B等（3）根据牛顿第二定律可得：②L=2R③联立①②③式可得增大间距L的方法有：只增大U或只减小B等2．在如图所示的直角坐标系中，x轴的上方存在与x轴正方向成45°14\n-角斜向右下方的匀强电场，场强的大小为E=×104V/m。x轴的下方有垂直于xOy面向外的匀强磁场，磁感应强度的大小为B=2×10－2T。把一个比荷为=2×108C/kg的正电荷从坐标为（0，1）的A点处由静止释放。电荷所受的重力忽略不计。（1）求电荷从释放到第一次进入磁场时所用的时间；（2）求电荷在磁场中做圆周运动的半径；（保留两位有效数字）（3）当电荷第二次到达x轴时，电场立即反向，而场强大小不变，试确定电荷到达y轴时的位置坐标。【答案】（1）10－6s（2）0.71m（3）（0，8）加速度a==2×1012m/s2时间t==10－6s（2）电荷到达C点的速度为v=at=2×106m/s速度方向与x轴正方向成45°角，在磁场中运动时由得R==m14\n-即电荷在磁场中的偏转半径为0.71m设电荷到达y轴的时间为t′，则：tan45°=解得t′=2×10－6s则类平抛运动中垂直于电场方向的位移L=vt′=4my==8m即电荷到达y轴时位置坐标为（0，8）3．坐标原点O处有一点状的放射源，它向xOy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小都是v0，在01）。一质量为m、电荷量为q（q>0）的带电粒子以速度v0从坐标原点O沿x轴正向射入磁场，此时开始计时，当粒子的速度方向再次沿x轴正向时，求（不计重力）14\n-（1）粒子运动的时间；（2）粒子与O点间的距离。【答案】（1）（2）②粒子速度方向转过180°时，所用时间t1为③粒子再转过180°时，所用时间t2为④联立①②③④式得，所求时间为⑤（2）由几何关系及①②式得，所求距离为⑥【名师点睛】对于带电粒子在磁场中运动问题，解题时常要分析带电粒子受到的洛伦兹力的情况，找到粒子做圆周运动的圆心及半径，画出运动轨迹可以使运动过程清晰明了，同时要善于运用几何知识帮助分析和求解。8．（2017·江苏卷）一台质谱仪的工作原理如图所示。大量的甲、乙两种离子飘入电压为U0的加速电场，其初速度几乎为0，经过加速后，通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片上。已知甲、乙两种离子的电荷量均为+q，质量分别为2m和m，图中虚线为经过狭缝左、右边界M、N14\n-的甲种离子的运动轨迹。不考虑离子间的相互作用。（1）求甲种离子打在底片上的位置到N点的最小距离x；（2）在答题卡的图中用斜线标出磁场中甲种离子经过的区域，并求该区域最窄处的宽度d；（3）若考虑加速电压有波动，在（）到（）之间变化，要使甲、乙两种离子在底片上没有重叠，求狭缝宽度L满足的条件。【答案】（1）（2）（3）【解析】（1）设甲种离子在磁场中的运动半径为r1电场加速且解得根据几何关系x=2r1–L解得14\n-（3）设乙种离子在磁场中的运动半径为r2r1的最小半径r2的最大半径由题意知2r1min–2r2max>L，即解得【名师点睛】本题考查带电粒子在匀强磁场中的运动，对此类问题主要是画出粒子运动的轨迹，分析粒子可能的运动情况，找出几何关系，有一定的难度。9．（2016·江苏卷）回旋加速器的工作原理如图1所示，置于真空中的D形金属盒半径为R，两盒间狭缝的间距为d，磁感应强度为B的匀强磁场与盒面垂直，被加速粒子的质量为m，电荷量为+q，加在狭缝间的交变电压如图2所示，电压值的大小为U0。周期T=。一束该种粒子在t=0~时间内从A处均匀地飘入狭缝，其初速度视为零。现考虑粒子在狭缝中的运动时间，假设能够出射的粒子每次经过狭缝均做加速运动，不考虑粒子间的相互作用。求：（1）出射粒子的动能；（2）粒子从飘入狭缝至动能达到所需的总时间；（3）要使飘入狭缝的粒子中有超过99%能射出，d应满足的条件。14\n-图1图2【答案】（1）（2）（3）【答案】（1）粒子运动半径为R时且解得由，解得（3）只有在0~时间内飘入的粒子才能每次均被加速则所占的比例为由，解得【方法技巧】考查回旋加速器的原理，能获得的最大速度对应最大的轨道半径，即D形盒的半径，粒子在加速器运动的时间分两部分，一是在磁场中圆周运动的时间，二是在电场中的匀加速运动时间，把加速过程连在一起就是一匀加速直线运动。14