2017春上海教育版数学七下15.2《直角坐标平面内点的运动》word导学案 7页

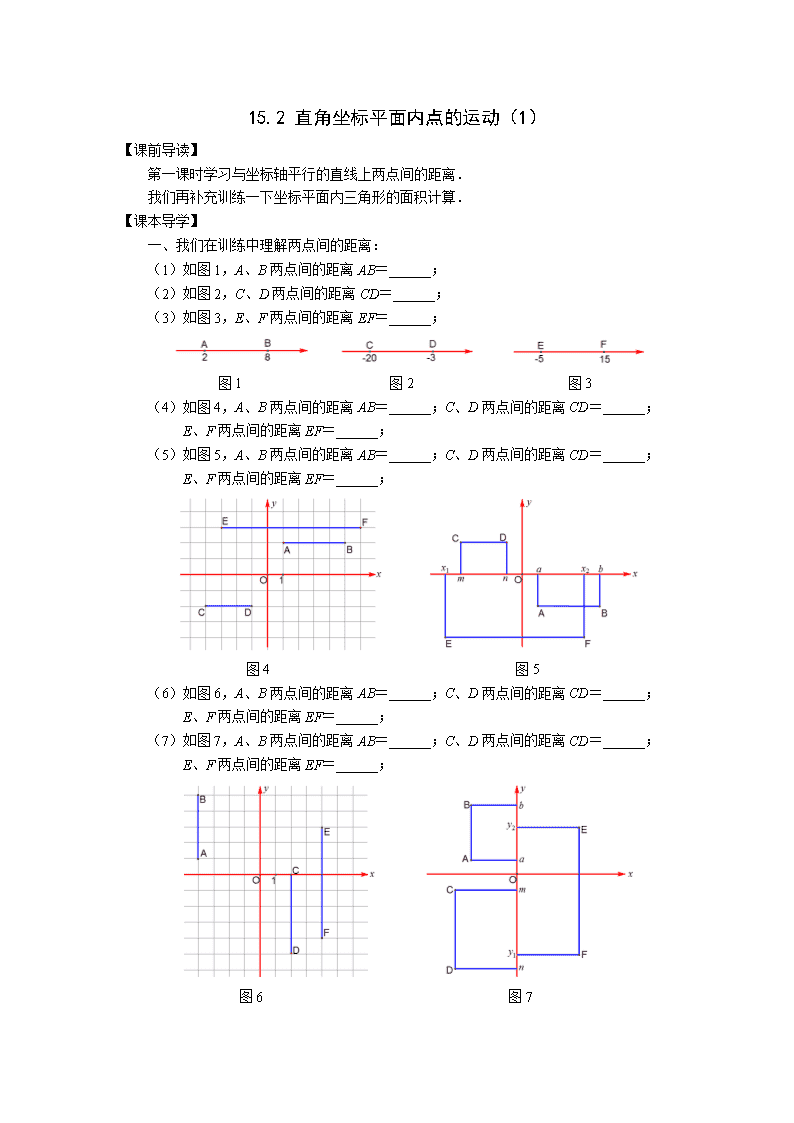
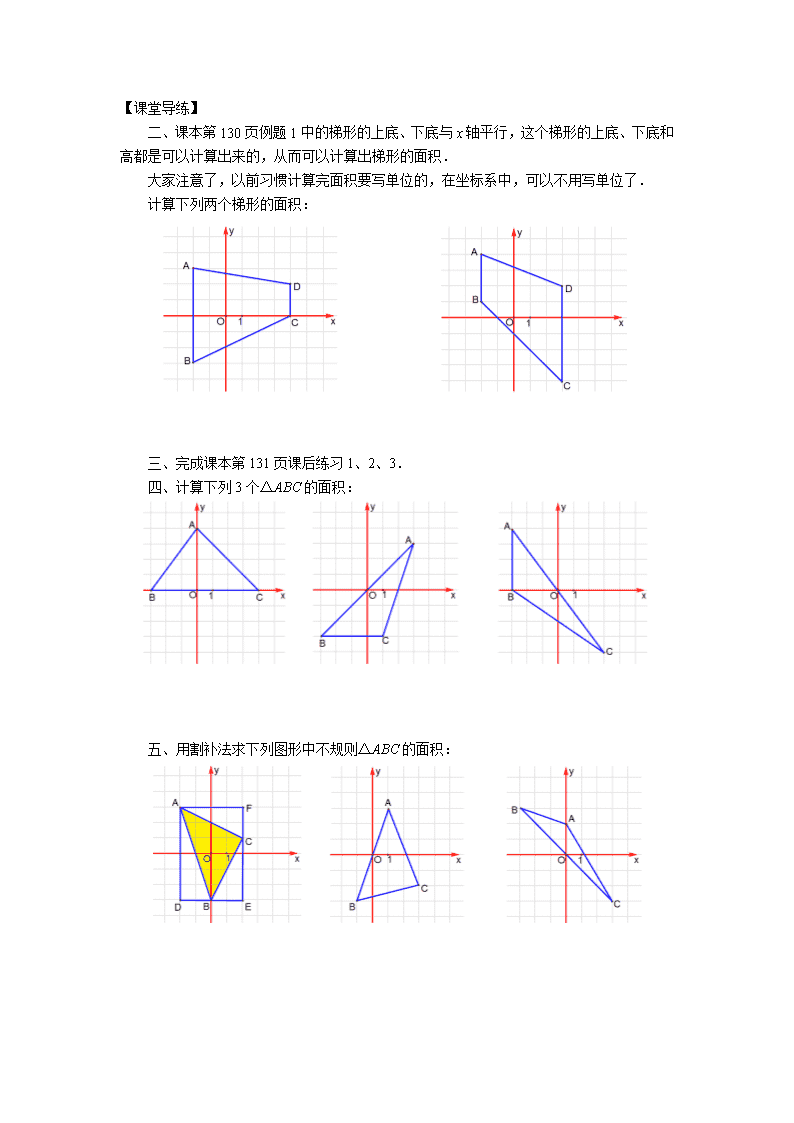
15.2直角坐标平面内点的运动（1）【课前导读】第一课时学习与坐标轴平行的直线上两点间的距离．我们再补充训练一下坐标平面内三角形的面积计算．【课本导学】一、我们在训练中理解两点间的距离：（1）如图1，A、B两点间的距离AB＝______；（2）如图2，C、D两点间的距离CD＝______；（3）如图3，E、F两点间的距离EF＝______；图1图2图3（4）如图4，A、B两点间的距离AB＝______；C、D两点间的距离CD＝______；E、F两点间的距离EF＝______；（5）如图5，A、B两点间的距离AB＝______；C、D两点间的距离CD＝______；E、F两点间的距离EF＝______；图4图5（6）如图6，A、B两点间的距离AB＝______；C、D两点间的距离CD＝______；E、F两点间的距离EF＝______；（7）如图7，A、B两点间的距离AB＝______；C、D两点间的距离CD＝______；E、F两点间的距离EF＝______；图6图7\n【课堂导练】二、课本第130页例题1中的梯形的上底、下底与x轴平行，这个梯形的上底、下底和高都是可以计算出来的，从而可以计算出梯形的面积．大家注意了，以前习惯计算完面积要写单位的，在坐标系中，可以不用写单位了．计算下列两个梯形的面积：三、完成课本第131页课后练习1、2、3．四、计算下列3个△ABC的面积：五、用割补法求下列图形中不规则△ABC的面积：\n15.2直角坐标平面内点的运动（2）【课前导读】第二课时学习点在坐标平面内的平移与坐标的关系．包括一次平移（向左、向右、向上或向下）和两次平移（先左右方向，再上下方向或先上下方向，再左右方向）．【课本导学】一、我们在训练中理解点的平移与坐标的关系：（1）如图1，点A(___,___)向右平移5个单位后得到点A′(___,___)，点B(___,___)向左平移5个单位后得到点B′(___,___)，点C(___,___)向右平移4个单位后得到点C′(___,___)，点D(___,___)向左平移3个单位后得到点D′(___,___)；（2）如图2，点A(___,___)向下平移5个单位后得到点A′(___,___)，点B(___,___)向上平移5个单位后得到点B′(___,___)，点C(___,___)向下平移3个单位后得到点C′(___,___)，点D(___,___)向上平移4个单位后得到点(___,___)；图1图2（3）点在坐标平面内左、右平移_____坐标不变；（4）点在坐标平面内上、下平移_____坐标不变．【课堂导练】二、完成下列填空：（1）如图1，点A(－2,1)向右平移20个单位后得到点A′(___,___)，点B(－20,0)向左平移10个单位后得到点B′(___,___)，点C(0,－12)向右平移14个单位后得到点C′(___,___)，点D(18,－2)向左平移30个单位后得到点D′(___,___)；（2）如图2，点A(－2,1)向下平移20个单位后得到点A′(___,___)，点B(－20,0)向上平移10个单位后得到点B′(___,___)，点C(0,－12)向下平移14个单位后得到点C′(___,___)，点D(18,－2)向上平移30个单位后得到点(___,___)；（3）点A(m,n)向右平移5个单位后得到点A′(_____,_____)，点B(x,y)向左平移a个单位后得到点B′(_____,_____)；（4）点A(m,n)向下平移5个单位后得到点A′(_____,_____)，\n点B(x,y)向上平移a个单位后得到点B′(_____,_____)．三、完成课本第133页课后练习1、2．四、课本第133页课后练习3的图形太小，不便于同学们探究、练习，请在下面放大了的图形中完成．题目：将直角坐标平面内的已知图形先向上平移5个单位，接着向左平移4个单位，画出经过这两次平移后得到的图形；再写出点A、B、C、D、E、G所对应的点的坐标．A(_______)，B(_______)，C(_______)，D(_______)，E(_______)，G(_______)；A′(_______)，B′(_______)，C′(_______)，D′(_______)，E′(_______)，G′(_______)；A′′(_______)，B′′(_______)，C′′(_______)，D′′(_______)，E′′(_______)，G′′(_______)．\n15.2直角坐标平面内点的运动（3）【课前导读】第三课时学习3个内容：1．关于x轴对称的两个点的坐标由什么关系？2．关于y轴对称的两个点的坐标由什么关系？3．关于原点O对称的两个点的坐标由什么关系？【课本导学】一、我们在训练中理解两个对称的点的坐标关系：（1）如图1，点A(______)与点B(______)、点C(______)与点D(______)、点E(______)与点F(______)关于____轴对称，两个对称点的____坐标相等，____坐标互为相反数；（2）如图2，点A(______)与点B(______)、点C(______)与点D(______)、点E(______)与点F(______)关于____轴对称，两个对称点的____坐标相等，____坐标互为相反数；（3）如图3，点A(______)与点A′(______)、点B(______)与点B′(______)、点C(______)与点C′(______)、点D(______)与点D′(______)关于_____对称，两个对称点的横坐标_____________，纵坐标_____________．【课堂导练】\n二、完成课本第136页课后练习1、3、5．三、课本第136页课后练习2、4的图形太小，不便于同学们探究、练习，请在下面放大了的图形中完成．课后练习2题目如下左图，画出△ABC分别关于x轴、y轴对称的图形△A1B1C1和△A2B2C2，再写出各个三角形的顶点坐标．课后练习2题目如下右图，画出四边形OABC关于原点O对称的四边形OA1B1C1，再写出这两个四边形的顶点坐标．A(_______)，B(_______)，C(_______)；A(_______)，B(_______)，C(_______)；A1(_______)，B1(_______)，C1(_______)；A1(_______)，B1(_______)，C1(_______)．A2(_______)，B2(_______)，C2(_______)．四、我们补充训练一下画图形绕着原点旋转90°．（1）在图1中，把长方形OBAC绕着点O逆时针旋转90°．（2）在图1中，把长方形OBAC绕着点O顺时针旋转90°．（3）在图2中，把△OAB绕着点O逆时针旋转90°．（4）在图3中，把△OAB绕着点O顺时针旋转90°．图1图2\n