陕西省西安市八校2020届高三上学期期末考试数学（文）试卷 9页

陕西省西安市八校 2020 届高三上学期 期末考试数学（文）试卷 第Ⅰ卷(选择题共 60 分) 一、选择题：（本大题共 12 小题，每小题 5 分，共 60 分.） 1．已知集合 { N | 4}A x x   ， { | 3 3}B x x    ，则 A B  （） A．{1,2}B．{0,1,2}C．{ 3, 4} D．{ 3,3} 2．设复数满足  2 5z i  ，则在复平面内 z对应的点在（） A．第四象限 B．第三象限 C．第二象限 D．第一象限 3．命题“任意 0x  ， 1 1x x   ”的否定是( ) A．存在 0 0x  ， 0 0 1 1x x   B．存在 0 0x  ， 0 0 1 1x x   C．任意 0x  ， 1 1x x   D．任意 0x  ， 1 1x x   4．总体由编号为 01，02，…，19，20 的 20 个个体组成．利用下面的随机数表选取 5 个个 体，选取方法从随机数表第 1 行的第 5 列和第 6 列数字开始由左到右一次选取两个数字，则 选出来的第 5 个个体的编号为（） 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4935 8200 3623 4869 6938 7481 A．08 B．07 C．02 D．01 5．若直线 2 2 0( 0, 0)ax by a b     ，被圆 2 2 2 4 1 0x y x y     截得弦长为 4，则 4 1 a b  的最小值是（ ）． A．9 B．4 C． 1 2 D． 1 4 6．若函数 , 1( ) (3 ) 1, 1 xa xf x a x x       满足： 1 2,x x R  ，且 1 2x x 都有 1 2 1 2( )[ ( ) ( )] 0x x f x f x   ，则实数的取值范围是（ ） A．(1,2] B．[2, 3) C． (2,3) D．(1,3) 7．一个圆柱的底面直径与高都等于一个球的直径，则圆柱的全面积与球的表面积之比为 （ ） A． 2 :1 B． 4:3 C．3:2 D．1:1 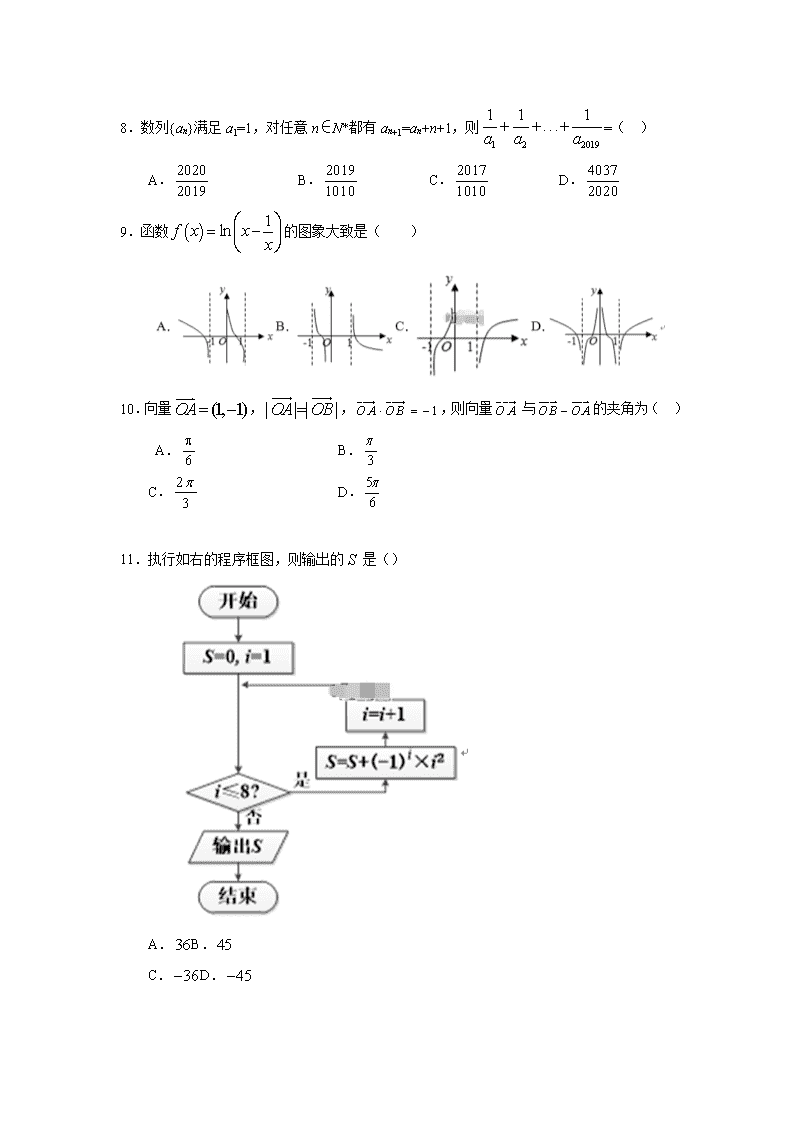8．数列{an}满足 a1=1，对任意 n∈N*都有 an+1=an+n+1，则 1 2 2019 1 1 1 a a a   =（ ） A． 2020 2019 B． 2019 1010 C． 2017 1010 D． 4037 2020 9．函数   1lnf x x x      的图象大致是（ ） 10．向量 (1, 1)OA  ，| | | |OA OB  ， 1OA OB    ，则向量 O A  与OB OA  的夹角为（ ） A． 6  B． 3  C． 2 3  D． 5 6  11．执行如右的程序框图，则输出的 S 是（） A．36B． 45 C． 36 D． 45 12．已知函数 ( )( )f x x R 满足 (1) 1f  ，且 ( ) 1f x  ，则不等式  2 2lg lgf x x 的解集 为（ ） A． 10,10      B． C． 1 ,1010      D． 10, 第Ⅱ卷(非选择题共 90 分) 二、填空题：（本大题共 4 小题，每小题 5 分，共 20 分。请将正确答案填写在答题纸相应 位置.） 13．若 na 是等比数列，且公比 4q  ， 1 2 3 21a a a   ，则 na  ________. 14．已知实数、满足条件则的最大值为________. 15．已知在 ABC 中，角 A ， B ，C 的对边分别为，b，c， π 3A  ， 2b  ， ABC 的 面积等于 2 3，则 ABC 外接圆的面积为________. 16．双曲线 C： 2 2 2 2 x y a b  1（a＞0，b＞0）的左右焦点为 F1，F2（|F1F2|＝2c），以坐标原点 O 为圆心，以 c 为半径作圆 A，圆 A 与双曲线 C 的一个交点为 P，若三角形 F1PF2 的面积为 a2，则 C 的离心率为________. 三、解答题：(共 70 分.解答应写出文字说明、证明过程或演算步骤.) （一）必考题：共 60 分. 17．（12 分）已知函数 1( ) (sin sin ),2f x x x x R   （1）求函数 ( )f x 的最小正周期 T 和单调递增区间； （2）若  0,x  ，且关于 x 的函数 2( ) 2 ( ) 2 ( ) 2 1g x f x f x a    的最小值为 1 2 ，求 的值. 18．（12 分）某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取 了部分学生的分数（得分取正整数，满分为 100）作为样本（样本容量为n）进行统计，按 照 50,60 ， 60,70 ， 70,80 ， 80,90 ， 90,100 的分组作出频率分布直方图，已 知得分在 50,60 ， 90,100 的频数分别为 8，2． （1）求样本容量n和频率分布直方图中的 x，y 的值； （2）估计本次竞赛学生成绩的中位数； （3）在选取的样本中，从竞赛成绩在 80 分以上（含 80 分）的学生中随机抽取 2 名学生， 求所抽取的 2 名学生中至少有一人得分在 90,100 内的概率． 19．（12 分）在如图所示的多面体中，四边形 ABCD 是平行四边形,四边形 BDEF 是矩形. (1)求证： / /AE 平面 BFC ； (2)若 AD DE ， 1AD DE  ， 2AB ， 60BAD   ，求三棱锥 F AEC 的体积. 20．（12 分）设 O 为坐标原点，椭圆 2 2 2 2: 1( 0)x yC a ba b     的焦距为 4 5 ，离心率为 2 5 5 ， 直线 : ( 0)l y kx m m   与 C 交于 A ， B 两点． （1）求椭圆 C 的方程； （2）设点 (0,1) 4P PA PB  ， ，求证：直线 l 过定点，并求出定点的坐标． 21．（12 分）已知函数 21( ) ln 1( )2f x x a x a R    . （1）讨论函数 ( )f x 的单调性； （2）若 2 0a  ＜ ，对任意  1 2, 1,2x x  ，不等式 1 2 1 2 1 1( ) ( )f x f x m x x    恒成立，求 实数 m的取值范围. （二）选考题：共 10 分.请考生在第 22，23 题中任选一题作答.如果多做，那么按所做的第 一题计分. 22.（10 分）【选修 4-4：坐标系与参数方程】 在平面直角坐标系 xOy 中，曲线 C 的参数方程为 3cos 3sin x y     （ 为参数），在以原点 为极点， x轴正半轴为极轴的极坐标系中，直线 l 的极坐标方程为 2sin 4 2       ． （1）求曲线 C 的普通方程和直线 l 的直角坐标方程； （2）设点  1,0P  ，直线 l 和曲线 C 交于 ,A B 两点，求| | | |PA PB 的值． 23.（10 分）【选修 4-5：不等式选讲】 已知函数    3 1 3 , 4f x x x k g x x      ． （1）当 3k   时，求不等式   4f x  的解集； （2）设 1k   ，且当 1[ , )3 3 kx   时，都有    f x g x ，求k的取值范围． 一. 选择题（本大题包括 12 小题，每小题 5 分，共 60 分.） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B D B D A B C B C D A B 二.填空题（本大题包括 4 小题，每小题 5 分，共 20 分.） 13. 14 n 14. 1 15. 4 16. 2 三.解答题（本大题包括 6 小题，共 70 分.） 17. 解：解：（1） 1( ) (sin | sin |)2f x x x  sin ,sin 0 sin , 2 2 ,0,sin 0 0, 2 2 2 x x x k x k k Zx k x k                    则函数  f x 的周期 T 2 ; 函数  f x 的增区间 2 , 2 ( )2k k k Z      ………6 分 （ 2 ） 2( ) 2 sin 2 sin (2 1)g x x x a    , 令 sinx t 可 得  0,1t  换 元 可 得 22 2 (2 1)y t t a    ，对称轴为 1 2t  3 1(2 ) , 1.2 2a a       ……………12 分 18．解：（1）由题意可知，样本容量 n= 8 0.016 10 =50， ，x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030； ………………4 分 （2）设本次竞赛学生成绩的中位数为 m，平均分为 x ， 则[0.016+0.03]×10+（m﹣70）×0.040 =0.5，解得 71m  ， ………………8 分 （3）由题意可知，分数在[80，90）内的学生有 5 人，记这 5 人分别为 a1，a2，a3，a4，a5， 分数在[90，100]内的学生有 2 人，记这 2 人分别为 b1，b2．抽取的 2 名学生的所有情况有 21 种，分别为:（a1，a2）,（a1，a3），（a1，a4）,（a1，a5）,（a1，b1）,（a1，b2），（a2，a3）, （a2，a4）,（a2，a5）,（a2，b1），（a2，b2）,（a3，a4）,（a3，a5）,（a3，b1）,（a3，b2）, （a4，a5）,（a4，b1）,（a4，b2）,（a5，b1）,（a5，b2）,（b1，b2）． 其中 2 名同学的分数都不在[90，100]内的情况有 10 种，分别为:（a1，a2）,（a1，a3）,（a1， 数学(文科)试题答案 a4）,（a1，a5）,（a2，a3）,（a2，a4）,（a2，a5）,（a3，a4）,（a3，a5）,（a4，a5）． ∴所抽取的 2 名学生中至少有一人得分在[90，100]内的概率 10 111 21 21p    . …………12 分 19. 解：（1） 四边形 ABCD 为平行四边形 / /AD BC 又 AD平面 BCF ， BC 平面 BCF / /AD 平面 BCF  四边形 BDEF 为矩形 / /DE BF 又 DE 平面 BCF ， BF 平面 BCF / /DE 平面 BCF ,AD DE  平面 ADE ， AD DE D   平面 / /ADE 平面 BCF 又 AE平面 ADE / /AE 平面 BFC ……………6 分 （2）设 AC BD O ，连接 ,OE OF  四边形 ABCD 为平行四边形 O 为 AC 中点 2 2F A E C C A E F O A E F A O E FV V V V       在 ABD 中，由余弦定理得： 2 2 2 2 cos 4 1 2 3BD AB AD AD AB BAD         3B D  2 2 2AB AD BD  AD BD  又 AD DE ， ,BD DE  平面 BDEF ， BD DE D  AD 平面 BDEF  点 A 到平面 OEF 的距离为 AD 1 1 3 2 2 2OEF BDEFS S BD DE     ， 1AD 1 2 3 32 2 13 3 2 3F AEC A OEF OEFV V S AD           ……………………12 分 20. 解：（1） 2 4 5 2 5c c   因为 2 5 5 ce a   ，则 5a  故 5b ，所以椭圆 C 的方程为 2 2 125 5 x y  ………………………4 分 （ 2 ） 设  1 1,A x y ，  2 2,B x y ， 联 立 2 2 125 5 y kx m x y     ， 消 去 y 整 理 可 得  2 2 21 5 10 5 25 0k x mkx m     所以   ， 1 2 2 10 1 5 kmx x k     ， 2 1 2 2 5 25 1 5 mx x k   所以  1 2 1 2 2 22 1 5 my y k x x m k           2 2 1 2 1 2 1 2 1 2y y kx m kx m k x x km x x m       2 2 2 2 2 2 2 2 2 2 2 2 5 25 10 5 25 1 5 1 5 k m k k m m k m k m k k         因为 (0,1)P ， 4PA PB    所以     1 1 2 2 1 2 1 2 1 2, 1 , 1 1 4x y x y x x y y y y          所以 2 2 2 2 2 2 5 25 25 2 5 01 5 1 5 1 5 m k m m k k k         整理可得 23 10 0m m   解得 2m 或 5 3m   （舍去）所以直线 l 过定点 (0, 2) ………12 分 21.解：（1）∵依题意可知：函数 ( )f x 的定义域为 0,  ，∴ 2 ( ) a x af x x x x     ， 当 0a 时， ( ) 0f x  在 0,  恒成立，所以 ( )f x 在 0,  上单调递增. 当 0a  时，由 ( ) 0f x  得 x a ；由 ( ) 0f x  得 0 x a  ； 综上可得当 0a 时， ( )f x 在 0,  上单调递增； 当 0a  时， ( )f x 在 0, a 上单调递减；在 ,a  上单调递增.………………6 分 （2）因为 2 0a   ，由（1）知，函数 ( )f x 在 1, 2 上单调递增， 不妨设 1 21 2x x   ，则 1 2 1 2 1 1( ) ( )f x f x m x x    ，可化为 2 1 2 1 ( ) ( )m mf x f xx x    ， 设 21( ) ( ) ln 12 m mh x f x x a xx x       ，则 1 2( ) ( )h x h x ，所以 ( )h x 为  1, 2 上的减函 数， 即 2( ) 0a mh x x x x     在 1, 2 上恒成立，等价于 3m x ax  在 1, 2 上恒成立， 设 3( )g x x ax  ，所以 m ax( )m g x ， 因 2 0a  ＜ ，所以 2( ) 3 0＞  g x x a ，所以函数 ( )g x 在 1, 2 上是增函数， 所以 m ax( ) (2) 8 2 12g x g a    （当且仅当 2a   时等号成立）所以 12m ．………12 分 22.解:（1）因为曲线 C 的参数方程为 3cos 3sin x y     （ 为参数）， 所以曲线 C 的普通方程为 2 2 19 3 x y  .因为 2sin 4 2       ， 所以 sin cos 1, 1 0x y         .所以直线 l 的直角坐标方程为 1 0x y   .…5 分 （2）由题得点  1,0P  在直线 l 上，直线 l 的参数方程为 21 2 2 2 x t y t       ， 代入椭圆的方程得 22 2 8 0t t   ，所以 1 2 1 2 2+ , 4 02t t t t    ， 所以 2 1 2 1 2 1 2 66|PA|+|PB|=| | ( ) 4 2t t t t t t     .…………………10 分 23.解：（1）当 3k   时，   16 4, 3 12 13 6 4, 1 x x f x x x x            ， 故不等式   4f x  可化为： 1 6 4 4 x x     或 1 13 2 4 x     或 1 3 6 4 4 x x      ， 解得： 0x  或 4 3x  ， 所求解集为{ | 0x x  或 4}3x  ．…………5 分 （2）（2）当 1,3 3 kx      时，由 1k   有： 3 1 0,3 0x x k       1f x k  。 不等式    f x g x 可变形为：1 4k x   故 3k x  对 1,3 3 kx      恒成立，即 33 kk    ，解得 9 4k  而 1k   ，故 91 4k   ． k的取值范围是 91, 4    .……………………10 分