四川省自贡市富顺县第二中学2019-2020学年高一上学期期中考试数学试卷 10页

www.ks5u.com 高中数学试卷 一．选择题（共12小题）‎ ‎1．若集合A＝{x|﹣1＜x＜2}，B＝{﹣2，0，1，2}，则A∩B＝（　　）‎ A．∅ B．{0，1} C．{0，1，2} D．{﹣2，0，1，2}‎ ‎【解答】解：A＝{x|﹣1＜x＜2}，B＝{﹣2，0，1，2}，∴A∩B＝{0，1}．故选：B．‎ ‎【点评】考查描述法、列举法的定义，以及交集的运算．‎ 2． 幂函数的图像经过，则解析式为（ ）‎ A． ‎ B． C． D．‎ 答案：B ‎3．已知函数，则的值是（　　）‎ A．﹣1 B．3 C． D．‎ ‎【解答】解：由题意可得，f（）＝＝﹣1‎ ‎∴f（f（））＝f（﹣1）＝3﹣1＝故选：C．‎ ‎【点评】本题主要考 查了分段函数的函数值的求解，解题的关键是根据不同的自变量的值确定函数的解析式，属于基础试题 ‎4．函数y＝3x（x≤0）的值域是（　　）‎ A．（0，1） B．（﹣∞，1） C．（0，1] D．[0，1）‎ ‎【解答】解：∵y＝3x（x≤0）为增函数，且3x＞0，‎ ‎∴30＝1，∴0＜y≤1．∴函数的值域为（0，1]．故选：C．‎ ‎【点评】本题考查的是函数值域的求法，关键是要熟悉指数函数的单调性，本题计算量极小，属于容易题．‎ ‎5、设a＝lg2，b＝lg3，则log26＝（　　）‎ A．ab2 B．a2b C． D．‎ ‎【解答】解：∵a＝lg2，b＝lg3，‎ ‎∴．故选：C．‎ ‎【点评】考查对数的换底公式，以及对数的运算性质．‎ ‎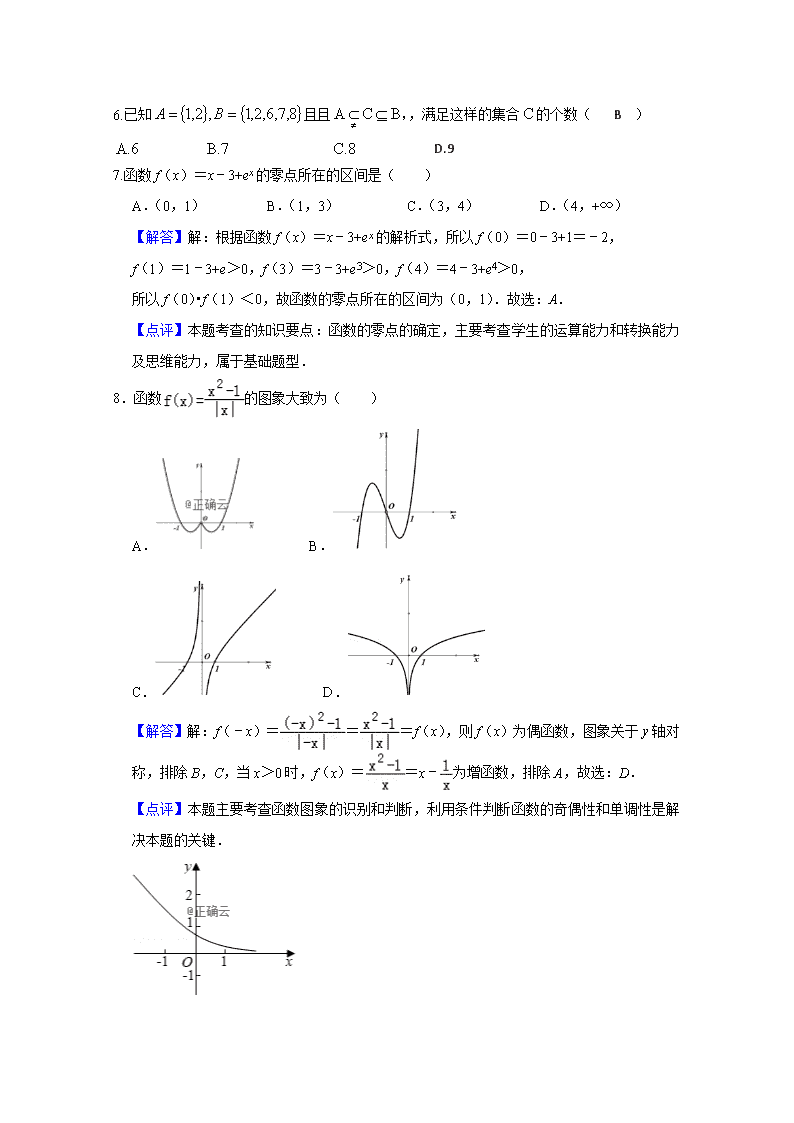6.已知且且，满足这样的集合的个数（ B ）‎ ‎ D.9‎ ‎7.函数f（x）＝x﹣3+ex的零点所在的区间是（　　）‎ A．（0，1） B．（1，3） C．（3，4） D．（4，+∞）‎ ‎【解答】解：根据函数f（x）＝x﹣3+ex的解析式，所以f（0）＝0﹣3+1＝﹣2，‎ f（1）＝1﹣3+e＞0，f（3）＝3﹣3+e3＞0，f（4）＝4﹣3+e4＞0，‎ 所以f（0）•f（1）＜0，故函数的零点所在的区间为（0，1）．故选：A．‎ ‎【点评】本题考查的知识要点：函数的零点的确定，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．‎ ‎8．函数的图象大致为（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：f（﹣x）＝＝＝f（x），则f（x）为偶函数，图象关于y轴对称，排除B，C，当x＞0时，f（x）＝＝x﹣为增函数，排除A，故选：D．‎ ‎【点评】本题主要考查函数图象的识别和判断，利用条件判断函数的奇偶性和单调性是解决本题的关键．‎ ‎9．函数f（x）＝ax﹣b的图象如图所示，其中a，b为常数，则loga（1﹣b）的取值为（　　）‎ A．等于0 B．恒小于0 C．恒大于0 D．无法判断 ‎【解答】解：由图象可知，0＜a＜1，令x＝0，可得图象与y轴的交点为（0，a﹣b），‎ 显然a﹣b＜1，即a﹣b＜a0．∴b＜0．则1﹣b＞1．那么loga（1﹣b）＜0．故选：B．‎ ‎【点评】本题考查的知识点是对数函数，指数函数的图象性质的应用，熟练掌握各种基本初等函数的图象和性质．‎ ‎10．已知函数f（x）＝loga（x+2）+3的图象恒过定点（m，n），且函数g（x）＝mx2﹣2bx+n在[1，+∞）上单调递减，则实数b的取值范围是（　　）‎ A．[1，+∞） B．[﹣1，+∞） C．（﹣∞，﹣1） D．（﹣∞，1）‎ ‎【解答】解：∵函数f（x）＝loga（x+2）+3的图象恒过定点（m，n），令x+2＝1，求得x＝﹣1、y＝3，可得它的图象经过定点（﹣1，3），∴m＝﹣1，n＝3．‎ ‎∵函数g（x）＝mx2﹣2bx+n＝﹣x2﹣2bx+3 在[1，+∞）上单调递减，‎ ‎∴＝﹣b≤1，∴b≥﹣1，故选：B．‎ ‎【点评】本题主要考查对数函数的图象经过定点问题，二次函数的性质，属于基础题．‎ ‎11．已知x1＝1n，x2＝e，x3满足e＝lnx3，则下列各选项正确的是（　　）‎ A．x1＜x3＜x2 B．x1＜x2＜x3 C．x2＜x1＜x3 D．x3＜x1＜x2‎ ‎【分析】本题可以选择0，1两个中间值采用搭桥法处理．‎ ‎【解答】解：依题意，因为y＝lnx为（0，+∞）上的增函数，所以x1＝1n＜ln1＝0；‎ 应为y＝ex为R上的增函数，且ex＞0，所以0＜x2＝e，＜e0＝1；‎ x3满足e＝lnx3，所以x3＞0，所以＞0，‎ 所以lnx3＞0＝ln1，又因为y＝lnx为（0，+∞）的增函数，‎ 所以x3＞1，综上：x1＜x2＜x3．故选：B．‎ ‎【点评】本题考查了指数函数，对数函数的单调性，函数值的大小比较等，属于中档题．‎ ‎12．设且 ，函数在上是增函数，则的取值范围（ ） ‎ A．或 B．或 ‎ C．或 D．或 解析：令，则，所以的图像如图所示 当时，由复合函数的单调性可知，区间落在 ‎ 或上，所以或，故有 ‎ 当时，由复合函数的单调性可知，‎ 所以且解得，综上所述或，故选A 二．填空题（共4小题）‎ ‎13．函数f（x）＝+lg（6﹣3x）的定义域为　[﹣1，2）　．‎ ‎【解答】解：要使函数有意义，则，得，得﹣1≤x＜2，‎ 即函数的定义域为[﹣1，2），‎ ‎【点评】本题主要考查函数定义域的求解，结合根式和对数函数的性质是解决本题的关键．‎ ‎14．f（x）为R上的奇函数，当x＞0时，f（x）＝ln（x+1）﹣x，则x＜0时，f（x）＝　﹣ln（1﹣x）﹣x　‎ ‎【解答】解：根据题意，设x＜0，则﹣x＞0，则f（﹣x）＝ln（1﹣x）+x，‎ 又由f（x）为R上的奇函数，则f（x）＝﹣f（﹣x）＝﹣ln（1﹣x）﹣x，‎ 故答案为：﹣ln（1﹣x）﹣x．‎ ‎【点评】本题考查函数的奇偶性的性质以及应用，涉及函数解析式的计算，属于基础题 ‎15．已知集合且，则_____________．‎ ‎.解析：由集合元素的互异性可知：且，所以 ‎ 所以，，故且 ‎ 所以，故 ‎ ‎16．已知函数，若定义在R上的奇函数g（x）满足g（1﹣x）＝g（1+x），且，则g（2019）＝ ‎ ‎【解答】解：∵＝，f（x）+f（﹣x）＝﹣2‎ ‎∵，‎ ‎∴＝f（2•log25）+f（﹣2•log25）＝f（x）+f（﹣x）＝﹣2‎ 又∵g（1﹣x）＝g（1+x），即g（x）＝g（2﹣x），且g（x）为奇函数，‎ ‎∴g（x）＝﹣g（﹣x）∴g（2﹣x）＝﹣g（﹣x），可知函数g（x）的周期T＝4‎ ‎∴g（2019）＝g（505×4﹣1）＝g（﹣1）＝﹣g（1）＝2‎ ‎【点评】本题考查函数奇偶性，对称性与周期性的综合运用，注意各个结论的叠加使用，属于中档偏难题．‎ 三．解答题（共6小题）‎ ‎17．计算：‎ ‎（1）‎ ‎（2）‎ ‎【解答】解：（1）原式＝；‎ ‎（2）原式＝＝‎ ‎【点评】本题考查指数和对数的运算，对数的定义，属于基础题．‎ ‎18．（本小题满分12分）记关于的不等式的解集为，不等式 的解集为．‎ ‎（1）若，求和；‎ ‎（2）若，求的取值范围．‎ ‎19‎ 19. ‎（本小题满分12分）已知函数的定义域为.‎ ‎（1）求.‎ ‎（2）当时，求的值域.‎ ‎20．（本小题满分12分）某上市股票在30天内每股的交易价格（元）与时间（天）组成有序数对，点落在图中的两条线段上；该股票在30天内的日交易量（万股）与时间（天）的部分数据如下表所示 第天 ‎4‎ ‎10‎ ‎16‎ ‎22‎ ‎（万股）‎ ‎36‎ ‎30‎ ‎24‎ ‎18‎ ‎（1）根据提供的图像，写出该种股票每股交易价格（元）与时间（天）所满足的函数关系式；‎ ‎（2）根据表中数据，写出日交易量（万股）与时间（天）的一次函数关系式；‎ ‎（3）用（万元）表示该股票日交易额，写出关于的函数关系式，并求在这30天内 第几天日交易额最大，最大值为多少？‎ ‎20. （1）当时，设 由图像可知此图像过点和，故, ‎ ‎ ‎ 同理可求当时， ‎ ‎ 4分 注：少写一个或写错一个扣2分，区间写错或没写扣1分 ‎（2）设，把所给表中任意两组数据代入可求得，‎ ‎6分 ‎（3）首先日交易额（万元）=日交易量（万股）每股交易价格（元）‎ ‎8分 当时，当时，万元9分 当时，随的增大而减小10分 故在30天中的第15天，日交易额最大为125万元. 12分 ‎20．设f（x）的定义域为R+，对任意x，y∈R+都有，且x＞1时，f（x）＜0，又．‎ ‎（1）求f（1）、f（2）；‎ ‎（2）求证：f（x）为R+上减函数；‎ ‎（3）解不等式．‎ ‎【解答】解：（1）取x＝y＝1，则f（1）＝0，∴f（）＝f（1）﹣f（2）＝﹣f（2）＝1；‎ ‎∴f（2）＝﹣1；‎ ‎（2）设x1＞x2＞0，则＞1；由已知条件得：f（x1）﹣f（x2）＝f（）＜0；‎ ‎∴f（x）在定义域（0，+∞）上单调递减；‎ ‎（3）由（1）知，，可将原不等式变成：f（x）—f（5﹣x）≥f（4），‎ ‎∴根据f（x）的单调性及定义域得：，解得0＜x≤4，‎ 原不等式的解集为：（0，4]．‎ ‎【点评】本题考查抽象函数及其应用，着重考查赋值法求值，考查函数单调性的判断与证明，属于中档题．‎ ‎22.已知函数f（x）=logm（m＞0且m≠1），‎ ‎（I）判断f（x）的奇偶性并证明；‎ ‎（II）若m=，判断在（3，+∞）的单调性并用复合函数单调性结论加以说明；‎ ‎（III）若0＜m＜1，是否存在β＞α>0，使f（x）在[α，β]的值域为 ‎[logmm（β-1），logmm（α-1）]？若存在，求出此时m的取值范围；若不存在，请说明理由．‎ ‎【答案】（Ⅰ）f（x）是奇函数（Ⅱ）见解析（Ⅲ）．‎ ‎【详解】解：（Ⅰ）f（x）是奇函数；证明如下：‎ 由解得x＜-3或x＞3，‎ 所以f（x）的定义域为（-∞，-3）∪（3，+∞），关于原点对称．‎ ‎∵=，‎ 故f（x）为奇函数/‎ ‎（Ⅱ）f（x）在（3，+∞）上单调递减 ‎（Ⅲ）由（Ⅱ）知，当0＜m＜1时，f（x）在[α，β]上单调递减．‎ 假设存在β＞α＞0，使f（x）在[α，β]的值域为[logmm（β-1），logmm（α-1）]．‎ 则有，∴．‎ 所以α，β是方程的两正根，‎ 整理得mx2+（2m-1）x-3m+3=0在（0，+∞）有2个不等根α和β．‎ 令h（x）=mx2+（2m-1）x-3m+3，则h（x）在（0，+∞）有2个零点，‎ 解得，‎ 故m的取值范围为．‎ ‎【点睛】本题考查函数奇偶性、单调性以及一元二次方程实根分布，考查数形结合思想方法以及等价转化思想方法，考查综合综合分析与求解能力，属难题.‎