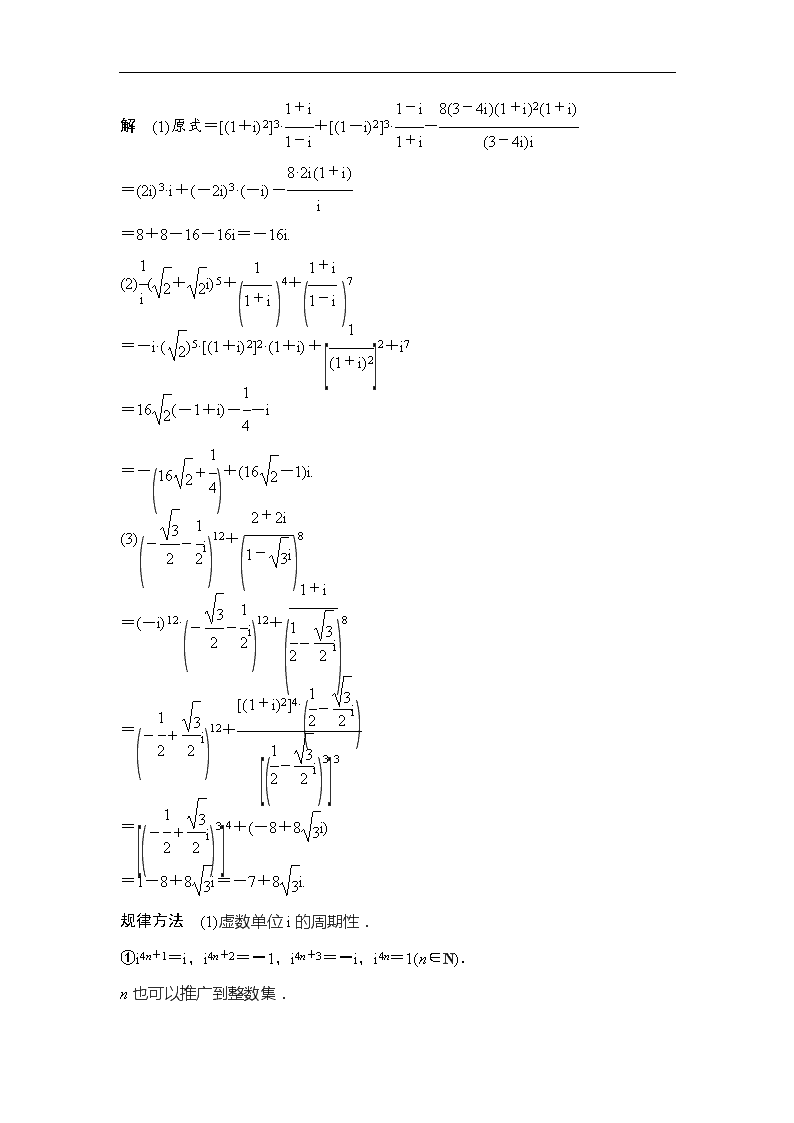高中数学选修2-2课时练习第五章 2_2 9页

‎2．2　复数的乘法与除法 ‎[学习目标]‎ ‎1．掌握复数代数形式的乘法和除法运算．‎ ‎2．理解复数乘法的交换律、结合律和乘法对加法的分配律．‎ ‎3．理解共轭复数的概念．‎ ‎[知识链接]‎ 写出下列各小题的计算结果：‎ ‎(1)(a±b)2＝________；‎ ‎(2)(‎3a＋2b)(‎3a－2b)＝________；‎ ‎(3)(‎3a＋2b)(－a－3b)＝________.‎ ‎(4)(x－y)÷(＋)＝________.‎ 答　(1)a2±2ab＋b2　(2)‎9a2－4b2‎ ‎(3)－‎3a2－11ab－6b2　(4)－ ‎[预习导引]‎ ‎1．复数的乘法 设a＋bi与c＋di分别是任意两个复数 ‎(1)定义：(a＋bi)(c＋di)＝(ac－bd)＋(ad＋bc)i.‎ ‎(2)运算律 交换律：z1·z2＝z2·z1.‎ 结合律：(z1·z2)·z3＝z1·(z2·z3)．‎ 分配律：z1(z2＋z3)＝z1z2＋z1z3.‎ ‎(3)复数的乘方 zmzn＝zm＋n，(zm)n＝zmn，(z1z2)n＝zz.‎ ‎2．共轭复数 ‎(1)定义：当两个复数的实部相等，虚部互为相反数时，这样的两个复数叫做互为共轭复数．复数z的共轭复数用表示，即若z＝a＋bi，则＝a－bi.‎ ‎(2)性质：z·＝|z|2＝||2.‎ ‎3．复数的除法 ＝＋·i.(c2＋d2≠0)‎ ‎　　　　　　　　　　　　　　　　　　　‎ 要点一　复数乘除法的运算 例1　计算：(1)(2＋i)(2－i)；　(2)(1＋2i)2‎ 解　(1)(2＋i)(2－i)＝4－i2＝4－(－1)＝5；‎ ‎(2)(1＋2i)2＝1＋4i＋(2i)2＝1＋4i＋4i2＝－3＋4i.‎ 规律方法　(1)复数的乘法可以按照多项式的乘法法则进行，注意选用恰当的乘法公式进行简便运算，例如平方差公式、完全平方公式等．‎ ‎(2)像3＋4i和3－4i这样的两个复数叫做互为共轭复数，其形态特征为a＋bi和a－bi，其数值特征为(a＋bi)(a－bi)＝a2＋b2.‎ 跟踪演练1　计算：(1)(1－2i)(3＋4i)(－2＋i)‎ ‎(2)(3＋4i)(3－4i)‎ ‎(3)(1＋i)2‎ 解　(1)(1－2i)(3＋4i)(－2＋i)＝(11－2i)(－2＋i)＝‎ ‎－20＋15i.‎ ‎(2)(3＋4i)(3－4i)＝32－(4i)2＝9－(－16)＝25.‎ ‎(3)(1＋i)2＝1＋2i＋i2＝2i.‎ 要点二　复数的乘方运算 例2　计算下列各题：‎ ‎(1)＋－；‎ ‎(2)(＋i)5＋4＋7；‎ ‎(3)12＋8.‎ 解　(1)原式＝[(1＋i)2]3·＋[(1－i)2]3·－ ‎＝(2i)3·i＋(－2i)3·(－i)－ ‎＝8＋8－16－16i＝－16i.‎ ‎(2)(＋i)5＋4＋7‎ ‎＝－i·()5·[(1＋i)2]2·(1＋i)＋2＋i7‎ ‎＝16(－1＋i)－－i ‎＝－＋(16－1)i.‎ ‎(3)12＋8‎ ‎＝(－i)12·12＋8‎ ‎＝12＋ ‎＝4＋(－8＋8i)‎ ‎＝1－8＋8i＝－7＋8i.‎ 规律方法　(1)虚数单位i的周期性．‎ ‎①i4n＋1＝i，i4n＋2＝－1，i4n＋3＝－i，i4n＝1(n∈N)．‎ n也可以推广到整数集．‎ ‎②in＋in＋1＋in＋2＋in＋3＝0(n∈N)．‎ ‎(2)记住以下结果，可提高运算速度．‎ ‎①(1＋i)2＝2i，(1－i)2＝－2i.‎ ‎②＝－i，＝i.‎ ‎③＝－i.‎ 跟踪演练2　计算＋2 004＋；‎ 解　原式＝＋1 002‎ ‎＋(4－8i＋8i－4) ‎＝i＋(－i)1 002＋0＝－1＋i.‎ 要点三　共扼复数及其应用 例3　已知复数z满足：z·＋2iz＝8＋6i，求复数z的实部与虚部的和．‎ 解　设z＝a＋bi(a，b∈R)，则z·＝a2＋b2，‎ ‎∴a2＋b2＋2i(a＋bi)＝8＋6i，‎ 即a2＋b2－2b＋2ai＝8＋6i，‎ ‎∴，‎ 解得，∴a＋b＝4，‎ ‎∴复数z的实部与虚部的和是4.‎ 规律方法　本题使用了复数问题实数化思想，运用待定系数法，化解了问题的难点．‎ 跟踪演练3　已知复数z满足|z|＝1，且(3＋4i)z是纯虚数，求z的共轭复数.‎ 解　设z＝a＋bi(a，b∈R)，则＝a－bi且|z|＝＝1，即a2＋b2＝1.①‎ 因为(3＋4i)z＝(3＋4i)(a＋bi)＝(‎3a－4b)＋(3b＋‎4a)i，而(3＋4i)z是纯虚数，‎ 所以‎3a－4b＝0，且3b＋‎4a≠0.②‎ 由①②联立，解得或 所以＝－i，或＝－＋i.‎ ‎1．复数－i＋等于(　　)　　　　　　　　　　　　　　　　　　　‎ A．－2i B.i C．0 D．2i 答案　A 解析　－i＋＝－i－＝－2i，选A.‎ ‎2．(2013·江西)已知集合M＝{1,2，zi}，i为虚数单位，N＝{3,4}，M∩N＝{4}，则复数z＝(　　)‎ A．－2i B．2i C．－4i D．4i 答案　C 解析　本题考查复数的四则运算以及集合的基本运算．因为M∩N＝{4}，所以zi＝4，设z＝a＋bi(a，b∈R)，zi＝－b＋ai，由zi＝4，利用复数相等，得a＝0，b＝－4.故选C.‎ ‎3．若复数z＝1＋i，i为虚数单位，则(1＋z)z等于(　　)‎ A．1＋3i B．3＋3i C．3－i D．3‎ 答案　A 解析　(1＋z)·z＝(2＋i)·(1＋i)＝(2×1－1)＋(2＋1)i＝1＋3i.‎ ‎4．设复数z的共轭复数是，若复数z1＝3＋4i，z2＝t＋i，且z1·2是实数，则实数t等于(　　)‎ A. B. C．－ D．－ 答案　A 解析　∵z2＝t＋i，∴2＝t－i.‎ z1·3＝(3＋4i)(t－i)＝3t＋4＋(4t－3)i，‎ 又∵z1·2∈R，∴4t－3＝0，∴t＝.‎ ‎5．复数z＝(i为虚数单位)在复平面内对应的点所在象限为(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 答案　D 解析　因为z＝＝＝，故复数z对应的点在第四象限，选D.‎ ‎1．复数代数形式的乘除运算 ‎(1)复数代数形式的乘法类似于多项式乘以多项式，复数的乘法满足交换律、结合律以及乘法对加法的分配律．‎ ‎(2)在进行复数代数形式的除法运算时，通常先将除法写成分式的形式，再把分子、分母都乘以分母的共轭复数，化简后可得，类似于以前学习的分母有理化．‎ ‎2．共轭复数的性质可以用来解决一些复数问题．‎ ‎3．复数问题实数化思想．‎ 复数问题实数化是解决复数问题的基本思想方法，其桥梁是设复数z＝a＋bi(a，b∈R)，利用复数相等的充要条件转化．‎ 一、基础达标 ‎1．设复数z满足iz＝1，其中i为虚数单位，则z等于(　　)　　　　　　　　　　　　　　　　　　　‎ A．－i B．i C．－1 D．1‎ 答案　A 解析　z＝＝－i.‎ ‎2．i为虚数单位，＋＋＋等于(　　)‎ A．0 B．2i C．－2i D．4i 答案　A 解析　＝－i，＝i，＝－i，＝i，∴＋＋＋＝0.‎ ‎3．若a，b∈R，i为虚数单位，且(a＋i)i＝b＋i，则(　　)‎ A．a＝1，b＝1 B．a＝－1，b＝1‎ C．a＝－1，b＝－1 D．a＝1，b＝－1‎ 答案　D 解析　∵(a＋i)i＝－1＋ai＝b＋i，∴.‎ ‎4．在复平面内，复数＋(1＋i)2对应的点位于(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 答案　B 解析　＋(1＋i)2＝＋i＋(－2＋2i)＝－＋i，对应点 在第二象限．‎ ‎5．设复数i满足i(z＋1)＝－3＋2i(i为虚数单位)，则z的实部是________．‎ 答案　1‎ 解析　由i(z＋1)＝－3＋2i得到z＝－1＝2＋3i－1＝1＋3i.‎ ‎6．复数的虚部是________．‎ 答案　－ 解析　原式＝＝＝－i，‎ ‎∴虚部为－.‎ ‎7．计算：(1)＋2 010；‎ ‎(2)(4－i5)(6＋2i7)＋(7＋i11)(4－3i)．‎ 解　(1)＋2 010＝＋1 005‎ ‎＝i(1＋i)＋1 005＝－1＋i＋(－i)1 005‎ ‎＝－1＋i－i＝－1.‎ ‎(2)原式＝(4－i)(6－2i)＋(7－i)(4－3i)‎ ‎＝22－14i＋25－25i＝47－39i.‎ 二、能力提升 ‎8．(2013·新课标)设复数z满足(1－i)z＝2i，则z＝(　　)‎ A．－1＋i B．－1－i C．1＋i D．1－i 答案　A 解析　因为复数z满足z(1－i)＝2i，所以z＝＝＝－1＋i.‎ ‎9．(2013·山东)若复数z满足(z－3)(2－i)＝5(i为虚数单位)，则z的共轭复数为(　　)‎ A．2＋i B．2－i ‎ C．5＋i D．5－i 答案　D 解析　由(z－3)(2－i)＝5，得z＝＋3＝＋3＝＋3＝2＋i＋3＝5＋i.所以＝5－i，选D.‎ ‎10．已知z是纯虚数，是实数，那么z等于________．‎ 答案　－2i 解析　设z＝bi(b∈R，b≠0)，则＝＝＝＝＋i是实数，所以b＋2＝0，b＝－2，所以z＝－2i.‎ ‎11．(2013·山东聊城期中)已知复数z＝，若z2＋az＋b＝1＋i(a，b∈R)，求a＋b的值．‎ 解　由z＝，‎ 得z＝＝＝1－i，‎ 又z2＋az＋b＝1＋i，‎ ‎∴(1－i)2＋a(1－i)＋b＝1＋i，‎ ‎∴(a＋b)＋(－2－a)i＝1＋i，‎ ‎∴a＋b＝1.‎ ‎12．已知复数z的共轭复数为，且z·－3iz＝，求z.‎ 解　设z＝a＋bi(a，b∈R)，则＝a－bi.‎ 又z·－3iz＝，‎ ‎∴a2＋b2－3i(a＋bi)＝，‎ ‎∴a2＋b2＋3b－3ai＝1＋3i，‎ ‎∴ ‎∴或.‎ ‎∴z＝－1，或z＝－1－3i.‎ 三、探究与创新 ‎13．已知1＋i是方程x2＋bx＋c＝0的一个根(b、c为实数)．‎ ‎(1)求b，c的值；‎ ‎(2)试说明1－i也是方程的根吗？‎ 解　(1)因为1＋i是方程x2＋bx＋c＝0的根，‎ ‎∴(1＋i)2＋b(1＋i)＋c＝0，‎ 即(b＋c)＋(2＋b)i＝0.‎ ‎∴，得.‎ ‎∴b、c的值为b＝－2，c＝2.‎ ‎(2)方程为x2－2x＋2＝0.‎ 把1－i代入方程左边得(1－i)2－2(1－i)＋2＝0，显然方程成立，∴1－i也是方程的一个根．‎