山西大学附属中学2020-2021高一数学10月模块诊断试题（Word版附答案） 6页

山西大学附中 ‎2020-2021学年高一第一学期10月（总第一次）模块诊断 数学试题 ‎ 考查时间：90分钟 考查内容:第一、二章 ‎ 一.选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．已知集合，集合，则集合（ ）‎ A． B． C． D．‎ ‎2. 下列集合表示同一集合的是（ ）‎ A. B.‎ C., D.,‎ ‎3．命题“”的否定是（ ）‎ A． B．‎ C． D．‎ ‎4.不等式的解集是 ‎ A．或 B．或 ‎ C． D．‎ ‎5. 如果实数，，满足：，则下列不等式一定成立的是（ ）‎ A． B． C． D．‎ ‎6.设全集是实数集,,则图中阴影部分所表示的集合是( )‎ A. B. C. D. ‎ ‎7．设集合，则满足条件的集合的个数是（ ）.‎ A．1 B．3 C．2 D．4‎ ‎8.已知不等式的解集是，则的值为（ ）．‎ A．1 B． C．0 D．‎ ‎9．设集合， ，若，则的取值范围是（ ）‎ A． B． C． D．‎ ‎10．命题“，”为真命题的一个充分不必要条件是（ ）‎ A． B． C. D．‎ ‎11．已知，，，则的最小值为（ ）‎ A．16 B．4 C． D．‎ ‎12.已知集合,.若,则实数的取值范围是（ ）‎ A. B. C. D.‎ 二、填空题（每题4分，满分16分，将答案填在答题纸上）‎ ‎13. 设集合，若,则的值为 .‎ ‎14.“不等式在上恒成立”的充要条件是 .‎ ‎15.若，则的最小值等于 .‎ ‎16.已知,,若,则实数的取值范围为 .‎ 三、解答题（本大题共4小题，共48分）‎ ‎17. 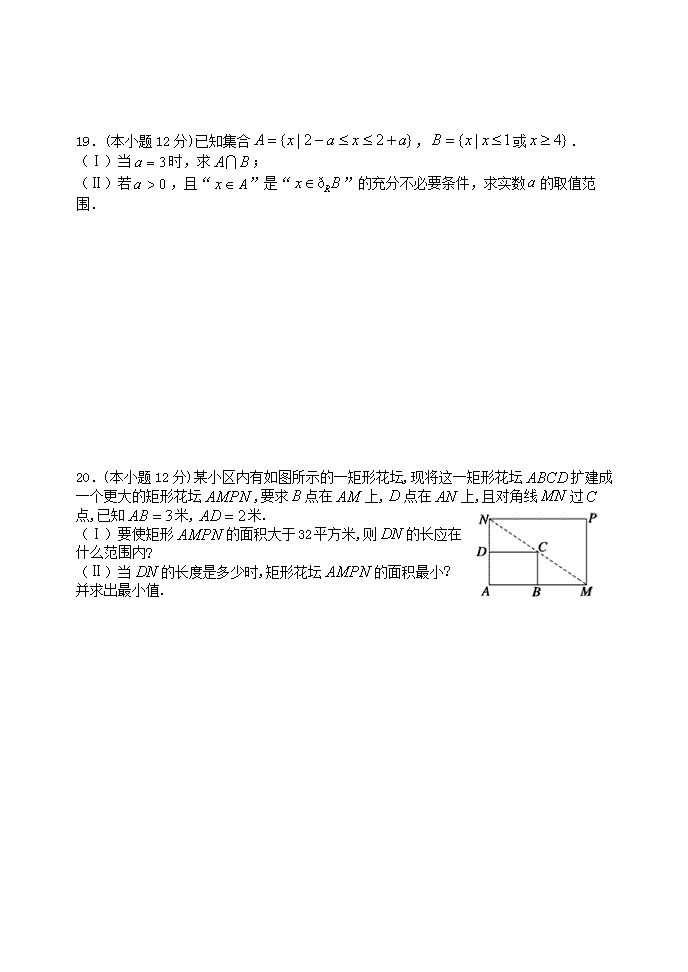(本小题12分)已知集合,集合.‎ ‎（Ⅰ）当时,求;‎ ‎（Ⅱ）若,求实数的取值范围;‎ ‎18．(本小题12分)设集合，．‎ ‎（Ⅰ）若，求实数的值；‎ ‎（Ⅱ）若，求实数的取值范围．‎ ‎19．(本小题12分)已知集合，或．‎ ‎（Ⅰ）当时，求；‎ ‎（Ⅱ）若，且“”是“”的充分不必要条件，求实数的取值范围．‎ ‎20．(本小题12分)某小区内有如图所示的一矩形花坛,现将这一矩形花坛扩建成一个更大的矩形花坛,要求点在上,点在上,且对角线过点,已知米,米.‎ ‎（Ⅰ）要使矩形的面积大于32平方米,则的长应在什么范围内?‎ ‎（Ⅱ）当的长度是多少时,矩形花坛的面积最小?并求出最小值.‎ 山西大学附中 ‎2020-2021学年高一第一学期10月（总第一次）月考 数学评分细则 ‎ 考查时间：90分钟 考查内容:第一、二章 ‎ 一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求.）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ A B A D D C D C D A C D 二．填空题（本题共4小题，每小题4分，共16分.）‎ ‎13. 14. ‎ ‎15.8 16. ‎ ‎17.已知集合,集合.‎ ‎（1）当时,求;‎ ‎（2）若,求实数的取值范围;‎ 解:（1）当时,.‎ ‎∴;‎ ‎（2）∵,∴,则有:‎ ‎,解之得:≤.‎ ‎∴实数的取值范围是;‎ ‎18．设集合，．‎ ‎（Ⅰ）若，求实数的值；‎ ‎（Ⅱ）若，求实数的取值范围．‎ ‎【解析】（Ⅰ），，‎ ‎，且，‎ 所以，，解得；‎ ‎（Ⅱ），，则或，‎ 又，所以，解得.‎ 因此，实数的取值范围是．‎ ‎19．已知集合，或．‎ ‎（1）当时，求；‎ ‎（2）若，且“”是“”的充分不必要条件，求实数a的取值范围．‎ ‎【详解】‎ ‎（1）∵当时，，或，‎ ‎∴或；‎ ‎（2）∵或，∴，‎ 由“”是“”的充分不必要条件得A是的真子集，且，‎ 又，∴，∴．‎ ‎20．某小区内有如图所示的一矩形花坛,现将这一矩形花坛扩建成一个更大的矩形花坛,要求点在上,点在上,且对角线过点,已知米,米.‎ ‎（Ⅰ）要使矩形的面积大于32平方米,则的长应在什么范围内?‎ ‎（Ⅱ）当的长度是多少时,矩形花坛的面积最小?并求出最小值.‎ 解析：（Ⅰ）设的长为米，则米 ‎∵，‎ ‎∴∴‎ 由得 又得 解得：或 即的长取值范围是.‎ ‎（Ⅱ）矩形花坛的面积为 当且仅当，即时，矩形花坛的面积最小为平方米．‎