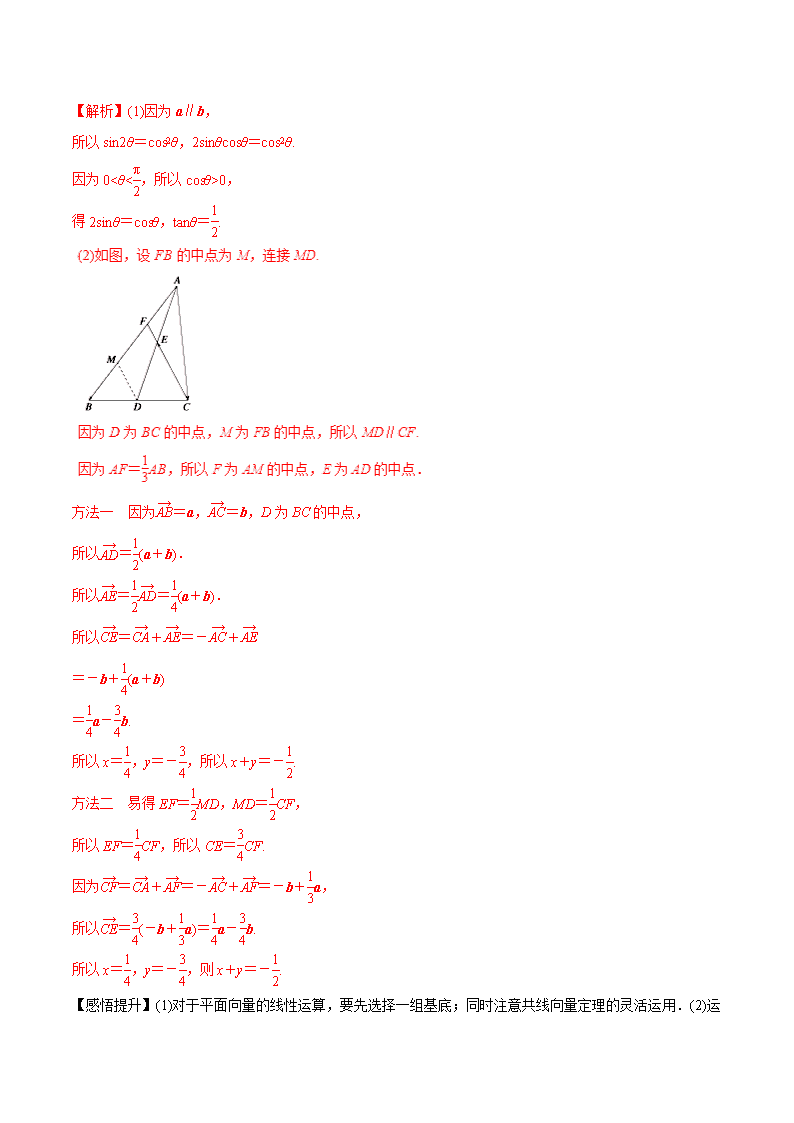【数学】2020届一轮复习人教A版平面向量与复数学案 15页

‎【考向解读】 ‎ ‎1.命题角度：复数的四则运算和几何意义；以平面图形为背景，考查平面向量的线性运算、平面向量的数量积.‎ ‎2.题目难度：复数题目为低档难度，平面向量题目为中低档难度.‎ ‎【命题热点突破一】平面向量的线性运算 ‎(1)在平面向量的化简或运算中，要根据平面向量基本定理选好基底，变形要有方向不能盲目转化；‎ ‎(2)在用三角形加法法则时要保证“首尾相接”，结果向量是第一个向量的起点指向最后一个向量终点所在的向量；在用三角形减法法则时要保证“同起点”，结果向量的方向是指向被减向量．‎ 例1、(2018·全国Ⅰ)在△ABC中，AD为BC边上的中线，E为AD的中点，则等于(　　)‎ A.－ B.－ C.＋ D.＋ 答案　A 解析　作出示意图如图所示.‎ ＝＋＝＋＝×(＋)＋(－)＝－.‎ 故选A. ‎ ‎【方法技巧】‎ ‎(1)向量加法的平行四边形法则：共起点；三角形法则：首尾相连；向量减法的三角形法则：共起点连终点，指向被减.‎ ‎(2)已知O为平面上任意一点，则A，B，C三点共线的充要条件是存在s，t，使得＝s＋t，且s＋t＝1，s，t∈R.‎ ‎(3)证明三点共线问题，可转化为向量共线解决.‎ ‎【变式探究】【2017课标1，理13】已知向量a，b的夹角为60°，|a|=2，|b|=1，则| a +2 b |= .‎ ‎【答案】‎ ‎【解析】利用如下图形，可以判断出的模长是以2为边长的菱形对角线的长度，‎ 所以.‎ ‎【变式探究】如图，在△ABC中，N是AC边上一点，且＝，P是BN上的一点，若＝m＋，则实数m的值为(　　)‎ A. B. C.1 D.3‎ 答案　B 解析　∵＝，∴＝，‎ ‎∴＝m＋＝m＋.‎ 又B，N，P三点共线，∴m＋＝1，∴m＝.‎ ‎【变式探究】(1)设0<θ<，向量a＝(sin2θ，cosθ)，b＝(cosθ，1)，若a∥b，则tanθ＝______.‎ ‎(2)如图，在△ABC中，AF＝AB，D为BC的中点，AD与CF交于点E.若＝a，＝b，且＝xa＋yb，则x＋y＝________.‎ ‎【答案】(1)　(2)－ ‎【解析】(1)因为a∥b，‎ 所以sin2θ＝cos2θ，2sinθcosθ＝cos2θ.‎ 因为0<θ<，所以cosθ>0，‎ 得2sinθ＝cosθ，tanθ＝.‎ 方法一　因为＝a，＝b，D为BC的中点，‎ 所以＝(a＋b)．‎ 所以＝＝(a＋b)．‎ 所以＝＋＝－＋ ‎＝－b＋(a＋b)‎ ‎＝a－b.‎ 所以x＝，y＝－，所以x＋y＝－.‎ 方法二　易得EF＝MD，MD＝CF，‎ 所以EF＝CF，所以CE＝CF.‎ 因为＝＋＝－＋＝－b＋a，‎ 所以＝(－b＋a)＝a－b.‎ 所以x＝，y＝－，则x＋y＝－.‎ ‎【感悟提升】(1)对于平面向量的线性运算，要先选择一组基底；同时注意共线向量定理的灵活运用．(2)‎ 运算过程中重视数形结合，结合图形分析向量间的关系．‎ ‎【变式探究】如图，在正方形ABCD中，M，N分别是BC，CD的中点，若＝λ＋μ，则λ＋μ等于(　　)‎ A.2 B.　C. D. 答案　D 解析　方法一　如图以AB，AD为坐标轴建立平面直角坐标系，设正方形边长为1，＝，＝，＝(1，1).‎ ‎∵＝λ＋μ＝λ＋μ＝，‎ ‎∴解得故λ＋μ＝.‎ 方法二　以，作为基底，‎ ‎∵M，N分别为BC，CD的中点，‎ ‎∴＝＋＝＋，＝＋＝－，‎ ‎∴＝λ＋μ＝＋，‎ 又＝＋，‎ 因此解得所以λ＋μ＝.‎ ‎【命题热点突破二】平面向量的数量积 ‎(1)数量积的定义：a·b＝|a||b|cosθ.‎ ‎(2)三个结论 ‎①若a＝(x，y)，则|a|＝＝.‎ ‎②若A(x1，y1)，B(x2，y2)，则 ‎||＝.‎ ‎③若a＝(x1，y1)，b＝(x2，y2)，θ为a与b的夹角，‎ 则cosθ＝＝.‎ 例2、（2018年天津卷）如图，在平面四边形ABCD中，，，，. 若点E为边CD上的动点，则的最小值为 ‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】建立如图所示的平面直角坐标系，则，，，，‎ 点在上，则，设，则：‎ ‎，即，‎ 据此可得：，且：‎ ‎，，‎ 由数量积的坐标运算法则可得：‎ ‎，‎ 整理可得：，‎ 结合二次函数的性质可知，当时，取得最小值.‎ 本题选择A选项. ‎ ‎【命题热点突破四】复数的概念与运算 复数运算的重点是除法运算，其关键是进行分母实数化，分子分母同时乘分母的共轭复数．对一些常见的运算，如(1±i)2＝±2i，＝i，＝－i等要熟记．‎ 例4、(2018·全国Ⅰ)设z＝＋2i，则|z|等于(　　)‎ A.0 B. C.1 D. 答案　C 解析　∵z＝＋2i＝＋2i＝＋2i＝i，‎ ‎∴|z|＝1.故选C.‎ ‎【变式探究】【2017山东，理2】已知,i是虚数单位，若，则a=‎ ‎（A）1或-1 （B） （C）- （D）‎ ‎【答案】A ‎【解析】由得，所以，故选A.‎ ‎【变式探究】已知，i是虚数单位，若，则的值为_______.‎ ‎【答案】2‎ ‎【解析】由，可得，所以，，故答案为2．‎ ‎【变式探究】(1)若复数z＝，则|z|＝(　　)‎ A． B． C．1 D．2‎ ‎(2)已知复数z＝(i为虚数单位)，则复数z在复平面内对应的点在(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【答案】(1)C　(2)B　‎ ‎【解析】 (1)z＝＝＝－i，，所以|z|＝＝1.‎ ‎(2)z＝＝－1－i，则复数z＝－1＋i，对应的点在第二象限．‎ ‎【高考真题解读】‎ ‎1. （2018年浙江卷）已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为，向量b满足b2−4e·b+3=0，则|a−b|的最小值是 A. −1 B. +1 C. 2 D. 2−‎ ‎【答案】A ‎【解析】设，则由得，‎ 由得 因此的最小值为圆心到直线的距离减去半径1，为选A.‎ ‎2. （2018年天津卷）如图，在平面四边形ABCD中，，，，. 若点E为边CD上的动点，则的最小值为 ‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】建立如图所示的平面直角坐标系，则，，，，‎ 点在上，则，设，则：‎ ‎，即，‎ 据此可得：，且：‎ ‎，，‎ 由数量积的坐标运算法则可得：‎ ‎，‎ 整理可得：，‎ 结合二次函数的性质可知，当时，取得最小值.‎ 本题选择A选项.‎ ‎3. （2018年全国I卷理数）设抛物线C：y2=4x的焦点为F，过点（–2，0）且斜率为的直线与C交于M，N两点，则=‎ A. 5 B. 6 C. 7 D. 8‎ ‎【答案】D ‎【解析】根据题意，过点（–2，0）且斜率为的直线方程为，与抛物线方程联立，消元整理得：，解得，又，所以，从而可以求得，故选D.‎ ‎4. （2018年全国I卷理数）在△中，为边上的中线，为的中点，则 A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】根据向量的运算法则，可得 ‎，‎ 所以，故选A.‎ ‎5. （2018年全国Ⅱ卷理数）已知向量，满足，，则 A. 4 B. 3 C. 2 D. 0‎ ‎【答案】B ‎【解析】因为 所以选B.‎ ‎6. （2018年江苏卷）在平面直角坐标系中，A为直线上在第一象限内的点，，以AB为直径的圆C与直线l交于另一点D．若，则点A的横坐标为________． ‎ ‎5.【2017天津，理13】在中，，，.若，，且，则的值为___________.‎ ‎【答案】 ‎ ‎【解析】,则 ‎.‎ ‎6.【2017山东，理12】已知是互相垂直的单位向量，若与的夹角为，则实数的值是 .‎ ‎【答案】‎ ‎【解析】，‎ ‎，‎ ‎，‎ ‎，解得：．‎ ‎7．【2017浙江，15】已知向量a，b满足则的最小值是________，最大值是_______．‎ ‎【答案】4，‎ ‎【解析】设向量的夹角为，由余弦定理有：，‎ ‎，则：‎ ‎，‎ 令，则，‎ 据此可得：，‎ 即的最小值是4，最大值是．‎ ‎8.【2017浙江，10】如图，已知平面四边形ABCD，AB⊥BC，AB＝BC＝AD＝2，CD＝3，AC与BD 交于点O，记，，，则 A． B． C． D．‎ ‎【答案】C ‎【解析】因为， ， ，所以，故选C。‎ ‎9.【2017江苏，12】如图,在同一个平面内，向量,,的模分别为1,1,,与的夹角为,且tan=7,与的夹角为45°.若, 则 ▲ .‎ ‎ ‎ A ‎ C ‎ B O ‎(第12题) ‎ ‎【答案】3 ‎ ‎10.【2017江苏，16】 已知向量 ‎（1）若a∥b,求x的值；‎ ‎（2）记,求的最大值和最小值以及对应的的值.‎ ‎【答案】（1）（2）时，取得最大值，为3； 时，取得最小值，为.‎ ‎【解析】‎ 解：（1）因为，，a∥b，‎ ‎ 所以.‎ 若，则，与矛盾，故.‎ 于是. ‎ 又，所以.‎ ‎（2）.‎ 因为，所以，‎ 从而.‎ 于是，当，即时， 取到最大值3；‎ 当，即时， 取到最小值.‎ ‎1.【2017课标1，理3】设有下面四个命题 ‎：若复数满足，则；：若复数满足，则；‎ ‎：若复数满足，则；：若复数，则.‎ 其中的真命题为 A. B． C． D．‎ ‎【答案】B ‎【解析】令，则由得，所以，故正确；‎ 当时，因为，而知，故不正确；‎ 当时，满足，但，故不正确；‎ 对于，因为实数的共轭复数是它本身，也属于实数，故正确，故选B.‎ ‎2.【2017课标II，理1】（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由复数除法的运算法则有：，故选D。‎ ‎3.【2017山东，理2】已知,i是虚数单位，若，则a=‎ ‎（A）1或-1 （B） （C）- （D）‎ ‎【答案】A ‎【解析】由得，所以，故选A. ‎ ‎3.【2016高考新课标2理数】已知在复平面内对应的点在第四象限，则实数的取值范围是（ ）‎ ‎（A） （B） （C） （D）‎ ‎【答案】A ‎【解析】要使复数对应的点在第四象限应满足：，解得，故选A.‎ ‎4.【2016年高考北京理数】设，若复数在复平面内对应的点位于实轴上，则_______________.‎ ‎【答案】－1‎ ‎【解析】，故填：－1‎ ‎5.【2016高考山东理数】若复数z满足其中i为虚数单位，则z=（ ）‎ ‎（A）1+2i （B）12i （C） （D）‎ ‎【答案】B ‎【解析】设，则，故，则，选B.‎ ‎6.【2016高考天津理数】已知，i是虚数单位，若，则的值为_______.‎ ‎【答案】2‎ ‎【解析】由，可得，所以，，故答案为2．‎ ‎7.【2016高考江苏卷】复数其中i为虚数单位，则z的实部是________▲________. ‎ ‎【答案】5‎ ‎【解析】，故z的实部是5‎ ‎1．(2015·新课标全国Ⅱ，2)若a为实数，且(2＋ai)(a－2i)＝－4i，则a＝(　　)‎ A．－1 B．0 C．1 D．2‎ ‎2．(2015·广东，2)若复数z＝i(3－2i)(i是虚数单位)，则z＝(　　)‎ A．3－2i B．3＋2i C．2＋3i D．2－3i 解析　因为z＝i(3－2i)＝2＋3i，所以z＝2－3i，故选D.‎ 答案　D ‎3．(2015·四川，2)设i是虚数单位，则复数i3－＝(　　)‎ A．－i B．－3i C．i D．3i 解析　i3－＝－i－＝－i＋2i＝i.选C.‎ 答案　C ‎4．(2015·山东，2)若复数z满足＝i，其中i为虚数单位，则z＝(　　)‎ A．1－i B．1＋i C．－1－i D．－1＋i 解析　∵＝i，∴z＝i(1－i)＝i－i2＝1＋i，∴z＝1－i.‎ 答案　A ‎5．(2015·新课标全国Ⅰ，1)设复数z满足＝i，则|z|＝(　　)‎ A．1 B. C. D．2‎ 解析　由＝i，得1＋z＝i－zi，z＝＝i，∴|z|＝|i|＝1.‎ 答案　A