河北省保定一中2020届高三上学期阶段测试数学理科试卷 9页

保定一中2019-2020学年第一学期高三年级第二次阶段考试 理科数学试卷 命题人 ：霍云超 周改 审定人：霍云超 周改 说明：‎ ‎1.本试卷有选择题和非选择题两部分构成，其中选择题分，非选择题分，总分分. 考试时间分钟. ‎ ‎2. 每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑. 如需改动，用橡皮擦干净后，再选涂其他答案标号. ‎ ‎3．考试过程中考生答题必须使用毫米黑色水笔作答，答案必须写在指定的答题区域，在其它区域作答无效. ‎ 第Ⅰ卷 选择题（60分）‎ 一、选择题（本大题有12个小题，每小题5分. 在每小题给出的四个选项中，只有一项是符合要求）‎ ‎1．设集合.则=( )‎ A. B. C. D.‎ ‎2．复数（是虚数单位）在复平面上对应的点位于（ ）．‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3．下列函数中，既是偶函数又在区间(0，＋∞)上单调递增的是(　　)‎ A. B. C. D. ‎ ‎4．已知函数，若，，，则，，的大小关系为（ ）‎ A. B. C. 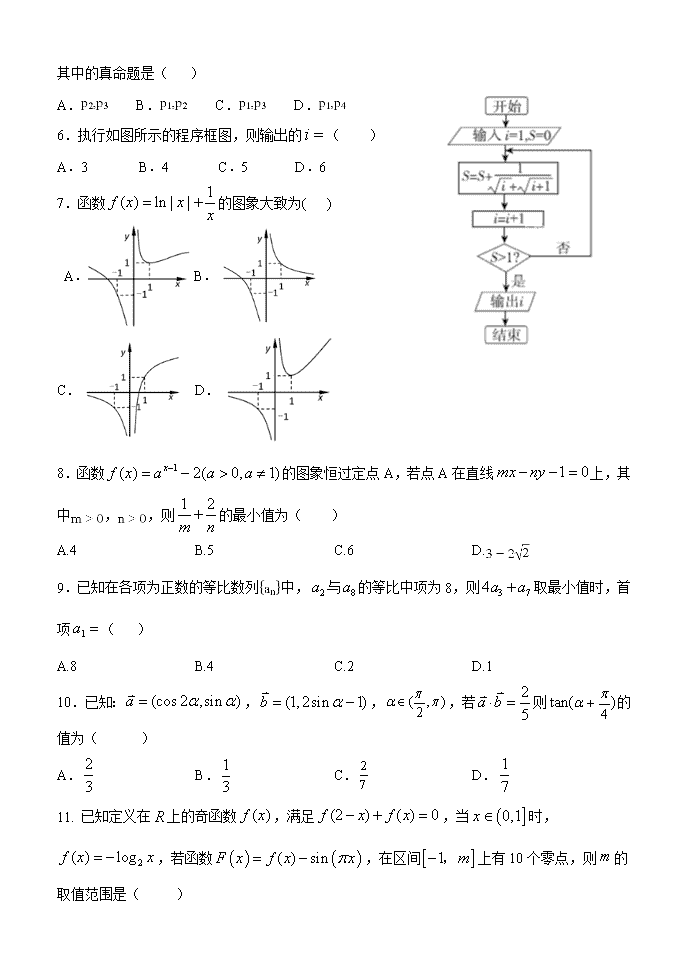D.‎ ‎5．不等式组的解集为D,有下面四个命题：‎ ‎，，‎ ‎ ，‎ 其中的真命题是（ ）‎ A． B． C． D．‎ ‎6．执行如图所示的程序框图，则输出的（ ）‎ A．3 B．‎4 C．5 D．6‎ ‎7．函数的图象大致为( )‎ ‎ A．B．‎ C． D．‎ ‎8．函数的图象恒过定点A，若点A在直线上，其中，，则的最小值为（ ）‎ A.4 B‎.5 ‎C.6 D.‎ ‎9．已知在各项为正数的等比数列中，与的等比中项为8，则取最小值时，首项（ ）‎ A.8 B‎.4 ‎C.2 D.1‎ ‎10．已知：，，，若则的值为（ ）‎ A． B． C． D．‎ ‎11. 已知定义在上的奇函数，满足，当时，，若函数，在区间上有10个零点，则的取值范围是（ ）‎ A． B． C． D．‎ ‎ ‎ 第Ⅱ卷 非选择题（90分）‎ 二、填空题（本大题共4小题，每小题5分，共20分.）‎ ‎13．若对任意的，不等式恒成立，则实数的取值范围为________.‎ ‎14．已知两个单位向量e1，e2的夹角为，若向量b1＝e1－2e2，b2＝3e1＋4e2，则b1·b2＝________‎ ‎15.已知分别为三个内角的对边，，且，则面积的最大值为____________．‎ ‎16．已知函数若对任意，总存在，使得成立，则实数a的值为____．‎ 三、解答题（本大题共6小题，共70分.）‎ ‎17.(本小题满分10分) 已知函数f(x)＝Asin(ωx＋φ)，x∈R(其中A>0，ω>0,0<φ<)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为 ‎(1)求函数f(x)的解析式.（2）写出函数f(x)的单调递增区间.‎ ‎(3)当x∈时，求f(x)的值域.‎ ‎18．(本小题满分12分)已知分别为的三内角A，B，C的对边，其面积，在等差数列中，，公差．数列的前n项和为，且．‎ ‎（1）求数列的通项公式；‎ ‎（2）若，求数列的前n项和．‎ ‎19．(本小题满分12分)定义：已知函数在上的最小值为t，若恒成立，则称函数在上具有“”性质．‎ ‎（）判断函数在上是否具有“”性质？说明理由．‎ ‎（）若在上具有“”性质，求的取值范围．‎ ‎20．(本小题满分12分)已知函数．‎ ‎（1）当a为何值时，x轴为曲线的切线；‎ ‎（2）设函数，讨论在区间（0，1）上零点的个数．‎ ‎21．(本小题满分12分)已知函数.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）设，记，证明：.‎ ‎22. (本小题满分12分)已知函数，其中无理数.‎ ‎（1）若函数有两个极值点，求的取值范围；‎ ‎（2）若函数的极值点有三个，最小的记为，最大的记为，若的最大值为，求的最小值.‎ 保定一中2019-2020学年第一学期高三年级第二次阶段考试 理科数学试卷答案 ABBDB CADCD AD , -6, , ‎ ‎11. 由可知函数的图象关于点成中心对称，‎ 且，所以，，所以，函数的周期为，‎ 由于函数为奇函数，则，则，‎ 作出函数与函数的图象如下图所示：‎ ‎,，‎ 于是得出，，‎ 由图象可知，函数与函数在区间上从左到右个交点的横坐标分别为、、、、、、、、、，第个交点的横坐标为，‎ 因此，实数的取值范围是，故选：A。‎ ‎12. ‎ ‎17.‎ ‎18. （1）SacsinBac•，∴ac＝4，又，＝，‎ ‎∴，∴b＝2，从而＝⇒∴,‎ 故可得：，∴＝2+2（n﹣1）＝2n；∵，∴当n＝1时，，‎ 当n≥2时，，两式相减，得，（n≥2）∴数列{}为等比数列，‎ ‎∴． ‎ ‎（2）由（1）得，∴＝• +•+…+•＝1×21+2×21+3×21+…+，∴2＝1×22+2×23+3×24+…+n2n+1，‎ ‎∴﹣＝1×21+（22+23+…+2n）﹣n2n+1， 即：﹣＝（1-n）2n+1-2，‎ ‎∴＝（n﹣1）2n+1+2.‎ ‎19.试题解析：（）∵，，对称轴，开口向上，‎ 当时，取得最小值为，∴，∴函数在上具有“”性质．‎ ‎（），，其图象的对称轴方程为．‎ ① 当，即时，．‎ 若函数具有“”性质，则有总成立，即．‎ ‎②当，即时，．‎ 若函数具有“”性质，则有总成立，解得无解．‎ ‎③当，即时，，若函数具有“”性质，‎ 则有，解得无解．‎ 综上所述，若在上具有“”性质，则．‎ ‎20.（1）的导数为，‎ 设切点为，可得，即，‎ 解得；‎ ‎（2），‎ 当时，，在（0，1）递增，可得，，有一个零点；‎ 当时，，在（0，1）递减，，‎ 在（0，1）无零点；‎ 当时，在（0，）递增，在（，1）递减，‎ 可得在（0，1）的最大值为，‎ ‎①若＜0，即，在（0，1）无零点；‎ ‎②若=0，即，在（0，1）有一个零点；‎ ‎③若＞0，即，‎ 当时，在（0，1）有两个零点；当时，在（0，1）有一个零点；‎ 综上可得，a＜时，在（0，1）无零点；当a=或a≥时，在（0，1）有一个零点；当＜a＜时，在（0，1）有两个零点．‎ ‎21，（1） 不等式即为，即上述不等式同解于，即①，或，即②，或，即③， 由①②③得不等式的解集为或 ‎（2） ‎ ‎ ‎ ‎ ‎ 在区间上是增函数 ‎ ‎22.解：（Ⅰ），‎ 令，，‎ ‎∵有两个极值点 ‎∴ 有两个不等的正实根 ‎∵‎ ‎∴当时，，在上单调递增，不符合题意．‎ 当时，当时，，当时，，‎ ‎∴在上单调递减，在上单调递增．‎ 又∵，当→时，→‎ ‎∴‎ ‎∴‎ 综上，的取值范围是．‎ ‎（Ⅱ）．‎ ‎∵有三个极值点 ‎∴有三个零点，1为一个零点，其他两个则为的零点，由（Ⅰ）知.‎ ‎∵‎ ‎∴的两个零点即为的最小和最大极值点，，即.‎ ‎∴令，由题知.‎ ‎∴，，‎ ‎∴‎ 令，，则，令，则．‎ ‎∴在上单调递增∴∴在上单调递减 ‎∴故的最小值为．‎