高一必修1典例选讲及配套习题 第16讲 对数函数 4页

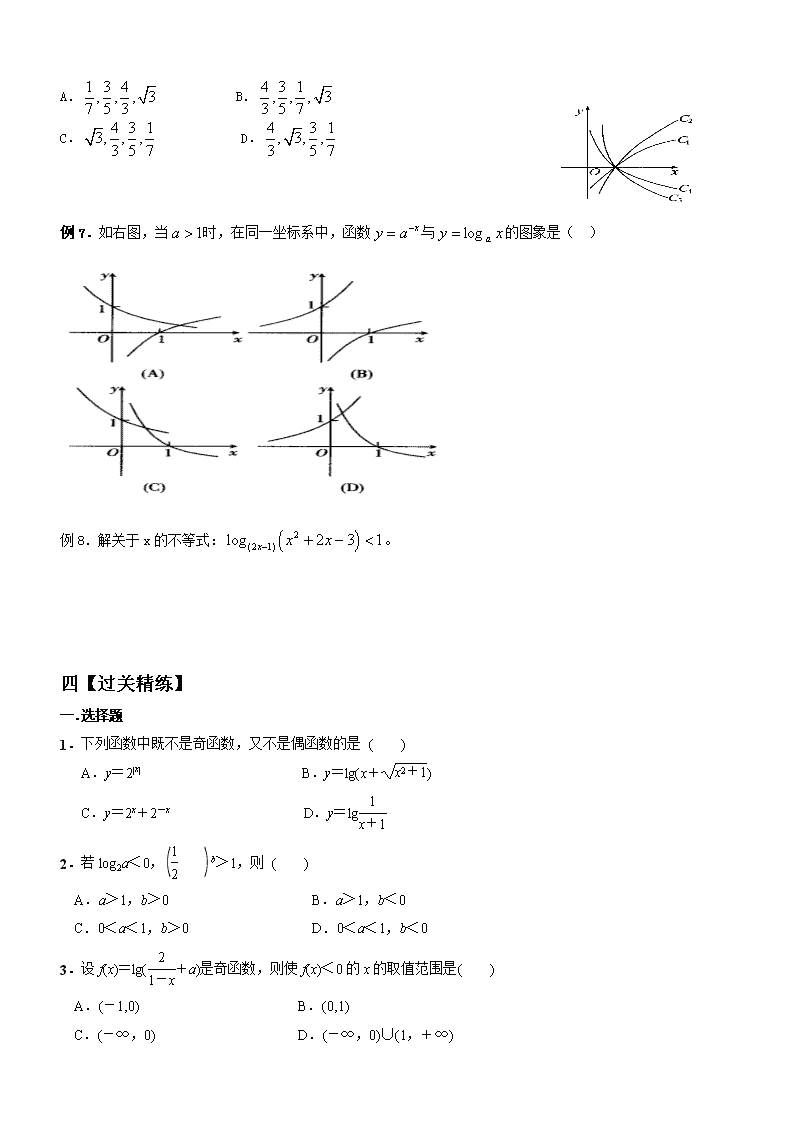
第16讲 对数函数 一【学习目标】‎ ‎1．理解对数函数的概念；‎ ‎2．掌握对数函数的图像和性质；‎ ‎3．对数函数性质的应用。‎ 二【典例精析】‎ 例1．求下列函数的定义域：‎ ‎（1） (2)y= ‎ 例2．求下列函数的值域：‎ ‎（1） （2）‎ 例3．比较大小：‎ ‎（1） （2）（ 3）‎ ‎（4） （5）‎ 例4． 求函数的单调区间 例5．已知函数 ‎ ‎（1）若函数的定义域为R，求实数a的取值范围；‎ ‎（2）若函数的值域为R，求实数a的取值范围；‎ ‎（3）若函数在内为增函数，求实数a的取值范围 例6．如图中曲线是对数函数的图象，已知值取，则对应于的值依次为（　　　）‎ A．　 B．‎ C．　　 D．‎ 例7．如右图，当时，在同一坐标系中，函数与的图象是（　）‎ 例8．解关于x的不等式：。‎ 四【过关精练】‎ 一.选择题 ‎1．下列函数中既不是奇函数，又不是偶函数的是 (　　)‎ ‎ A．y＝2|x| B．y＝lg(x＋) ‎ ‎ C．y＝2x＋2－x D．y＝lg ‎2．若log2a＜0，b＞1，则 (　　)‎ A．a＞1，b＞0 B．a＞1，b＜0‎ C．0＜a＜1，b＞0 D．0＜a＜1，b＜0‎ ‎3．设f(x)＝lg(＋a)是奇函数，则使f(x)＜0的x的取值范围是(　　)‎ A．(－1,0) B．(0,1)‎ C．(－∞，0) D．(－∞，0)∪(1，＋∞)‎ ‎ ‎ ‎4．设a＝log2，b＝log，c＝0.3，则 (　　)‎ A．a＜b＜c B．a＜c＜b C．b＜c＜a D．b＜a＜c ‎ ‎ ‎5．已知函数f(x)＝ax＋logax(a＞0且a≠1)在[1,2]上的最大值与最小值之和为 ‎ loga2＋6，则a的值为 (　　)‎ ‎ A. B. C．2 D．4‎ ‎ ‎ 二.填空题 ‎6．计算：[(－4)3]＋log525＝________.‎ ‎ ‎ ‎7．已知集合A＝{x|log2x≤2}，B＝(－∞，a)，若A⊆B，则实数a的取值范 ‎ 围是(c，＋∞)，其中c＝________.‎ ‎ ‎ ‎8．函数y＝log3(x2－2x)的单调减区间是________．‎ 三.解答题 ‎9．求值：.‎ ‎ ‎ ‎10．若函数y＝lg(3－4x＋x2)的定义域为M.当x∈M时，求f(x)＝2x＋2－3×4x的最值及相应的x 的值．‎ ‎ ‎ 第16讲部分答案 过关精炼：‎ ‎1解析：依次根据函数奇偶性定义判断知，A，C选项对应函数为偶函数，B选项对应函 ‎ 数为奇函数，只有D选项对应函数定义域不关于原点对称，故为非奇非偶函数 ‎2解析：由log2a＜0⇒0＜a＜1，由b＞1⇒b＜0.答案：D ‎3解析：∵f(x)为奇函数，∴f(0)＝0，∴a＝－1.∴f(x)＝lg，由f(x)＜0得，0＜＜1，‎ ‎ ∴－1＜x＜0. 答案：A ‎4解析：∵log2 ＜log1＝0，∴a＜0；∵log＞log＝1，∴b＞1；‎ ‎ ∵0.3＜1，∴0＜c＜1，综上知a＜c＜b.答案：B ‎5解析：∵函数f(x)＝ax＋logax(a＞0且a≠1)在[1,2]上的最值恰为两个端点的值，‎ ‎∴f(1)＋ f(2)＝a1＋loga1＋a2＋loga2＝a＋a2＋loga2＝6＋loga2，解得a＝2或a＝－3(舍去)，故应选C ‎6解析：原式＝(－4)1＋log552＝－4＋2＝－2. 答案：－2‎ ‎7解析：∵log2x≤2，∴0＜x≤4.又∵A⊆B，∴a＞4，∴c＝4. 答案：4‎ ‎8解析：令u＝x2－2x，则y＝log3u.‎ ‎ ∵y＝log3u是增函数，u＝x2－2x＞0的减区间是(－∞，0)，‎ ‎ ∴y＝log3(x2－2x)的减区间是(－∞，0)．答案：(－∞，0)‎ ‎9解：解法一：原式＝ ‎ ＝＝.‎ ‎10解：y＝lg(3－4x＋x2)，∴3－4x＋x2＞0，‎ ‎ 解得x＜1或x＞3，∴M＝{x|x＜1，或x＞3}，‎ ‎ f(x)＝2x＋2－3×4x＝4×2x－3×(2x)2.‎ ‎ 令2x＝t，∵x＜1或x＞3，∴t＞8或0＜t＜2.‎ ‎ ∴f(t)＝4t－3t2＝－32＋(t＞8或0＜t＜2)．‎ ‎ 由二次函数性质可知：‎ ‎ 当0＜t＜2时，f(t)∈，‎