2021版高考数学一轮复习核心素养测评三十七数列建模问题新人教B版 0 5页

核心素养测评三十七 数列建模问题 ‎(30分钟　60分)‎ 一、选择题(每小题5分,共20分)‎ ‎1.70周年国庆阅兵活动向全世界展示了我军威武文明之师的良好形象,展示了科技强军的伟大成就以及维护世界和平的坚定决心,在阅兵活动的训练工作中,不仅使用了北斗导航、电子沙盘、仿真系统、激光测距机、迈速表和高清摄像头等新技术装备,还通过管理中心对每天产生的大数据进行存储、分析,有效保证了阅兵活动的顺利进行,假如训练过程中第一天产生的数据量为a,其后每天产生的数据量都是前一天的q(q>1)倍,那么训练n天产生的总数据量为(　　)‎ A.aqn-1 B.aqn C. D.‎ ‎【解析】选D.训练过程中第一天产生的数据量为a,其后每天产生的数据量都是前一天的q(q>1)倍,那么训练n天产生的总数据量为:‎ Sn=a+aq+aq2+…+aqn-1=.‎ ‎2.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,若要使织布的总尺数不少于30,该女子所需的天数至少为 (　　)‎ A.10 B.9 C.8 D.7‎ ‎【解析】选C.设该女子第一天织布x尺,‎ 则=5,解得x=,‎ 所以前n天织布的尺数为(2n-1),‎ 5‎ 由(2n-1)≥30,得2n≥187,解得n的最小值为8.‎ ‎3.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:‎ 第一步:构造数列1,,,,…,.①‎ 第二步:将数列①的各项乘以,得到一个新数列a1,a2,a3,…,an.‎ 则a1a2+a2a3+a3a4+…+an-1an= (　　)‎ A. B.‎ C. 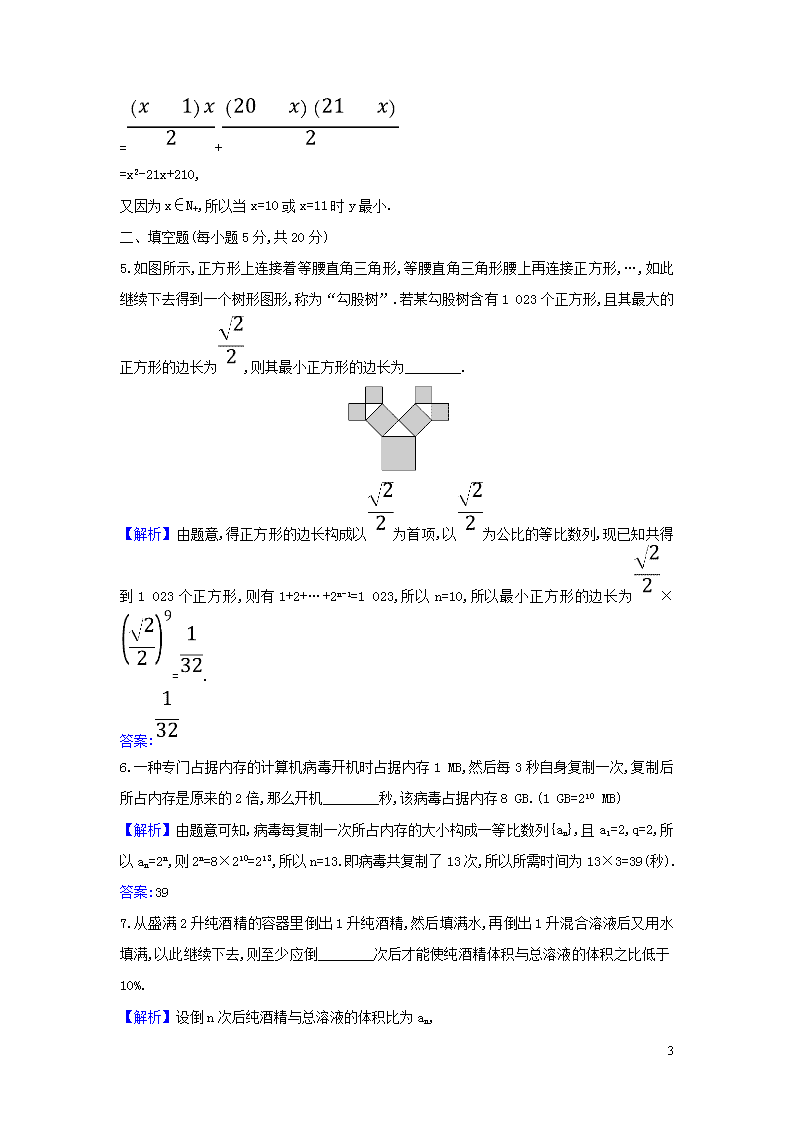D.‎ ‎【解析】选C.由题意知所得新数列为1×,×,×,…,×,所以a1a2+a2a3+a3a4+…+an-1an=+++…+‎ ‎=+++…+-==.‎ ‎4.(多选)植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边.现将树坑从1到20依次编号,为使各位同学从各自树坑前来领取树苗所走的路程总和最小,树苗可以放置的两个最佳坑位的编号为 (　　)‎ A.9 B.10 C.11 D.12‎ ‎【解析】选BC.设在x个坑处最佳,则x∈N+且1≤x≤20,则所有同学路程为:‎ y=1+2+…+(x-1)+1+2+…+(20-x)‎ 5‎ ‎=+‎ ‎=x2-21x+210,‎ 又因为x∈N+,所以当x=10或x=11时y最小.‎ 二、填空题(每小题5分,共20分)‎ ‎5.如图所示,正方形上连接着等腰直角三角形,等腰直角三角形腰上再连接正方形,…,如此继续下去得到一个树形图形,称为“勾股树”.若某勾股树含有1 023个正方形,且其最大的正方形的边长为,则其最小正方形的边长为________. ‎ ‎【解析】由题意,得正方形的边长构成以为首项,以为公比的等比数列,现已知共得到1 023个正方形,则有1+2+…+2n-1=1 023,所以n=10,所以最小正方形的边长为×=.‎ 答案:‎ ‎6.一种专门占据内存的计算机病毒开机时占据内存1 MB,然后每3秒自身复制一次,复制后所占内存是原来的2倍,那么开机________秒,该病毒占据内存8 GB.(1 GB=210 MB) ‎ ‎【解析】由题意可知,病毒每复制一次所占内存的大小构成一等比数列{an},且a1=2,q=2,所以an=2n,则2n=8×210=213,所以n=13.即病毒共复制了13次,所以所需时间为13×3=39(秒).‎ 答案:39‎ ‎7.从盛满2升纯酒精的容器里倒出1升纯酒精,然后填满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒________次后才能使纯酒精体积与总溶液的体积之比低于10%. ‎ ‎【解析】设倒n次后纯酒精与总溶液的体积比为an,‎ 5‎ 则an=,由题意知<10%,所以n≥4.‎ 答案:4‎ ‎8.定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,ak中0的个数不少于1的个数.若m=4,则不同的“规范01数列”的个数为________.  ‎ ‎【解析】由题意可得a1=0,a8=1,a2,a3,…,a7中有3个0,3个1,且满足对任意 k≤8,都有a1,a2,…,ak中0的个数不少于1的个数,利用列举法可得不同的“规范01数列”有00 001 111,00 010 111,00 011 011,00 011 101,00 100 111,00 101 011,00 101 101,00 110 011,00 110 101,01 000 111,01 001 011,01 001 101,01 010 011,01 010 101,共14个.‎ 答案:14‎ 三、解答题(每小题10分,共20分)‎ ‎9.某企业的资金每一年都比上一年分红后的资金增加一倍,并且每年年底固定给股东们分红500万元.该企业2018年年底分红后的资金为1 000万元. ‎ ‎(1)求该企业2022年年底分红后的资金.‎ ‎(2)求该企业从哪一年开始年底分红后的资金超过32 500万元.‎ ‎【解析】设an为(2018+n)年年底分红后的资金,‎ 其中n∈N*,则a1=2×1 000-500=1 500,‎ a2=2×1 500-500=2 500,…,an=2an-1-500(n≥2).所以an-500=2(an-1-500)(n≥2),‎ 即数列{an-500}是首项为a1-500=1 000,公比为2的等比数列.所以an-500=1 000×2n-1,‎ 所以an=1 000×2n-1+500.‎ ‎(1)a4=1 000×24-1+500=8 500,所以该企业2022年年底分红后的资金为8 500万元.‎ ‎(2)由an>32 500,即2n-1>32,得n>6,所以该企业从2025年开始年底分红后的资金超过32 500万元.‎ ‎10.科学研究证实,二氧化碳等温室气体的排放(简称碳排放)对全球气候和生态环境产生了负面影响,环境部门对A市每年的碳排放总量规定不能超过550万吨,否则将采取紧急限排措施.已知A市2018年的碳排放总量为400万吨,通过技术改造和倡导低碳生活等措施,此后每年的碳排放量比上一年的碳排放总量减少10%.同时,因经济发展和人口增加等因素,每年又新增加碳排放量m万吨(m>0).‎ 5‎ ‎(1)求A市2020年的碳排放总量(用含m的式子表示).‎ ‎(2)若A市永远不需要采取紧急限排措施,求m的取值范围.‎ ‎【解析】设2019年的碳排放总量为a1,2020年的碳排放总量为a2,‎ ‎(1)由已知a1=400×0.9+m,‎ a2=0.9×(400×0.9+m)+m=400×0.92+0.9m+m=324+1.9m.‎ ‎(2)a3=0.9×(400×0.92+0.9m+m)+m ‎=400×0.93+0.92m+0.9m+m,…,‎ an=400×0.9n+0.9n-1m+0.9n-2m+…+0.9m+m ‎=400×0.9n+m ‎=400×0.9n+10m(1-0.9n)‎ ‎=(400-10m)·0.9n+10m.‎ 由已知有∀n∈N*,an≤550,‎ 当400-10m=0即m=40时,显然满足题意;‎ 当400-10m>0即m<40时,由指数函数的性质可得:(400-10m)×0.9+10m≤550,解得m≤190.‎ 综合得m<40;‎ 当400-10m<0即m>40时,由指数函数的性质可得10m≤550,解得m≤55,综合得40