2018届二轮复习5-1平面向量的概念及线性运算课件（全国通用） 32页

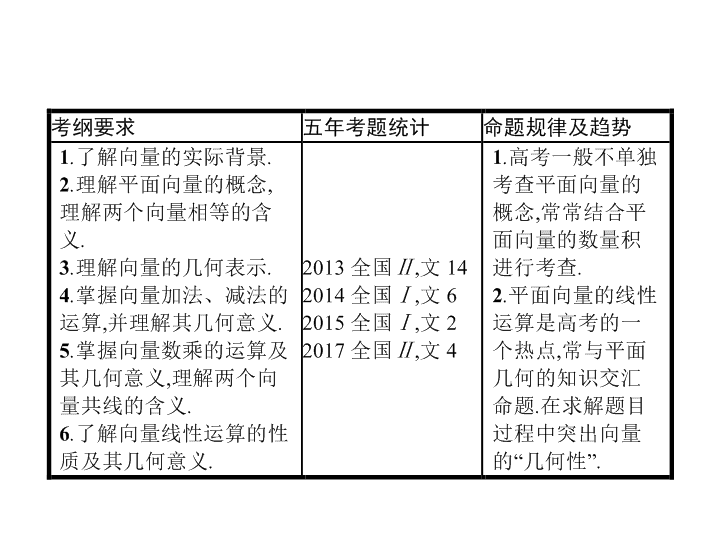
5 . 1 　 平面向量的概念及线性运算 - 2 - - 3 - 知识梳理 考点自测 1 . 向量的有关概念 大小 方向 长度 模 0 1 个单位 相同 　 相反 方向相同或相反 平行 - 4 - 知识梳理 考点自测 相等 相同 相等 相反 - 5 - 知识梳理 考点自测 2 . 向量的线性运算 b + a a + ( b + c ) - 6 - 知识梳理 考点自测 | λ || a | 相同 相反 λμ a λ a + μ a λ a + λ b - 7 - 知识梳理 考点自测 3 . 向量共线定理 (1) 向量 b 与 a ( a ≠ 0 ) 共线 , 当且仅当有唯一一个实数 λ , 使得 　　　　 . 注 : 限定 a ≠ 0 的目的是保证实数 λ 的存在性和唯一性 . (2) 变形形式 : 已知直线 l 上三点 A , B , P , O 为直线 l 外任一点 , 有且只有一个实数 λ , 使得 b = λ a - 8 - 知识梳理 考点自测 3 . 首尾顺次相接的多个向量的和等于从第一个向量的起点指向最后一个向量的终点的向量 , 一个封闭图形首尾连接而成的向量和为零向量 . - 9 - 知识梳理 考点自测 × √ × × × - 10 - 知识梳理 考点自测 2 . (2017 全国 Ⅱ , 文 4) 设非零向量 a , b 满足 | a + b |=| a - b | , 则 ( 　　 ) A . a ⊥ b B .| a |=| b | C . a ∥ b D .| a |>| b | 3 . 已知 , 且四边形 ABCD 为平行四边形 , 则 ( 　　 ) A. a-b+c-d=0 B. a-b+c+d=0 C. a+b-c-d=0 D. a+b+c+d=0 A 解析 : 由 | a + b |=| a - b | , 平方得 a 2 + 2 a · b + b 2 = a 2 - 2 a · b + b 2 , 即 a · b = 0 . 又 a , b 为非零向量 , 故 a ⊥ b , 故选 A . A - 11 - 知识梳理 考点自测 4 . (2017 北京海淀一模 , 文 6) 在 △ ABC 中 , 点 D 满足 则 ( 　　 ) A. 点 D 不在直线 BC 上 B. 点 D 在 BC 的延长线上 C. 点 D 在线段 BC 上 D. 点 D 在 CB 的延长线上 D - 12 - 知识梳理 考点自测 5 . 设向量 a , b 不平行 , 向量 λ a + b 与 a + 2 b 平行 , 则实数 λ = 　　　　　 . - 13 - 考点一 考点二 考点三 学科素养微专题 平面向量的有关概念 例 1 (1) 对于非零向量 a , b ,“ a + b = 0 ” 是 “ a ∥ b ” 的 ( 　　 ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 (2) 给出下列命题 : ① 若 |a|=|b| , 则 a=b 或 a=-b ; ② 若 A , B , C , D 是不共线的四点 , 则 “ ” 是 “ 四边形 ABCD 为平行四边形 ” 的充要条件 ; ③ 若两个向量相等 , 则它们的起点相同 , 终点相同 ; ④ a=b 的充要条件是 |a|=|b| , 且 a ∥ b . 其中真命题的序号是 　　　　　 . A ② - 14 - 考点一 考点二 考点三 学科素养微专题 解析 : (1) 若 a+b=0 , 则 a=-b , 所以 a ∥ b. 若 a ∥ b , 则 a+b=0 不一定成立 , 故前者是后者的充分不必要条件 . (2) ① 不正确 . 两个向量的长度相等 , 方向可以是任意的 ; 又 A , B , C , D 是不共线的四点 , ∴ 四边形 ABCD 为平行四边形 . 反之 , 若四边形 ABCD 为平行四边形 , ③ 不正确 . 相等向量的起点和终点可以都不同 ; ④ 不正确 . 当 a ∥ b 且方向相反时 , 即使 |a|=|b| , 也不能得到 a=b . 综上所述 , 真命题的序号是 ② . - 15 - 考点一 考点二 考点三 学科素养微专题 思考 学习了向量的概念后 , 你对向量有怎样的认识 ? 解题心得 对于向量的概念应注意以下几条 : (1) 向量的两个特征 : 大小和方向 . 向量既可以用有向线段和字母表示 , 也可以用坐标表示 . (2) 相等向量不仅模相等 , 而且方向要相同 , 所以相等向量一定是平行向量 , 而平行向量未必是相等向量 . (3) 向量与数量不同 , 数量可以比较大小 , 向量则不能 , 所以向量只有相等与不相等 , 不可以比较大小 . - 16 - 考点一 考点二 考点三 学科素养微专题 对点训练 1 (1) 给出下列命题 : ① 两个具有公共终点的向量一定是共线向量 ; ② 两个向量不能比较大小 , 但它们的模能比较大小 ; ③ 若 λ a = 0 ( λ 为实数 ), 则 λ 必为零 ; ④ 已知 λ , μ 为实数 , 若 λ a = μ b , 则 a 与 b 共线 . 其中错误命题的个数为 ( 　　 ) A.1 B.2 C.3 D.4 (2) 设 a 0 为单位向量 , ① 若 a 为平面内的某个向量 , 则 a=|a|a 0 ; ② 若 a 与 a 0 平行 , 则 a=|a|a 0 ; ③ 若 a 与 a 0 平行 , 且 |a|= 1, 则 a=a 0 . 上述命题中 , 假命题的个数为 　　　　　 .  C 3 - 17 - 考点一 考点二 考点三 学科素养微专题 解析 : (1) ① 错误 . 当方向不同时 , 不是共线向量 ; ② 正确 . 因为向量有方向 , 所以它们不能比较大小 , 但它们的模均为实数 , 故可以比较大小 ; ③ 错误 . 当 a = 0 时 , 不论 λ 为何值 , λ a = 0 ; ④ 错误 . 当 λ = μ = 0 时 , λ a = μ b , 此时 , a 与 b 可以是任意向量 . (2) 向量是既有大小又有方向的量 , a 与 |a|a 0 的模相等 , 但方向不一定相同 , 故 ① 是假命题 ; 若 a 与 a 0 平行 , 则 a 与 a 0 的方向有两种情况 : 一是同向 , 二是反向 , 反向时 a=-|a|a 0 , 故 ②③ 也是假命题 . 综上所述 , 假命题的个数是 3 . - 18 - 考点一 考点二 考点三 学科素养微专题 平面向量的线性运算 B A - 19 - 考点一 考点二 考点三 学科素养微专题 - 20 - 考点一 考点二 考点三 学科素养微专题 思考 在几何图形中 , 用已知向量表示未知向量的一般思路是什么 ? 向量的线性运算与代数多项式的运算有怎样的联系 ? 解题心得 1 . 进行向量运算时 , 要尽可能地将它们转化到三角形或平行四边形中 , 充分利用相等向量、相反向量、三角形的中位线及相似三角形的对应边成比例等性质 , 把未知向量用已知向量表示出来 . 2 . 向量的线性运算类似于代数多项式的运算 , 实数运算中的去括号、移项、合并同类项、提取公因式等变形手段在向量的线性运算中同样适用 . - 21 - 考点一 考点二 考点三 学科素养微专题 A - 22 - 考点一 考点二 考点三 学科素养微专题 - 23 - 考点一 考点二 考点三 学科素养微专题 向量共线定理及其应用 例 3 设两个非零向量 a 与 b 不共线 . - 24 - 考点一 考点二 考点三 学科素养微专题 - 25 - 考点一 考点二 考点三 学科素养微专题 思考 如何用向量的方法证明三点共线 ? 解题心得 1 . 证明三点共线问题 , 可用向量共线解决 , 但应注意向量共线与三点共线的区别与联系 , 当两向量共线且有公共点时 , 才能得出三点共线 . 2 . 向量 a , b 共线是指存在不全为零的实数 λ 1 , λ 2 , 使 λ 1 a + λ 2 b = 0 成立 ; 若 λ 1 a + λ 2 b = 0 当且仅当 λ 1 = λ 2 = 0 时成立 , 则向量 a , b 不共线 . - 26 - 考点一 考点二 考点三 学科素养微专题 D D - 27 - 考点一 考点二 考点三 学科素养微专题 - 28 - 考点一 考点二 考点三 学科素养微专题 1 . 平面向量的重要结论 : (1) 若存在非零实数 λ , 使得 , 则 A , B , C 三点共线 . (2) 相等向量具有传递性 , 非零向量的平行具有传递性 . (3) 向量可以平移 , 平移后的向量与原向量是相等向量 . 2 . a 与 b 共线 ⇔ b = λ a ( a ≠ 0 , λ 为实数 ) . 3 . 向量的线性运算要满足三角形法则和平行四边形法则 , 做题时 , 要注意三角形法则与平行四边形法则的要素 . 向量加法的三角形法则要素是 “ 首尾相接 , 指向终点 ”; 向量减法的三角形法则要素是 “ 起点重合 , 指向被减向量的终点 ”; 平行四边形法则要素是 “ 起点重合 ” . - 29 - 考点一 考点二 考点三 学科素养微专题 1 . 若两个向量起点相同 , 终点相同 , 则这两个向量相等 ; 但两个相等向量不一定有相同的起点和终点 . 2 . 零向量和单位向量是两个特殊的向量 . 它们的模确定 , 但方向不确定 . 3 . 注意区分向量共线与向量所在的直线平行之间的关系 . 向量 是共线向量 , 但 A , B , C , D 四点不一定在同一条直线上 . 4 . 在向量共线的充要条件中要注意 “ a ≠ 0 ”, 否则 λ 可能不存在 , 也可能有无数个 . - 30 - 考点一 考点二 考点三 学科素养微专题 典例 (1) 下列命题正确的是 　　　　　 . ( 填序号 )   ① 向量 a , b 共线的充要条件是有且仅有一个实数 λ , 使 b = λ a ; ② 在 △ ABC 中 , ③ 不等式 || a |-| b || ≤ | a + b | ≤ | a |+| b | 中两个等号不可能同时成立 ; ④ 只有方向相同或相反的向量是平行向量 ; ⑤ 若向量 a , b 不共线 , 则向量 a+b 与向量 a - b 必不共线 . (2) 下列叙述错误的是 　　　　　　　　 .   ① 若非零向量 a 与 b 的方向相同或相反 , 则 a+b 与 a , b 其中之一的方向相同 ; ② |a|+|b|=|a+b| ⇔ a 与 b 的方向相同 ; ④ 若 λ a = λ b , 则 a = b . 易错警示 —— 都是零向量 “ 惹的祸 ” ⑤ ①②③④ - 31 - 考点一 考点二 考点三 学科素养微专题 解析 : (1) 易知 ①②③④ 错误 . - 32 - 考点一 考点二 考点三 学科素养微专题 反思提升 在向量的有关概念中 , 定义长度为 0 的向量叫做零向量 , 其方向是任意的 , 并且规定 : 0 与任一向量平行 . 由于零向量的特殊性 , 在两个向量共线或平行问题上 , 如果不考虑零向量 , 那么往往会得到错误的判断或结论 . 在向量的运算中 , 很多学生也往往忽视 0 与 0 的区别 , 导致结论错误 .