2021届课标版高考文科数学一轮复习教师用书：第七章第二讲　二元一次不等式（组）与简单的线性规划问题 9页

第二讲　二元一次不等式(组)与简单的线性规划问题 ‎　　　　　　　　　　　　　　　　　　　 ‎ ‎1.[改编题]给出下列命题,其中真命题的个数为(　　)‎ ‎①原点能判断二元一次不等式Ax+By+C>0所表示的平面区域在直线Ax+By+C=0的哪一侧;‎ ‎②不等式Ax+By+C>0表示的平面区域一定在直线Ax+By+C=0的上方;‎ ‎③点(x1,y1),(x2,y2)在直线Ax+By+C=0同侧的充要条件是(Ax1+By1+C)(Ax2+By2+C)>0,异侧的充要条件是(Ax1+By1+C)(Ax2+By2+C)<0.‎ ‎　　　　　　　　　　　　　　　　　　‎ A.0 B.1 C.2 D.3‎ ‎2.[2019北京,5,5分]若x,y满足|x|≤1 - y,且y≥ - 1,则3x+y的最大值为(　　)‎ A. - 7 B.1 C.5 D.7‎ ‎3.[2019浙江,3,4分]若实数x,y满足约束条件x - 3y+4≥0,‎‎3x - y - 4≤0,‎x+y≥0,‎则z=3x+2y的最大值是(　　)‎ A. - 1 B.1 C.10 D.12‎ ‎4.[2015福建,10,5分][文]变量x,y满足约束条件x+y≥0,‎x - 2y+2≥0,‎mx - y≤0.‎若z=2x - y的最大值为2,则实数m等于(　　)‎ A. - 2 B. - 1 C.1 D.2‎ ‎5.[2020广东七校联考]若x,y满足约束条件x≥ - 2,‎x+y≥0,‎x - y+2≤0,‎则z=x - 2y的最大值为　　　　. ‎ ‎6.[2015新课标全国Ⅰ,15,5分]若x,y满足约束条件x - 1≥0,‎x - y≤0,‎x+y - 4≤0,‎则yx的最大值为　　　　. ‎ 考法1 平面区域问题　　　　　　　　　　　　　　‎ ‎1[2015重庆,10,5分][文]若不等式组x+y - 2≤0,‎x+2y - 2≥0,‎x - y+2m≥0‎表示的平面区域为三角形及其内部,且其面积等于‎4‎‎3‎,则m的值为 ‎　　　　　　　　　　　　　　　　　　　‎ A. - 3 B.1 C.‎4‎‎3‎ D.3‎ 先正确作出不含参数m的不等式构成的二元一次不等式组所表示的平面区域,然后通过平移直线x - y=0来观察原不等式组所围成平面区域的形状是否为三角形,从而得出参数m的取值范围,最后根据不等式组表示的平面区域的面积求出参数m的值.‎ 作出不等式组表示的平面区域,如图7 - 2 - 1中阴影部分(包含边界)所示,由图可知,要使不等式组表示的平面区域的形状为三角形,则m> - 1.由x+y - 2=0,‎x - y+2m=0,‎解得x=1 - m,‎y=1+m,‎即A(1 - m,1+m).由x+2y - 2=0,‎x - y+2m=0,‎解得x=‎2‎‎3‎ - ‎4‎‎3‎m,‎y=‎2‎‎3‎+‎2‎‎3‎m,‎即B(‎2‎‎3‎‎--‎‎4‎‎3‎m,‎2‎‎3‎‎+‎‎2‎‎3‎m).易知直线x - y+2m=0与x轴交于点D( - 2m,0). ‎ 因为S△ABC=S△ADC - S△BDC=‎1‎‎2‎(2+2m)[1+m - (‎2‎‎3‎‎+‎‎2‎‎3‎m)]=‎1‎‎3‎(m+1)2=‎4‎‎3‎,所以m=1.‎ B 易错警示 在画二元一次不等式(组)表示的平面区域时,要注意以下两个问题:(1)边界线是虚线还是实线;(2)选取的平面区域在直线的哪一侧.‎ ‎1.不等式组‎2x+y - 6≤0,‎x+y - 3≥0,‎y≤2‎表示的平面区域的面积为(　　)‎ A.4 B.1 ‎ C.5 D.无穷大 考法2 求目标函数的最值(范围)　　　　　　　　　　　　　　　　　‎ 命题角度1　求线性目标函数的最值 ‎2[2020成都市高三摸底测试]若实数x,y满足约束条件x+2y - 2≤0,‎x - 1≥0,‎y≥0,‎则z=x - 2y的最小值为 A.0 B.2 C.4 D.6‎ 思路一　先画出不等式组表示的平面区域,然后平移直线x - 2y=0,再根据目标函数的几何意义确定出其最小值.‎ 思路二　先求出可行域各顶点的坐标,然后分别计算出各顶点处的目标函数值,再找出最小值.‎ 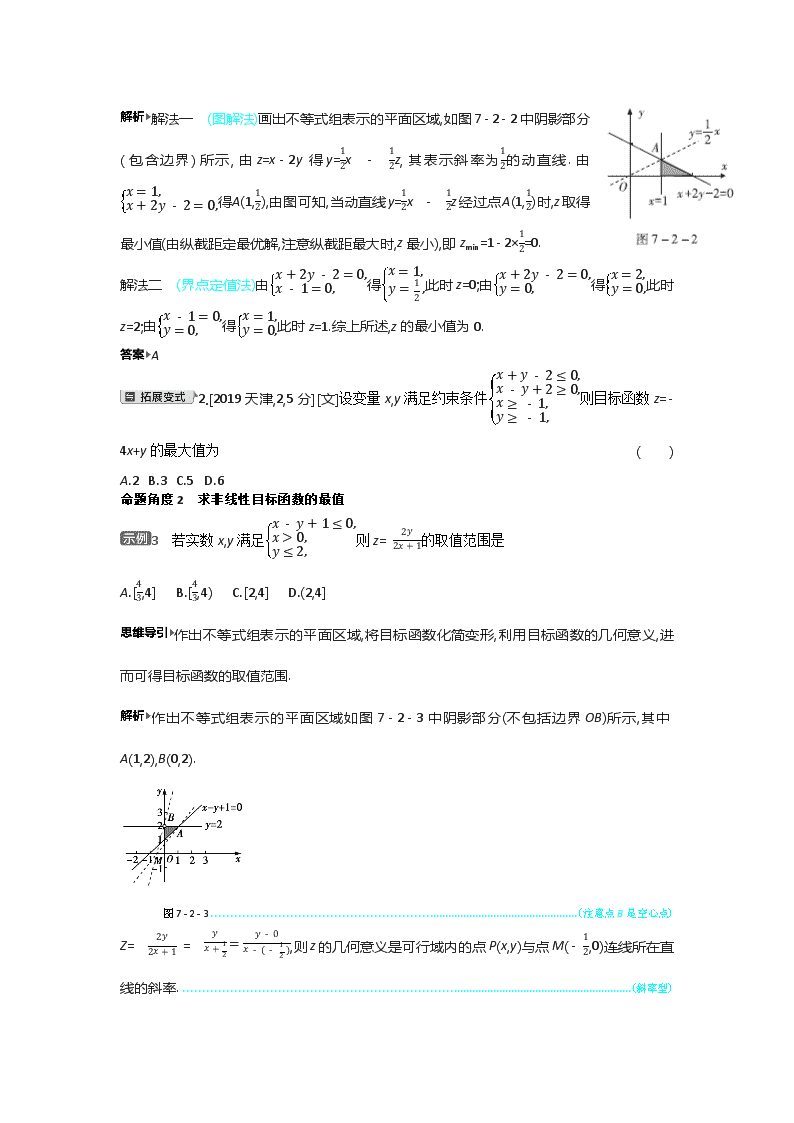解法一　(图解法)画出不等式组表示的平面区域,如图7 - 2 - 2中阴影部分(包含边界)所示,由z=x - 2y得y=‎1‎‎2‎x - ‎1‎‎2‎z,其表示斜率为‎1‎‎2‎的动直线.由x=1,‎x+2y - 2=0,‎得A(1,‎1‎‎2‎),由图可知,当动直线y=‎1‎‎2‎x - ‎1‎‎2‎z经过点A(1,‎1‎‎2‎)时,z取得最小值(由纵截距定最优解,注意纵截距最大时,z最小),即zmin=1 - 2×‎1‎‎2‎=0. ‎ 解法二　(界点定值法)由x+2y - 2=0,‎x - 1=0,‎得x=1,‎y=‎1‎‎2‎,‎此时z=0;由x+2y - 2=0,‎y=0,‎ 得x=2,‎y=0,‎此时z=2;由x - 1=0,‎y=0,‎得x=1,‎y=0,‎此时z=1.综上所述,z的最小值为0.‎ A ‎2.[2019天津,2,5分][文]设变量x,y满足约束条件x+y - 2≤0,‎x - y+2≥0,‎x≥ - 1,‎y≥ - 1,‎则目标函数z= - 4x+y的最大值为(　　)‎ A.2 B.3 C.5 D.6‎ 命题角度2　求非线性目标函数的最值 ‎3 若实数x,y满足x - y+1≤0,‎x>0,‎y≤2,‎则z= ‎2y‎2x+1‎的取值范围是 A.[‎4‎‎3‎,4] B.[‎4‎‎3‎,4) C.[2,4] D.(2,4]‎ 作出不等式组表示的平面区域,将目标函数化简变形,利用目标函数的几何意义,进而可得目标函数的取值范围.‎ 作出不等式组表示的平面区域如图7 - 2 - 3中阴影部分(不包括边界OB)所示,其中A(1,2),B(0,2).‎ 图7 - 2 - 3(注意点B是空心点)‎ Z= ‎2y‎2x+1‎ = yx+‎‎1‎‎2‎‎=‎y - 0‎x - ( - ‎1‎‎2‎)‎,则z的几何意义是可行域内的点P(x,y)与点M( - ‎1‎‎2‎,0)连线所在直线的斜率.(斜率型)‎ 可知kMA=‎2 - 0‎‎1 - ( - ‎1‎‎2‎)‎‎=‎‎4‎‎3‎,kMB=‎2 - 0‎‎0 - ( - ‎1‎‎2‎)‎=4,结合图形可得‎4‎‎3‎≤z<4. ‎ 故z=‎2y‎2x+1‎的取值范围是[‎4‎‎3‎,4).‎ B ‎3.设x,y满足约束条件x - y+5≥0,‎x+y≥0,‎x≤3,‎则z=(x+1)2+y2的最大值为(　　)‎ A.80 B.4‎5‎ C.25 D.‎‎17‎‎2‎ 考法3 含参线性规划问题　　　　　　　　　　　　　　　　　‎ ‎4已知z=2x+y,其中实数x,y满足y≥x,‎x+y≤2,‎x≥a,‎且z的最大值是最小值的4倍,则a的值是 ‎　　　　　　　　　　　　　　　　　　　‎ A.‎2‎‎11‎ B.‎1‎‎4‎ C.4 D.‎‎11‎‎2‎ 作出不等式组表示的平面区域,利用z的几何意义,结合z的最大值是最小值的4倍建立方程,即可得出结果.‎ 作出不等式组表示的平面区域如图7 - 2 - 4中阴影部分(包括边界)所示. (把参数当成常数)‎ 由z=2x+y,得y= - 2x+z.‎ 由图象可知,当直线y= - 2x+z经过点A时,直线在y轴上的截距最大,此时z最大.‎ 由x+y=2,‎y=x,‎解得x=1,‎y=1,‎即A(1,1),故zmax=2×1+1=3,‎ 当直线y= - 2x+z经过点B时,直线在y轴上的截距最小,此时z最小. ‎ 由x=a,‎y=x,‎解得x=a,‎y=a,‎即B(a,a),故zmin=2×a+a=3a. (求线性目标函数的最值)‎ 由z的最大值是最小值的4倍,得3=4×3a,即a=‎1‎‎4‎. (构造方程求参数)‎ B ‎4.若实数x,y满足不等式组x - y+2≥0,‎x+2y - 4≥0,‎‎2x+y - 5≤0,‎且3(x - a)+2(y+1)的最大值为5,则a=　　　　. ‎ 考法4 线性规划的实际应用　　　　　　　　　　　　　　　　　‎ ‎5 某共享汽车品牌在某市投放1 500辆宝马轿车,为人们的出行提供了一种新的交通方式.该市的市民小王喜欢自驾游,他在该市通过网络组织了一场“周日租车游”活动,招募了30名自驾游爱好者租车旅游,他们计划租用A,B两种型号的宝马轿车,已知A,B两种型号的宝马轿车每辆的载客量都是5人,每天的租金分别为600元/辆和1 000元/辆,要求租车总数不超过12辆且不少于6辆,并且A,B两种型号的宝马轿车至少各租用1辆,则租车所需的租金最少为　　　　　元. ‎ 先确定变量,然后根据已知条件列出变量所满足的不等式组以及目标函数,进而根据目标函数的几何意义确定最优解,求得目标函数的最值,最后还原为实际问题即可.‎ 设分别租用A,B两种型号的宝马轿车x辆、y辆,所需的总租金为z元,则z=600x+1 000y,其中x,y满足不等式组‎5x+5y≥30,‎‎6≤x+y≤12,‎x≥1,‎y≥1,‎x,y‎∈N‎*‎,‎作出不等式组 x+y≥6,‎x+y≤12,‎x≥1,‎y≥1‎所表示的平面区域如图7 - 2 - 5中阴影部分(包含边界)所示, ‎ 目标函数可化为y= - ‎3‎‎5‎x+z‎1 000‎,由图可知当直线y= - ‎3‎‎5‎x+z‎1 000‎过点C时,目标函数z取得最小值.由x+y=6,‎y=1,‎解得C(5,1).所以总租金z的最小值为600×5+‎ ‎1 000×1=4 000(元).‎ ‎5.[2016全国卷Ⅰ,16,5分][文]某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为　　　　元. ‎ ‎301‎ ‎1.B　①当原点在直线Ax+By+C=0上时,无法判断Ax+By+C>0所表示的平面区域在直线Ax+By+C=0的哪一侧,故①错误;②x - y+1>0表示的平面区域是直线x - y+1=0下方的区域,故②错误;③将直线同一侧的所有点的坐标代入Ax+By+C,所得到的实数的符号相同,将异侧的所有点的坐标代入Ax+By+C,所得到的实数的符号相反,故③正确.选B.‎ ‎2.C　令z=3x+y,画出不等式组‎|x|≤1 - y,‎y≥ - 1,‎即不等式组x≤1 - y,‎x≥0,‎y≥ - 1‎或‎ - x≤1 - y,‎x<0,‎y≥ - 1‎ 表示的平面区域,如图D 7 - 2 - 1中阴影部分(包含边界)所示,作出直线y= - 3x并平移,由数形结合可知,当平移后的直线过点C(2, - 1)时,z=3x+y取得最大值,zmax=3×2 - 1=5.故选C.‎ 图D 7 - 2 - 1‎ ‎3.C　作出可行域如图D 7 - 2 - 2中阴影部分(包含边界)所示,由数形结合可知,当直线z=3x+2y过点A(2,2)时,z取得最大值,zmax=6+4=10.故选C.‎ 图D 7 - 2 - 2‎ ‎4.C　画出x+y≥0,‎x - 2y+2≥0‎表示的区域,如图D 7 - 2 - 3阴影部分所示,mx - y=0过定点(0,0),当m≤‎1‎‎2‎时,z=2x - y无最大值,当m>‎1‎‎2‎时,x+y≥0,‎x - 2y+2≥0,‎mx - y≤0‎表示区域为图中△OAB及其内部,则z=2x - y过点A时取得最大值2,由mx - y=0,‎x - 2y+2=0,‎得A(‎2‎‎2m - 1‎,‎2m‎2m - 1‎),则2×‎2‎‎2m - 1‎‎ - ‎‎2m‎2m - 1‎=2,解得m=1,故选C.‎ 图D 7 - 2 - 3‎ ‎5. - 3　作出可行域,如图D 7 - 2 - 4中阴影部分所示,由z=x - 2y,可得y=‎1‎‎2‎x - ‎1‎‎2‎z,其表示斜率为‎1‎‎2‎,纵截距为 - ‎1‎‎2‎z的直线,作出直线y=‎1‎‎2‎x并平移,当平移后的直线过点A( - 1,1)时,直线在y轴上的截距最小,此时z取得最大值,zmax= - 1 - 2×1= - 3.‎ 图D 7 - 2 - 4‎ ‎6.3　作出可行域如图D 7 - 2 - 5中阴影部分所示,易知在点A(1,3)处,yx取得最大值3. ‎ 图D 7 - 2 - 5‎ ‎1.B　不等式组‎2x+y - 6≤0,‎x+y - 3≥0,‎y≤2‎表示的平面区域如图D 7 - 2 - 6中阴影部分(包含边界)所示,△ABC的面积即为所求.由图求得点A,B,C的坐标分别为A(1,2),B(2,2),C(3,0),则△ABC的面积为S=‎1‎‎2‎×(2 - 1)×2=1.故选B.‎ 图D 7 - 2 - 6‎ ‎2.C　画出可行域,如图D 7 - 2 - 7中阴影部分(包含边界)所示,‎ 图D 7 - 2 - 7‎ 作出直线 - 4x+y=0并平移,可知当直线z= - 4x+y过点A时,z取得最大值.由x= - 1,‎x - y+2=0‎可得x= - 1,‎y=1,‎所以点A的坐标为( - 1,1),‎ 故zmax= - 4×( - 1)+1=5.故选C.‎ ‎3.A　作出不等式组x - y+5≥0,‎x+y≥0,‎x≤3‎表示的平面区域,如图D 7 - 2 - 8中阴影部分(包含边界)所示.‎ 图D 7 - 2 - 8‎ ‎(x+1)2+y2表示可行域内的点(x,y)到点P( - 1,0)的距离的平方,由图可知可行域内的点A到点P( - 1,0)的距离最大.‎ 解方程组x=3,‎x - y+5=0,‎得x=3,‎y=8,‎即点A的坐标为(3,8),代入z=(x+1)2+y2,得zmax=(3+1)2+82=80.故选A.‎ ‎4.2　设z=3(x - a)+2(y+1),作出不等式组表示的平面区域如图 D 7 - 2 - 9中阴影部分(包含边界)所示.‎ D 7 - 2 - 9‎ 由z=3(x - a)+2(y+1),得y= - ‎3‎‎2‎x+‎3a - 2+z‎2‎,作出直线y= - ‎3‎‎2‎x,平移该直线,易知当直线z=3(x - a)+2(y+1)过点A(1,3)时,z取得最大值,‎ 又目标函数的最大值为5,所以3(1 - a)+2×(3+1)=5,解得a=2.‎ ‎5.216 000　由题意,设生产x件产品A,生产y件产品B,利润z=2 100x+900y,‎ 作出不等式组‎1.5x+0.5y≤150,‎x+0.3y≤90,‎‎5x+3y≤600,‎x≥0,‎y≥0‎表示的平面区域,如图D 7 - 2 - 10中阴影部分(包含边界)所示,‎ 图D 7 - 2 - 10‎ 由x∈N,y∈N,可知取得最大值时的最优解为(60,100),所以zmax=2 100×60+900×100=216 000(元).‎