- 96.73 KB
- 2021-06-15 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
空间向量法解决几何体外接球问题的研究
摘要:在高中数学学习中,空间向量法的引入在解决空间几何体相关问题中起到至关重要的作用。空间向量法的出现使几何体求解问题更加方便快捷,如求二面角问题,直线与平面及平面与平面间的相互关系问题等。该文根据空间球的一些特性及推论,阐述了运用空间向量法解决几何体外接球问题的新方法。通过对球及立体几何的认识,并学会运用空间向量方法解决立体几何问题,从而达到数学思维的活跃。
关键词:高中数学、空间向量法、外心法向量、几何体外接球
一、了解重要推论
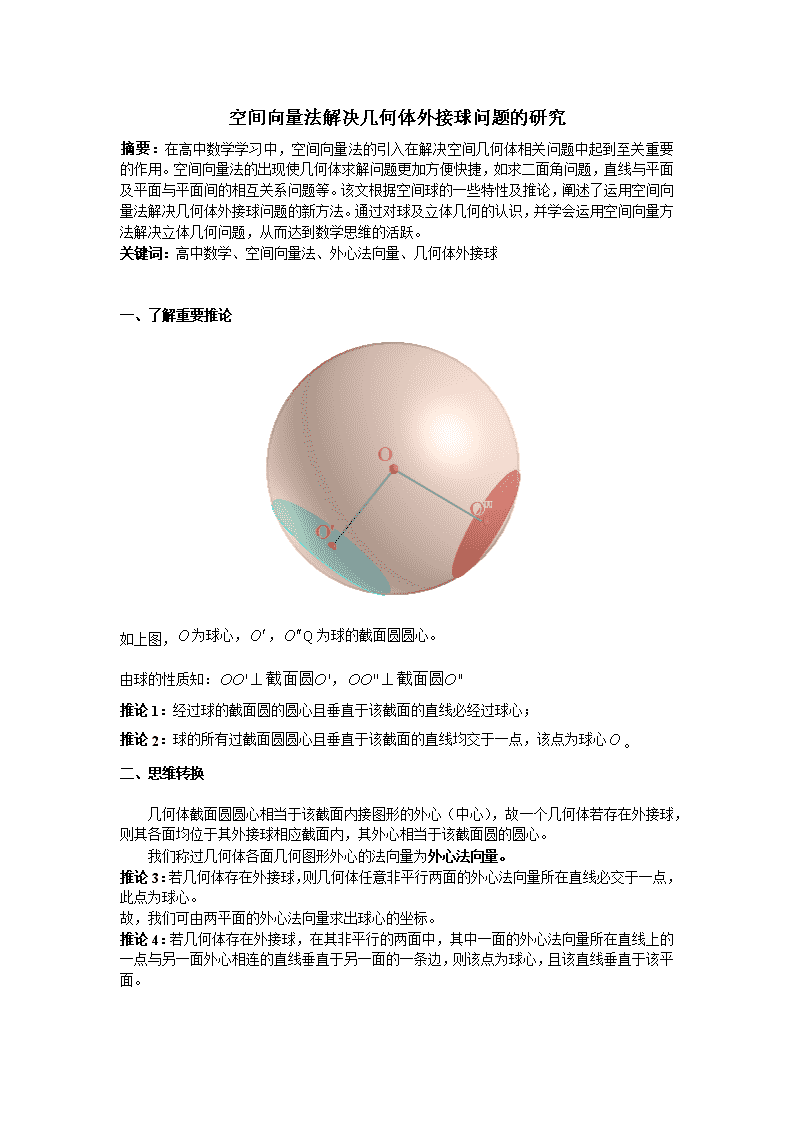
如上图,为球心,,Q为球的截面圆圆心。
由球的性质知:,
推论1:经过球的截面圆的圆心且垂直于该截面的直线必经过球心;
推论2:球的所有过截面圆圆心且垂直于该截面的直线均交于一点,该点为球心。
二、思维转换
几何体截面圆圆心相当于该截面内接图形的外心(中心),故一个几何体若存在外接球,则其各面均位于其外接球相应截面内,其外心相当于该截面圆的圆心。
我们称过几何体各面几何图形外心的法向量为外心法向量。
推论3:若几何体存在外接球,则几何体任意非平行两面的外心法向量所在直线必交于一点,此点为球心。
故,我们可由两平面的外心法向量求出球心的坐标。
推论4:若几何体存在外接球,在其非平行的两面中,其中一面的外心法向量所在直线上的一点与另一面外心相连的直线垂直于另一面的一条边,则该点为球心,且该直线垂直于该平面。
三、几何图形的外心坐标求解法
以平面直角坐标系为例:
其中,为的中点,各点坐标如图所示,故可求得
,
下面求外心H的坐标,设
则:
解得:,故外心坐标为。
注:
1.根据向量还可以求直线方程,如垂直平分线方程①和②;
2.在空间图形中求外心,应找出三条边的向量关系联立求出外心,因为空间中的旋转效应,单个关系求出的是平面。
四、空间向量法求几何体外接圆半径的步骤:
例:对于四面体,求外接圆半径的步骤:
①任取两面,求外心
如取面ABC和面BCS外心分别为
AB中点:
BC中点:
AC中点:
则有:
,联立求出,同理可求
②设球心坐标为,分别为两面外心法向量
联立求出,即球心坐标。
注:由推论4易知,④式可舍,不影响结果。
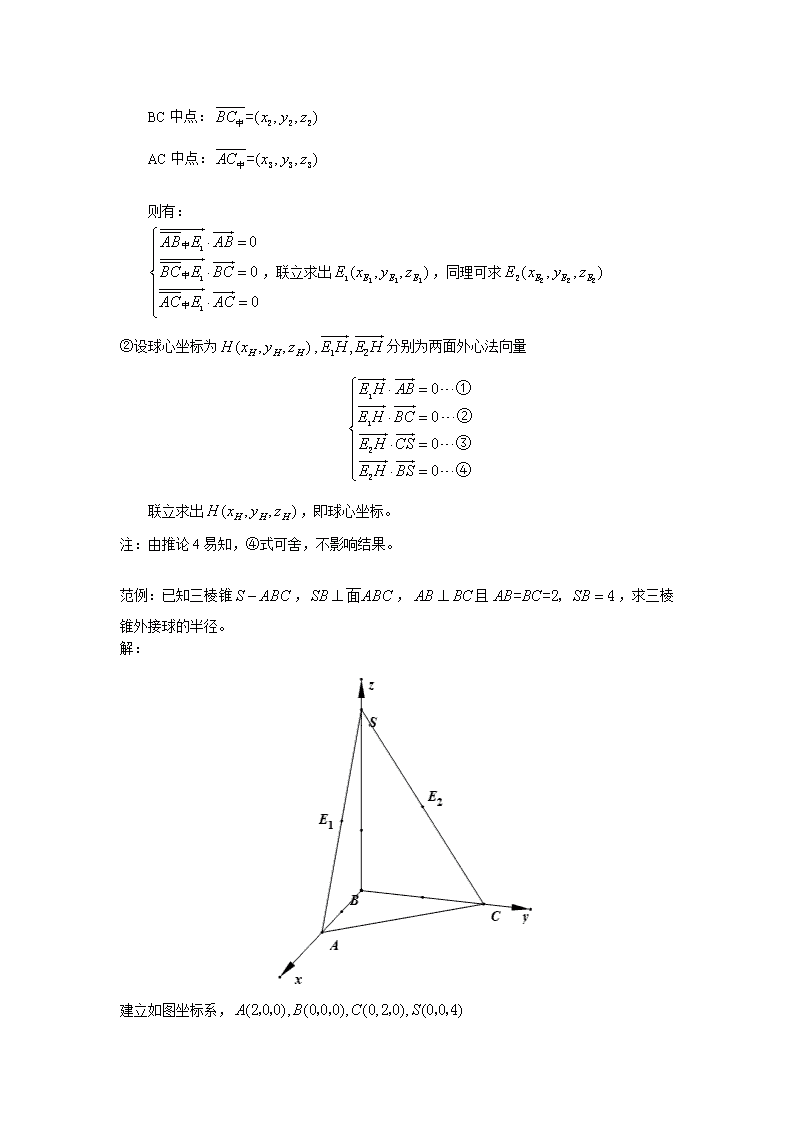
范例:已知三棱锥,,且,求三棱锥外接球的半径。
解:
建立如图坐标系,
面的外心,面的外心,设球心。
,,
联立,即
解得:
故球心坐标为
∴外接球半径
五、研究空间向量法解决几何体外接球问题的意义
数学是一门综合性比较强的学科,空间向量法的引入体现了数学交叉思想。本课题推导了空间向量法解决空间几何体外接球问题的方法,同时本文为空间向量法解决几何体内接球问题的方法做了铺垫(通过引入内心法向量解决)。