江西省赣州市石城中学2020届高三下学期第十次周考数学（理）试题 12页

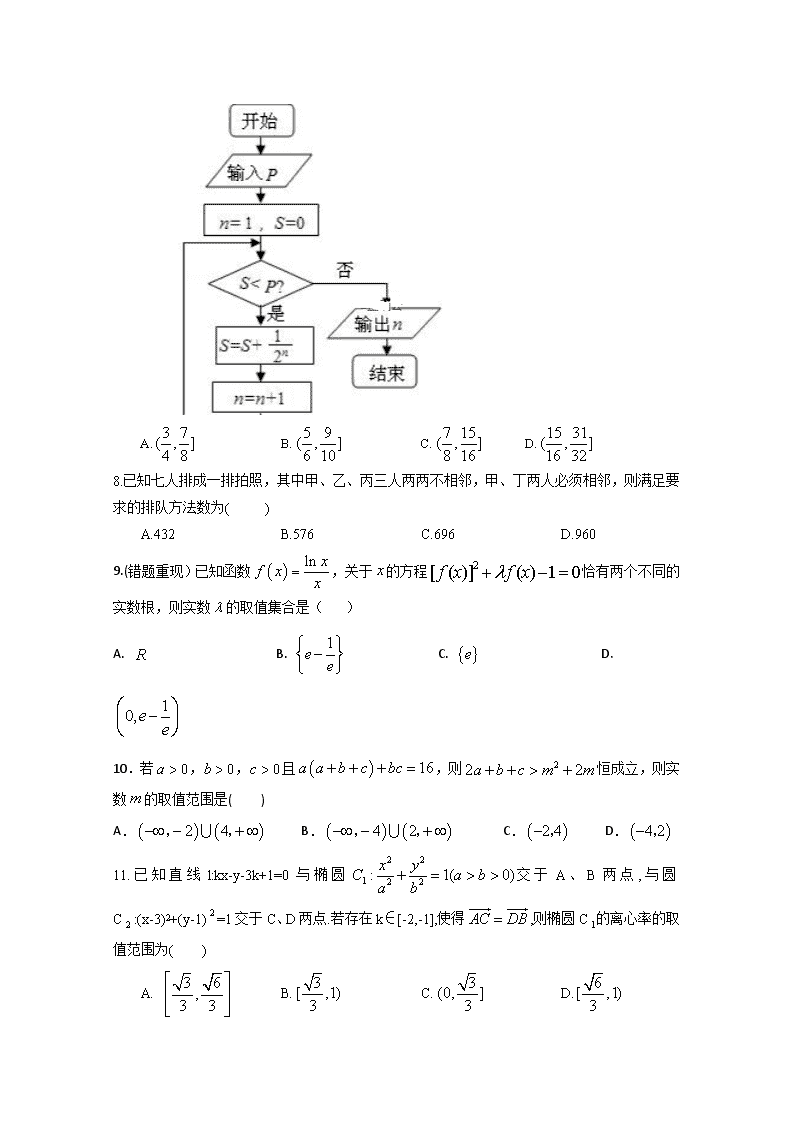
石城中学2020届高三下学期第十次周考 数学（理科）‎ 满分150分 时间120分钟 一、选择题：本大题共12个小题，每小题5分，共60分. ‎ ‎1.已知集合，集合，则（ ）‎ ‎ A. B. C. D. ‎ ‎2．在复平面内，复数z=i对应的点为Z，将向量绕原点O按逆时针方向旋转，所得向量对应的复数是（ ）‎ A. B. C. D. ‎ ‎3.在等比数列中，“是方程的两根”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎4.若，则（ ）‎ A B. C. D. ‎ ‎5.设F为抛物线的焦点，A, B,C为抛物线上三点,若则|( )‎ A.9 B.6 ‎ ‎6.函数（其中为自然对数的底数）的图象如图所示，则（ ）‎ A. ， B. ，‎ C. ， D. ，‎ ‎7.执行如图所示的程序框图后，输出的值为5,则P的取值范围是( )‎ A. B. C. D.‎ ‎8.已知七人排成一排拍照，其中甲、乙、丙三人两两不相邻，甲、丁两人必须相邻，则满足要求的排队方法数为( )‎ A.432 B‎.576 ‎ C.696 D.960‎ ‎9.(错题重现）已知函数，关于的方程恰有两个不同的实数根，则实数的取值集合是（ ）‎ A. B. C. D. ‎ ‎10．若且，则恒成立，则实数的取值范围是( )‎ A． B． C． D．‎ ‎11.已知直线l:kx-y-3k+1=0与椭圆交于A、B两点,与圆C:(x-3)2+(y-1)=1交于C、D两点.若存在k∈[-2,-1],使得,则椭圆C的离心率的取值范围为( )‎ A. B. C. D.‎ ‎12.数学中有许多形状优美、寓意美好的曲线,例如:四叶草曲线就是其中一种,其方程为(x+y)=xy.给出下列四个结论:‎ ‎①曲线C有四条对称轴;‎ ‎②曲线C上的点到原点的最大距离为;‎ ‎③曲线C第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为;‎ ‎④四叶草面积小于.‎ 其中,所有正确结论的序号是（ ）‎ A.①② B.①③ C.①③④ D.①②④‎ 二．填空题：（本大题共4小题，每小题5分，共20分）‎ ‎13．已知二项式的展开式中第2项与第3项的二项式系数之比是，则的系数为________．‎ ‎14.若为假，则实数a的取值范围为 .‎ ‎15.在直角坐标系xOy中，已知点A(0，1)和点B（-3，4），若点C在∠AOB的平分线上，且，则向量的坐标为 ‎ ‎16．已知抛物线C：y2=4x，点P为抛物线C上一动点，过点P作圆M：(x-3)2+y2=4的切 ‎ 线，切点分别为A，B，则线段AB长度的取值范围为 ‎ 三．解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎17.如图，等腰直角三角形中，，，点为内一点，且 ‎，.‎ ‎（1）求；‎ ‎（2）求.‎ ‎18.如图，四边形ABCD是菱形，平面ABCD，，平面BDE，G是AB中点．‎ 求证：平面BCF；‎ 若，，求二面角的余弦值．‎ ‎19．（本题满分12分）椭圆的左、右焦点分别为，，右顶点为A，上顶点为B，且满足向量．‎ ‎（1）若，求椭圆的标准方程；‎ ‎（2）设P为椭圆上异于顶点的点，以线段PB为直径的圆经过，问是否存在过的直线与该圆相切？若存在，求出其斜率；若不存在，说明理由．‎ ‎20.已知函数，曲线在点处的切线方程为.‎ ‎（1）求，的值；‎ ‎（2）证明函数存在唯一的极大值点，且.‎ ‎21.某工厂生产零件A，工人甲生产一件零件A，是一等品、二等品、三等品的概率分别为，工人乙生产一件零件A，是一等品、二等品、三等品的概率分别为．己知生产一件一等品、二等品、三等品零件A给工厂带来的效益分别为10元、5元、2元。‎ ‎ (I)试根据生产一件零件A给工厂带来的效益的期望值判断甲乙技术的好坏：‎ ‎ (II)为鼓励工人提高技术，工厂进行技术大赛，最后甲乙两人进入了决赛．决赛规则是：每一轮比赛，甲乙各生产一件零件A，如果一方生产的零件A品级优干另一方生产的零件，则该方得分1分，另一方得分-l分，如果两人生产的零件A品级一样，则两方都不得分，当一方总分为4分时，比赛结束，该方获胜．（i= -4，-3，-2，…4）表示甲总分为i时，最终甲获胜的概率．‎ ‎①写出的值；②求决赛甲获胜的概率．‎ ‎(二)选考题:共10分请考生在第22、23题中任选一题作答,如果多做,则技所做的第一题计分 ‎22.选修4-4:坐标系与参数方程 已知曲线C的极坐标方程是ρ＝2cos θ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是(t为参数)．‎ ‎(1)求曲线C的直角坐标方程和直线l的普通方程；‎ ‎(2)设点P(m,0)，若直线l与曲线C交于A，B两点，且|PA|·|PB|＝1，求实数m的值．‎ ‎23.[选修4-5：不等式选讲]‎ 已知函数.‎ ‎（1）解不等式：；‎ ‎（2）当时，函数的图象与轴围成一个三角形，求实数的取值范围.‎ 数学参考答案（理科）‎ 一、选择题：本大题共12个小题，每小题5分，共60分. ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B A A D C C C B B D A C 二、填空题（每题5分，共20分）‎ ‎13.240 14. 15.（-3，9） 16. ‎ 三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎17【详解】（1）由条件及两角和的正切公式得：‎ ‎，‎ 而，所以，‎ 则，‎ ‎∵，∴.‎ 在中，由正弦定理知：，即.‎ ‎（2）由（1）知，，而在等腰直角三角形中，，‎ ‎，所以，‎ 则.‎ 在中，由余弦定理，‎ ‎，‎ ‎∴，‎ ‎∵，∴.‎ ‎18.【详解】设，连结OE，OF，‎ 四边形ABCD是菱形，平面ABCD，，平面BDE，‎ ‎，，平面ABCD，‎ 设，，，‎ 以O为原点，OA，OB，OF所在直线分别为x，y，z轴，建立空间直角坐标系，‎ 则0，，，b，，0，，0，，‎ b，，0，，，‎ 设平面BCF的法向量为y，，‎ 则，取，得c，，‎ ‎，平面BCF，‎ 平面BCF．‎ 设，，，，‎ ‎，1，，，，‎ ‎，，，‎ 设平面ABE的法向量y，，‎ 则，取，得，‎ 设平面BDE的法向量y，，‎ 则，取，得0，，‎ 设二面角的平面角为，‎ 则，二面角的余弦值为．‎ ‎19．【详解】（1）易知，因为，所以为等腰三角形．‎ 所以，由可知，故椭圆的标准方程为：．‎ ‎（2）由已知得，，设椭圆的标准方程为，P的坐标为 因为，，所以，，‎ 由题意得，所以．‎ 又因为P在椭圆上，所以，由以上两式可得 因为P不是椭圆的顶点，所以，，故 设圆心为，则，‎ 圆的半径假设存在过直线满足题设条件，并设该直线的方程为由相切可知，所以，即，解得，故存在满足条件的直线．‎ ‎20【详解】（1）函数的定义域为，，‎ 则（1），（1），‎ 故曲线在点，（1）处的切线方程为，‎ 又曲线在点，（1）处的切线方程为，‎ ‎，；‎ ‎（2）证明：由（1）知，，则，‎ 令，则，易知在单调递减，‎ 又，（1），‎ 故存在，使得，‎ 且当时，，单调递增，当，时，，单调递减，‎ 由于，（1），（2），‎ 故存在，使得，‎ 且当时，，，单调递增，当，时，，，单调递减，‎ 故函数存在唯一的极大值点，且，即，‎ 则，‎ 令，则，‎ 故在上单调递增，‎ 由于，故（2），即，‎ ‎．‎ ‎22.解　(1)曲线C的极坐标方程是ρ＝2cos θ，‎ 化为ρ2＝2ρcos θ，可得曲线C的直角坐标方程为x2＋y2－2x＝0.‎ 直线l的参数方程是(t为参数)，‎ 消去参数t可得x＝y＋m，‎ 即直线l的普通方程为y－x＋m＝0.‎ ‎(2)把(t为参数)代入方程x2＋y2＝2x，‎ 化为t2＋(m－)t＋m2－‎2m＝0，①‎ 由Δ>0，解得－10.‎ ‎∴实数m＝1±或m＝1.‎ ‎23.试题解析：（Ⅰ）由题意知，原不等式等价于 或或，‎ 解得或或，‎ 综上所述，不等式的解集为.‎ ‎（Ⅱ）当时，则 ，‎ 此时的图象与轴围成一个三角形，满足题意：‎ 当时， ，‎ 则函数在上单调递减，在上单调递增.‎ 要使函数的图象与轴围成一个三角形，‎ 则，解得；‎ 综上所述，实数的取值范围为.‎