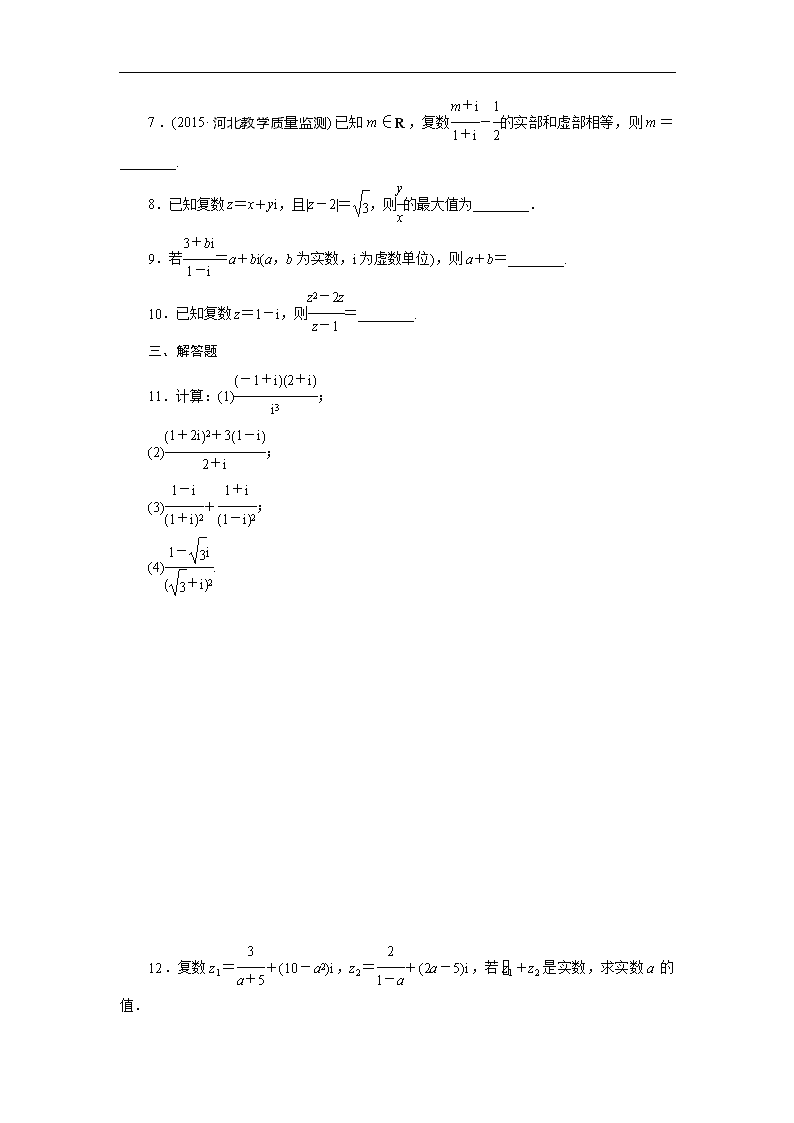2016届高考数学（理）大一轮复习达标训练试题：课时跟踪检测(二十九)　数系的扩充与复数的引入 4页

课时跟踪检测(二十九)　数系的扩充与复数的引入 一、选择题 ‎1．(2014·江西高考)若复数 z满足z(1＋i)＝2i(i为虚数单位)，则|z|＝(　　)‎ ‎ A．1　　　　　　　　　　　 B．2‎ C. D. ‎2．已知复数是纯虚数，则实数a＝(　　)‎ A．－2 B．4‎ C．－6 D．6‎ ‎3．(2015·洛阳统考)设复数z＝(i为虚数单位)，z的共轭复数为，则在复平面内i对应的点的坐标为(　　)‎ A．(1,1) B．(－1,1)‎ C．(1，－1) D．(－1，－1)‎ ‎4．若复数z＝a2－1＋(a＋1)i(a∈R)是纯虚数，则的虚部为(　　)‎ A．－ B．－i C. D.i ‎5．(2013·陕西高考)设z1，z2是复数，则下列命题中的假命题是(　　)‎ A．若|z1－z2|＝0，则＝ B．若z1＝，则＝z2‎ C．若|z1|＝|z2|，则z1·＝z2· D．若|z1|＝|z2|，则z＝z ‎6．(2015·新乡、许昌、平顶山调研)复数z1，z2满足z1＝m＋(4－m2)i，z2＝2cos θ＋(λ＋3sin θ)i(m，λ，θ∈R)，并且z1＝z2，则λ的取值范围是(　　)‎ A．[－1,1] B. C. D. 二、填空题 ‎7．(2015·河北教学质量监测)已知m∈R，复数－的实部和虚部相等，则m＝________.‎ ‎8．已知复数z＝x＋yi，且|z－2|＝，则的最大值为________．‎ ‎9．若＝a＋bi(a，b为实数，i为虚数单位)，则a＋b＝________.‎ ‎10．已知复数z＝1－i，则＝________.‎ 三、解答题 ‎11．计算：(1)；‎ ‎(2)；‎ ‎(3)＋；‎ ‎(4).‎ ‎12．复数z1＝＋(10－a2)i，z2＝＋(‎2a－5)i，若1＋z2是实数，求实数a的值．‎ 答案 ‎1．选C　法一：设z＝a＋bi(a，b∈R)，则由z(1＋i)＝2i，得(a＋bi)·(1＋i)＝2i，所以(a－b)＋(a＋b)i＝2i，由复数相等的条件得解得a＝b＝1，所以z＝1＋i，故|z|＝＝.‎ 法二：由z(1＋i)＝2i，得z＝＝＝i－i2＝1＋i，所以|z|＝＝.‎ ‎2．选D　＝，∴当a＝6时，复数为纯虚数．‎ ‎3．选C　∵z＝＝－1＋i，∴i＝i(－1－i)＝1－i，其在复平面内对应的点的坐标为(1，－1)．‎ ‎4．选A　由题意得所以a＝1，‎ 所以＝＝＝－i，根据虚部的概念，可得的虚部为－.‎ ‎5．选D　对于A，|z1－z2|＝0⇒z1＝z2⇒＝，是真命题；对于B，C易判断是真命题；对于D，若z1＝2，z2＝1＋ i，则|z1|＝|z2|，但z＝4，z＝－2＋2i，是假命题．‎ ‎6．选C　由复数相等的充要条件可得化简得4－4cos2θ＝λ＋3sin θ，由此可得λ＝－4cos2θ－3sin θ＋4＝－4(1－sin2θ)－3sin θ＋4＝4sin2 θ－3sin θ＝42－，因为sin θ∈[－1,1]，所以4sin2θ－3sin θ∈.‎ ‎7．解析：－＝－＝－＝，由已知得m＝1－m，则m＝.‎ 答案： ‎8．解析：∵|z－2|＝＝，‎ ‎∴(x－2)2＋y2＝3.‎ 由图可知max＝＝.‎ 答案： ‎9．解析：由＝＝＝a＋bi，‎ 得a＝，b＝，解得b＝3，a＝0，所以a＋b＝3.‎ 答案：3‎ ‎10．解析：＝＝z－1－＝(－i)－＝－i－＝－2i.‎ 答案：－2i ‎11．解：(1)＝＝－1－3i.‎ ‎(2)＝＝＝＝＋i.‎ ‎(3)＋＝＋＝＋＝－1.‎ ‎(4)＝ ‎＝＝ ‎＝－－i.‎ ‎12．解：1＋z2＝＋(a2－10)i＋＋(‎2a－5)i ‎＝＋[(a2－10)＋(‎2a－5)]i ‎＝＋(a2＋‎2a－15)i.‎ ‎∵1＋z2是实数，‎ ‎∴a2＋‎2a－15＝0，解得a＝－5或a＝3.‎ ‎∵a＋5≠0，∴a≠－5，故a＝3.‎