2020届二轮复习函数模型及其应用课时作业（全国通用） 8页

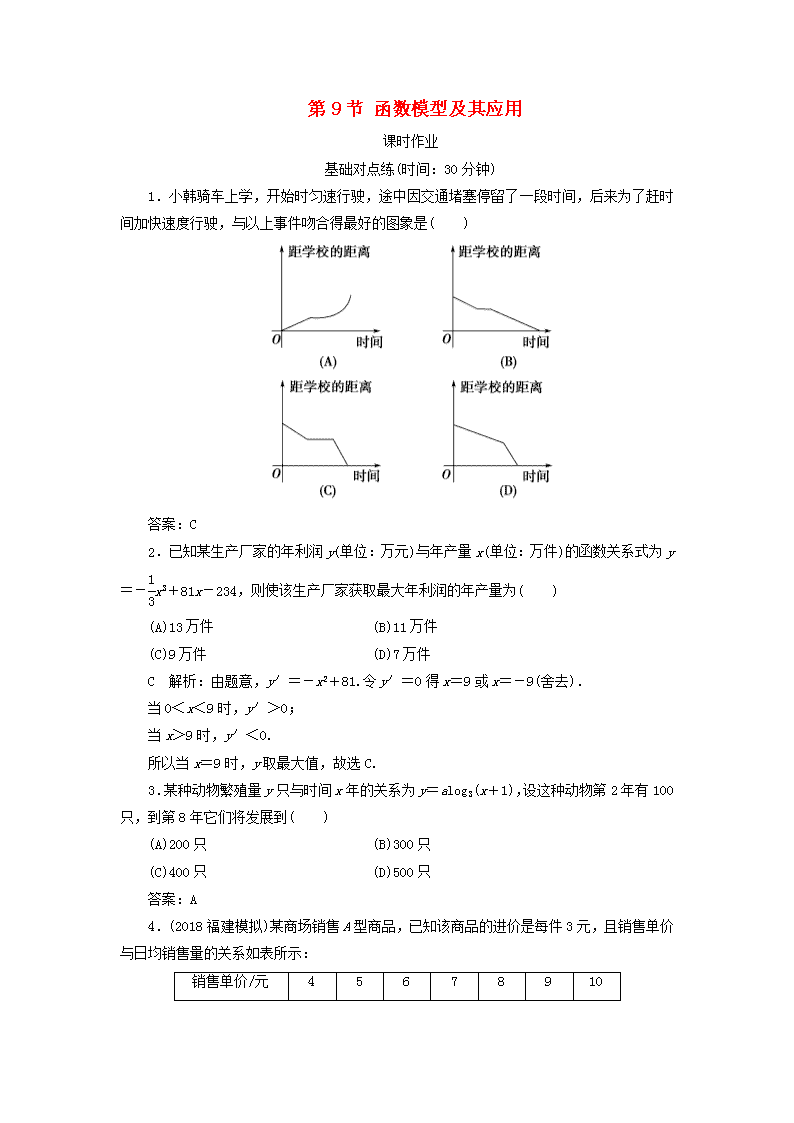
第9节 函数模型及其应用 课时作业 基础对点练(时间：30分钟)‎ ‎1．小韩骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后来为了赶时间加快速度行驶，与以上事件吻合得最好的图象是(　　)‎ 答案：C ‎2．已知某生产厂家的年利润y(单位：万元)与年产量x(单位：万件)的函数关系式为y＝－x3＋81x－234，则使该生产厂家获取最大年利润的年产量为(　　)‎ ‎(A)13万件　　　　　　　 (B)11万件 ‎(C)9万件 (D)7万件 C　解析：由题意，y′＝－x2＋81.令y′＝0得x＝9或x＝－9(舍去)．‎ 当0＜x＜9时，y′＞0；‎ 当x＞9时，y′＜0.‎ 所以当x＝9时，y取最大值，故选C.‎ ‎3．某种动物繁殖量y只与时间x年的关系为y＝alog3(x＋1)，设这种动物第2年有100只，到第8年它们将发展到(　　)‎ ‎(A)200只 (B)300只 ‎(C)400只 (D)500只 答案：A ‎4．(2018福建模拟)某商场销售A型商品，已知该商品的进价是每件3元，且销售单价与日均销售量的关系如表所示：‎ 销售单价/元 ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 日均销售量/件 ‎400‎ ‎360‎ ‎320‎ ‎280‎ ‎240‎ ‎200‎ ‎160‎ 请根据以上数据分析，要使该商品的日均销售利润最大，则此商品的定价(单位：元/件)应为(　　)‎ ‎(A)4 (B)5.5‎ ‎(C)8.5 (D)10‎ C　解析：由题意可设定价为x元/件，利润为y元，则y＝(x－3)[400－40(x－4)]＝40(－x2＋17x－42)，故当x＝8.5时，y有最大值，故选C.‎ ‎5.‎ 在如图所示的锐角三角形空地中，欲建一个面积不小于‎300 m2‎的内接矩形花园(阴影部分)，则其边长x(单位：m)的取值范围是(　　)‎ ‎(A)[15,20] (B)[12,25] ‎ ‎(C)[10,30] (D)[20,30]‎ C　‎ 解析：如图所示，过A作AG⊥BC于G，交DE于F，则＝，＝＝，又＝，‎ 所以＝，AF＝x，FG＝40－x，‎ 阴影部分的面积S＝x(40－x)≥300，‎ 解得10≤x≤30.故选C.‎ ‎6.‎ 如图，有一直角墙角，两边的长度足够长，在P处有一棵树与两墙的距离分别是a m(0